知识点三:迭代法
5.3 迭代法
迭代法是一种逐次逼近法。它是求解代数方程,超越方程及方程组的一种基本方法,但存在收敛性及收敛快慢问题。
为了用迭代法求非线性方程![]() 的近似根,首先需要将此方程转化为等价的方程
的近似根,首先需要将此方程转化为等价的方程
![]() (5.3.1)
(5.3.1)
显然,将![]() 转化为等价方程(5.3.1)的方法是很多。
转化为等价方程(5.3.1)的方法是很多。
例4 方程![]()
可用不同方法转化为等价方程:
(a)![]()
(b)![]()
定义2 (迭代法)
设方程为![]()
(1)取方程根的一个初始近似值![]() ,且按下述逐次代入法,构造一近似解序列
,且按下述逐次代入法,构造一近似解序列
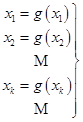 (5.3.2)
(5.3.2)
这种方法称为迭代法(或称为单点迭代法)。![]() 称为迭代函数。
称为迭代函数。
(2)果由迭代法产生序列![]() 有极限存在,即
有极限存在,即![]() 称
称![]() 收敛或称迭代过程(5.3.2)收敛。否则成
收敛或称迭代过程(5.3.2)收敛。否则成![]() 不收敛。
不收敛。
设![]() 为连续函数,且
为连续函数,且![]() ,则有
,则有![]() ,即
,即![]() 为方程(5.3.1)的解(称
为方程(5.3.1)的解(称![]() 为函数
为函数![]() 的不动点)。
的不动点)。
事实上,由迭代过程(5.3.2)两边取极限,则有
![]()
显然,在由方程![]() 转化为等价的方程
转化为等价的方程![]() 时,选择不同的迭代函数
时,选择不同的迭代函数![]() ,就会产生不同的序列
,就会产生不同的序列![]() (即使初始值
(即使初始值![]() 选择一样),且这些序列的收敛情况也不会相同。
选择一样),且这些序列的收敛情况也不会相同。
例5 对例4中的方程,考查用迭代法求根:
(a)![]()
(b)![]()
取![]() ,计算结果见表5-2.
,计算结果见表5-2.
表5-2
|
|
|
|
0 1 2 3 4 5 6 7 |
1.0 1.341471 1.473820 1.495301 1.497152 1.497289 1.497300 1.497300 |
1.0 0.523599 0.23601 -0.496555 -1.487761
|
-3.6× |
由计算看出,我们选取的两个迭代函数![]() 和
和![]() 分别构造的序列
分别构造的序列![]() 的收敛情况不一样(初始值都取为1.0),在(a)种情况下
的收敛情况不一样(初始值都取为1.0),在(a)种情况下![]() 收敛且
收敛且![]() 。在(b)种情况下出现计算
。在(b)种情况下出现计算![]() 无定义。
无定义。
因此,对于用迭代法求方程![]() 近似根需要研究下述问题:
近似根需要研究下述问题:
(1)如何选取迭代函数![]() 使迭代过程
使迭代过程![]() 收敛。
收敛。
(2)若![]() 收敛较慢时,怎样加速
收敛较慢时,怎样加速![]() 收敛。
收敛。
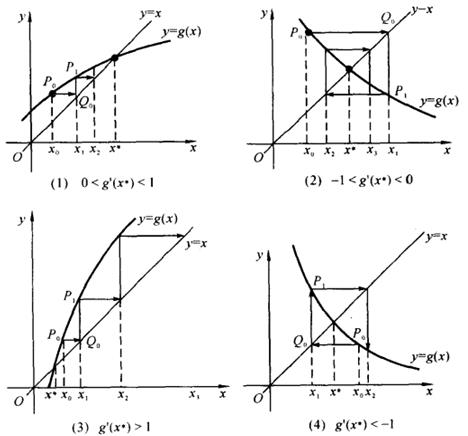
图5-3
迭代法的几何意义:
从几何上解释,求方程![]() 根的问题,是求曲线
根的问题,是求曲线![]() 与直线
与直线![]() 交点的横坐标
交点的横坐标![]() 。当迭代函数
。当迭代函数![]() 的导数
的导数![]() 在根
在根![]() 处满足下述几种条件时,从几何上来考查迭代过程
处满足下述几种条件时,从几何上来考查迭代过程![]() 的收敛情况如图5-3。
的收敛情况如图5-3。
从曲线![]() 上一点
上一点![]() 出发,沿着平行于
出发,沿着平行于![]() 轴方向前进交
轴方向前进交![]() 于一点
于一点![]() ,再从
,再从![]() 点沿平行于
点沿平行于![]() 轴方向前进交
轴方向前进交![]() 于
于![]() 点,显然,
点,显然,![]() 的横坐标就是
的横坐标就是![]() 。继续这过程就得到序列
。继续这过程就得到序列![]() ,且从几何上观察知道在(1),(2)情况下
,且从几何上观察知道在(1),(2)情况下![]() 收敛于
收敛于![]() ,在(3),(4)情况下
,在(3),(4)情况下![]() 不收敛于
不收敛于![]() 。
。
由迭代法的几何意义可知,为了保证迭代过程收敛,应该要求迭代函数的导数满足条件![]() ,当
,当![]() ,否则方程在
,否则方程在![]() 内可能有几个根或迭代法不收敛,为此有下述关于迭代法收敛性定理。
内可能有几个根或迭代法不收敛,为此有下述关于迭代法收敛性定理。
定理4 设有方程![]() 。
。
(1)设![]() 于
于![]() 一阶导数存在;
一阶导数存在;
(2)当![]() 时,有
时,有![]() ;
;
(3)![]() 满足条件:
满足条件:![]() ,当
,当![]() 。
。
则
(1)![]() 在
在![]() 有唯一解
有唯一解![]() ;
;
(2)对任意选取的初始值![]() ,迭代过程
,迭代过程![]() 收敛,即
收敛,即![]() ;
;
(3)![]() ; (5.3.3)
; (5.3.3)
(4)误差估计
![]() (5.3.4)
(5.3.4)
证明 (1)由假设条件(2)即有当![]() 时有
时有![]() 。作函数
。作函数![]() ,显然
,显然![]() 在
在![]() 上连续,
上连续,![]() 存在且满足:
存在且满足:
![]()
于是,由连续函数性质,则有![]() ,使
,使![]() ,即
,即![]() 。
。
下面证明惟一性,设有两个解![]() 及
及![]() ,且
,且![]() ,
,![]() ,即有
,即有
![]()
由中值定理有
![]()
其中,![]() 在
在![]() 与
与![]() 之间,所以
之间,所以![]() ,上式即
,上式即
![]()
又由假设条件(3)则![]() 。
。
(2)由定理假设条件(2),当取![]() 时,则有
时,则有![]() 。记误差
。记误差![]() ,由中值公式有
,由中值公式有
![]()
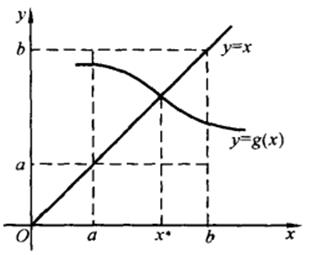
图 5-4
其中,![]() 在
在![]() 与
与![]() 之间,即
之间,即![]() 。又利用假设条件(3)得到误差的递推关系
。又利用假设条件(3)得到误差的递推关系
![]() (5.3.5)
(5.3.5)
反复利用式(5.3.5),得到
![]() (当
(当![]() )
)
即 ![]()
(3)由迭代公式![]() ,显然有
,显然有
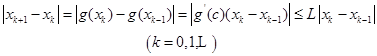 (5.3.6)
(5.3.6)
其中,![]() 在
在![]() 与
与![]() 之间,于是
之间,于是
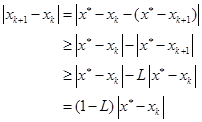
即
![]()
(4)反复利用式(5.3.6),可得
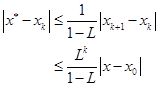
由定理4的结果(5.3.3)式可知,当计算得到的相邻两次迭代满足条件
![]() (5.3.7)
(5.3.7)
时,则误差
![]()
所以在电算时可利用![]() 来控制迭代终止,但是要注意,当
来控制迭代终止,但是要注意,当![]() 时,即使
时,即使![]() 很小,但误差
很小,但误差![]() 还可能较大。
还可能较大。
当已知![]() 及给定精度要求
及给定精度要求![]() 时,利用式(5.3.4)可确定使误差达到给定精度要求所需要的迭代次数
时,利用式(5.3.4)可确定使误差达到给定精度要求所需要的迭代次数![]() 。
。
事实上,由
![]()
即
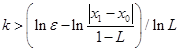 (5.3.8)
(5.3.8)
定理4的假设条件![]() ,当
,当![]() 。在一般情况下,可能对于大范围的含根区间不满足,而在根的邻近是成立的,为此有下述迭代过程局部收敛性结果。
。在一般情况下,可能对于大范围的含根区间不满足,而在根的邻近是成立的,为此有下述迭代过程局部收敛性结果。
定理5 (迭代法的局部收敛性)
设给定方程![]()
(1)设![]() 为方程的解;
为方程的解;
(2)设![]() 在
在![]() 的邻近连续可微,且有
的邻近连续可微,且有
![]()
(根据![]() 在
在![]() 邻近连续性,此条件即为存在
邻近连续性,此条件即为存在![]() 一个邻域
一个邻域![]() 使
使![]() ,当
,当![]() 时成立)。则对任意取初值
时成立)。则对任意取初值![]() ,迭代过程
,迭代过程![]() 收敛于
收敛于![]() (称迭代过程具有局部收敛性)。
(称迭代过程具有局部收敛性)。
证明 取![]() ,于是只要验证定理4中条件(2)成立,定理5即得证。
,于是只要验证定理4中条件(2)成立,定理5即得证。
事实上,设![]() ,则
,则![]()
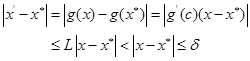
其中,![]() 。说明
。说明![]() 。
。
例6 试用迭代法解方程:![]() 。
。
解 (1)显然有
![]() 及
及![]()
即知,方程于![]() 及
及![]() 内有根,记为
内有根,记为![]() 及
及![]() 。
。
(2)考查取初值![]() 迭代过程
迭代过程![]() 的收敛性,其中迭代函数为
的收敛性,其中迭代函数为![]() 。
。
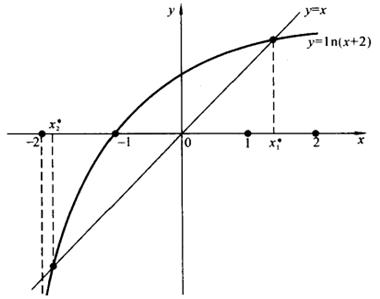
图 5-5
显然,![]() 及
及![]() 为增函数,则有当
为增函数,则有当![]() 时,
时,![]() 。又由
。又由
![]()
则有![]() 。
。
于是,由定理4可知,当初值![]() 时迭代过程
时迭代过程![]() 收敛。
收敛。
如果要求![]() 近似根准确到小数后第6位(即要求
近似根准确到小数后第6位(即要求![]() )。
)。
表5-3
|
|
0 1 2
14 15 |
0.0 0.69314718 0.99071046
1.1461931 1.1461932 |
由表5-3可知,![]() ,且
,且![]() ,所以
,所以
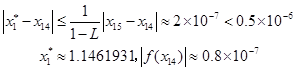
(3)可将方程转化为等价方程
![]() 或
或![]()
且有 ![]()
即有 ![]() ,
,
所以,当选取![]() 时迭代过程
时迭代过程
![]()
收敛。如取![]() ,则迭代12次有
,则迭代12次有
![]()
且有 ![]() 。
。
由上例可见,对于方程![]() ,迭代函数
,迭代函数![]() 选取不同,相应由迭代法产生的
选取不同,相应由迭代法产生的![]() 收敛情况也不一样。因此,我们应该选择迭代函数,使构造的迭代过程
收敛情况也不一样。因此,我们应该选择迭代函数,使构造的迭代过程![]() 收敛且收敛较快。
收敛且收敛较快。
迭代法框图见图5-6所示。
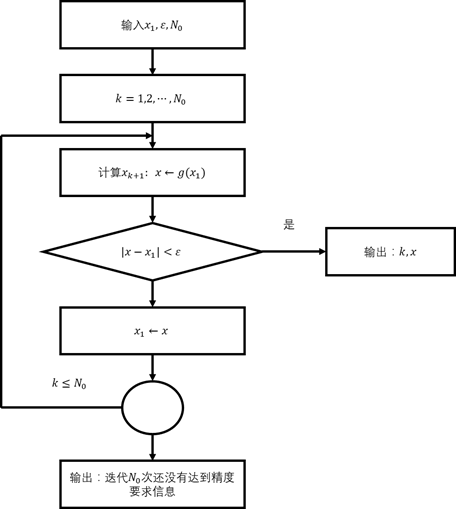
图5-6
迭代法:求解方程![]() 。
。
(1)选取解的初始估计![]() ;
;
(2)对于![]() ,计算
,计算![]() ,其中
,其中![]() 为给定的最大迭代次数。当
为给定的最大迭代次数。当![]() 时(或
时(或![]() ,或
,或![]() ,其中
,其中![]() 为给定精度要求)迭代终止。
为给定精度要求)迭代终止。
