5.4 牛顿—雷扶生方法

解非线性方程牛顿方法是一种将非线性函数线性化的方法。牛顿方法的最大优点是在方程单根附近具有较高的收敛速度，牛顿方法可用来计算的实根，还可计算代数方程的复根。

5.4.1 牛顿法公式及误差分析

设有非线性方程

                　　　（5.4.1）

其中，设为上一阶连续可微，且；又设是一个零点的近似值（设），现考虑用过曲线上点的切线近似代替函数，即用线性函数

代替，且用切线（即线性函数）的零点，记为，作为方程（5.4.1）根的近似值，即求解

得到

　　　　　　　　　　　　　　　　　　　　　　　（5.4.2）

一般，若已求得，将式（5.4.2）中的换为，重复上述过程，即得求方程根的牛顿方法的计算公式

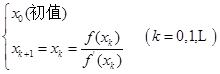　　　　　　　　　　　　　　　　　　（5.4.3）

下面利用的泰勒公式进行误差分析。设已知

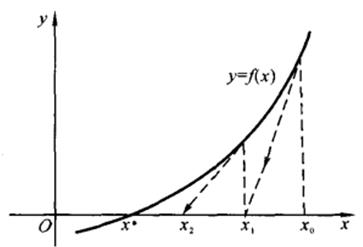
图5-7

的根的第次近似，于是在点泰勒公式为（设二次连续可微）：

           (5.4.4)

其中，在与之间。

如果用线性函数近似代替，其误差为，且用根记为作为的根的近似值又得到牛顿公式

现在式（5.4.4）中取,则有

于是（设）

利用牛顿公式（5.4.3）即得误差关系式

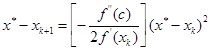               （5.4.5）

误差公式（5.4.5）说明的误差是与误差的平方成比例的。当初始误差（即）是充分小时，以后迭代的误差将非常快地减少。

由计算公式（5.4.3）可知，用牛顿方法求方程的根，每计算一步需要计算一次函数值及一次导数。

例7　用牛顿法求的根。

解   显然，，方程于内有一根。求导

牛顿法计算公式为

（1）取，计算结果见表5-4.

（2）取，计算结果见表5-5.

表5-4                   表5-5

0 1 2 3 4 5 6	1.0 －1.155999 0.189438 0.714043 0.782542 0.783595 0.783596		0 1 2	8.0 34.778107 869.1519

求得近似根，。

说明当初值选取靠近根时牛顿法收敛且收敛较快，当初值不是选取接近方程根时，牛顿法可能会给出发散的结果。

例8　对于例3试用牛顿法计算内一实根。

解   ，

牛顿法计算公式：

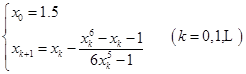
计算结果见表5-6

表5-6

方程的真根，求得的近似根具有8位有效数字。

5.4.2 牛顿法的局部收敛性

设有方程，显然，牛顿法是一种迭代法，即

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（5.4.6）

其中迭代函数为

        （设）

于是，可用迭代法理论来考查牛顿方法的收敛性。

定理6  （牛顿法的局部收敛性）

设有方程

（1）设在根邻近具有连续二阶导数；

（2）且设，但，则存在的一个邻域使得对于任意选取初值，由牛顿法产生的序列收敛于且有　　

    　　  　　　　　　　　　　 （5.4.7）

证明    由于牛顿法是一个迭代法，其迭代函数为

计算 　　

由假设条件（2），则有

于是由定理5，迭代法式（5.4.6）（即牛顿法）为局部收敛。且由（5.4.5）式取极限即得（5.4.7）式。

5.4.3 牛顿法例子及框图

例9　设，试用牛顿法建立计算的公式。

解   开方问题即为求解方程。现用牛顿法解此方程，见图5-8

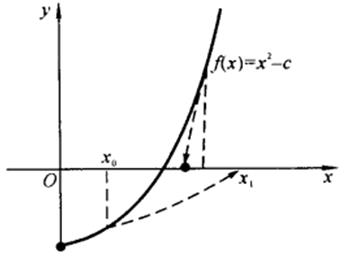
图5-8

试计算，要求时迭代终止。

取，用牛顿法计算结果见表5-7。

表5-7

所以  

例10　用牛顿法求方程

的正实根。

 

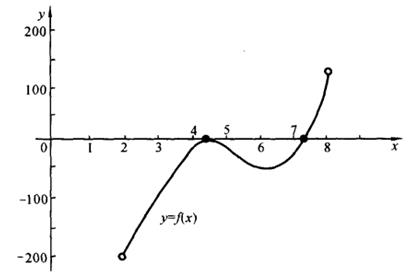
图5-9

方程在内有一实根，在内有二重根（见图5-9）。

（1）用牛顿法计算内单根，要求。计算结果见表5-8

表5-8

即为所要求的近似根。

（2）用牛顿法求内重根。计算结果见表5-9

表5-9

需要迭代19次，则有，且。

由此例可见，牛顿方法在单根附近具有较快的收敛速度（达到一定的精度所需要的迭代次数减少），而用一般牛顿法求内二重根时收敛较慢。这种情况牛顿方法可改进如下：

设为二重根（即且）。这种情况可定义一个函数

显然，为单根，于是可用牛顿法求解。

计算公式

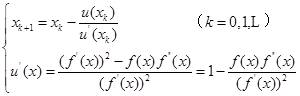    　　  　　　　  （5.4.9）

用公式（5.4.9）计算内方程的二重根，且要求，计算结果见表5-10。

表5-10

用方程（5.4.9）只迭代4次就得到满足精度要求的二重根，但这方法付出的代价是需要计算。

用牛顿方法求多项式方程复根时，初值应取为复数，即

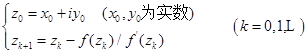
牛顿法框图见图5-10所示。

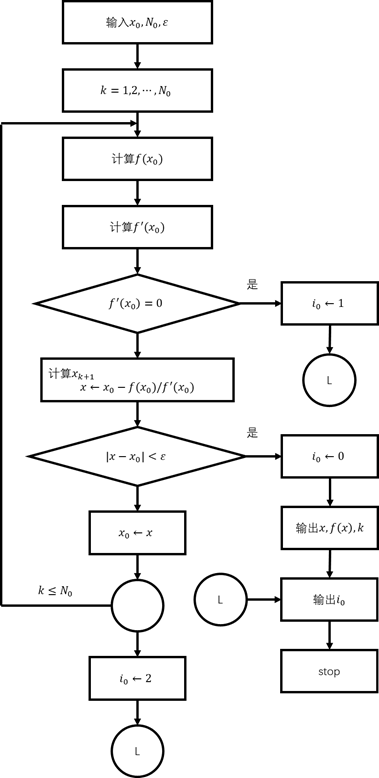
图5-10

牛顿法：设有方程。

（1）选择合适的初值；

（2），计算

其中，表示最大迭代次数，当时，迭代终止。其中，，表示求得满足给定精度的近似根；，表示，计算中断；，表示迭代次后精度要求仍不满足。

5.4.4 牛顿下山法

由牛顿迭代法的局部收敛性定理知，牛顿法对初值的要求是很苛刻的，即选取初始近似值要在根的附近，牛顿法才收敛较快，否则牛顿法产生的序列可能不收敛。但在实际应用中，往往很难给出较好的初值。牛顿下山法就是在事先没有给出较好的初值情况下，求根的一种修正的牛顿法。

为了改善对初值的要求，我们在牛顿迭代公式中引入因子，即将牛顿迭代公式修改为

其中，为初始近似值，为下山因子（可选择的参数），且满足，为下山因子下界。

选择因子（即选取）使

称为下山，将下山法和牛顿法结合使用，即牛顿下山法。

牛顿下山法计算步骤：

（1）输入，，，；

（2）计算；

（3）；

（4）计算；

（5）如果，则输出“”，停机；

（6）；

（7）计算　，

；

（8）如果，则输出，，，停机；

（9）如果，则转（11）；

（10）如果，则，转（7），否则输出“Minimum  exceeded”，停机；

（11）如果，则输出，，，停机，否则，，转（3）。

注意：其中为下山因子下界，是根的误差限，是残量精度。

例11　设方程，求在附近的一个根。

解  （1）用牛顿法计算（取）

按牛顿迭代公式计算有

，,，…

（2）用牛顿下山法计算

取，计算结果见表5-11。

表5-11

由此看出，下山法保证逐步下降，即

且牛顿法使这一过程收敛加速。