5.5 正割法和抛物线法

5.5.1 正割法

用牛顿法解非线性方程，虽然在单根邻近具有较高收敛速度，但需要计算。如果函数比较复杂，求导数可能有困难，需要更多的运算。这种情况可将牛顿法公式中的近似用差商来代替，即

于是得到计算公式：

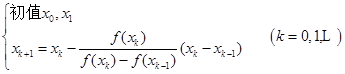　　　　　　　　　　　　　（5.5.1）

公式（5.5.1）就是正割法公式。

 

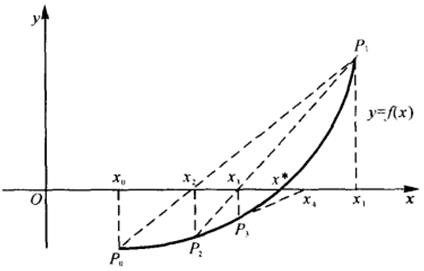
图5-11

正割法公式（5.5.1）可从下述想法得到：

设方程，且,于上连续，如果已知，，则可通过两点，用线性函数近似代替，且求的根记为作为的近似根，其中为

即为（5.5.1）式。正割法与牛顿法相比，其收敛速度较慢。

例12　用正割法求方程在内的根。

解  取初值，，计算结果见表5-12。

表5-12

0 1 2 3 4 5 6	－2 －1 －1.4 －1.499 －1.526841 －1.525079 －1.525102	－9 6 1.776000 0.389743 －0.026330 0.000348 0.000000

 

可以证明下述局部收敛定理：设。

如果，，在根某个领域上连续，且，则当取初始近似值充分接近时，由正割法产生序列收敛于且有

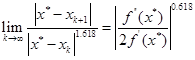                （5.5.2）

5.5.2 抛物线法(Muller法)

抛物线法是求多项式方程的实根和复根的有效方法，也可用来求一般函数方程的根。抛物线法是正割法的推广。

设有非线性方程

　　　　　　　　　　　　　　　　　　　　　　　　　　　　（5.5.2）

首先给出方程（5．5．3）根的三个初始近似值，过三个点，，，可构造二次插值多项式，用它来代替，求的根，记为作为方程根的第3次近似值，这就是抛物线法（设，，三点不共线)。

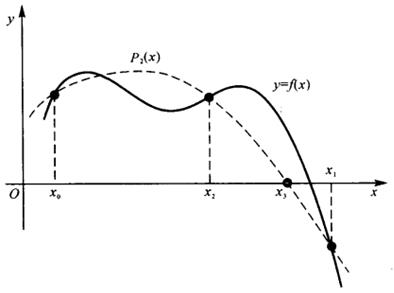
图5-12

一般情况，设已求得方程根的近似值，并用过三点构造的二次插值多项式的根，并记为作为方程根的第次近似值，见图5—12。

显然

　　　　　　　　　　(5.5.4)

其中   

          

为了求出根，将（5．5．4）式写成更加方便的形式，

即

          　　　　　　（5.5.5）

其中 　

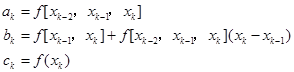
寻求的绝对值最小的根记为，于是是最接近的方程的根。

解此二次方程，得

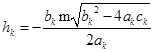
于是，初值为的抛物线法计算公式为

          （5.5.6）

其中，由（5．5．5）式求得，根式前符号应选择使（5．5．6）式分母的绝对值或模最大，即符号应取为与同号，也就是说，在的两个根中选择最接近的作为根的第次近似值。

为了计算上的方便，引入量

于是

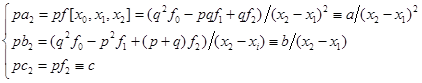 　　　　　　  （5.5.7）

将式（5．5．7）代入式（5．5．6）得到二次函数的零点为：

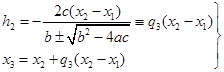　　　　　　　　　　　　　　（5.5.8）

其中   

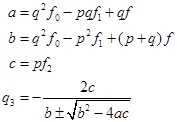
抛物线法（Muller方法）计算步骤：设方程

（1）选定三个初始近似值，计算相应的函数值，计算

（2）迭代计算

；

（按（5.5.8）式计算，且分母中“”号与取同号）；

；

计算。

（3）如果或（为给定精度），则迭代终止，即为所求，否则转（4）。

（4）如果迭代次数超过指定次数，则认为迭代过程不收敛，计算失败，否则以（）分别代替（），转（2）继续迭代。

注意：这里

例13 用抛物线法计算例12中方程的根。

解   取初始近似值，计算。

（1）计算：

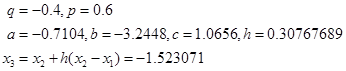
（2）计算：由

继续迭代，计算

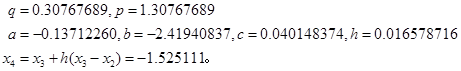
计算

上述计算结果与例12中正割法的结果比较，可知抛物线法收敛较快。

可以证明下述局部收敛定理。

如果在根邻近存在连续的三阶导数且初始近似值充分接近，则抛物线方法迭代过程是收敛的，且有

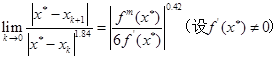 　　　　　　　 　   （5.5.9）

在抛物线方法中，即使选取为实数，但也可能是复数，所以抛物线法可适用求多项式的实根和复根。