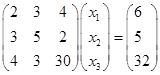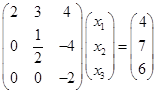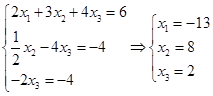当前位置:课程学习>>第六章>>知识讲解>>视频课堂>>知识点二
知识点二:高斯消去法
内容导入
高斯消去法是一个古老的求解线性方法组的方法,但由它改进得到的选主元的高斯消去法则是目前计算机上常用的解低阶稠密矩阵方程组的有效方法。
内容简介
设有![]() 个未知数的线性方程组
个未知数的线性方程组
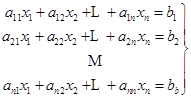
引进记号
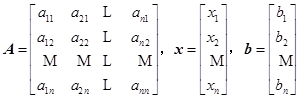
式中可用矩阵形式表示![]() ,且为了下面讨论方便,记
,且为了下面讨论方便,记![]() ,
,![]() 。假设
。假设![]() 为非奇异矩阵(即设
为非奇异矩阵(即设![]() )。
)。
第1步(![]() ):设
):设![]() 计算乘数
计算乘数
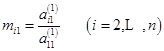
用(![]() )乘上式(6.2.1)第一个方程,加到第
)乘上式(6.2.1)第一个方程,加到第![]() 个方程上去
个方程上去![]() ,即施行行的初等变换
,即施行行的初等变换![]() ,消去第2个方程
,消去第2个方程![]() 个方程的未知数
个方程的未知数![]() ,得到式(6.2.1)的等价方程组
,得到式(6.2.1)的等价方程组
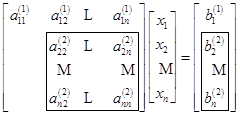
记为![]() ,其中,(6.2.3)式中的方框内元素为这一步需要计算的元素,计算公式为
,其中,(6.2.3)式中的方框内元素为这一步需要计算的元素,计算公式为
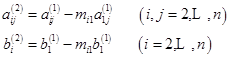
第![]() 步:
步:![]() 继续上述消去过程,设第1步~第
继续上述消去过程,设第1步~第![]() 步计算已经完成,得到与原方程组等价的方程组
步计算已经完成,得到与原方程组等价的方程组
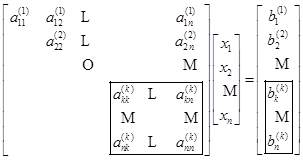
记为 ![]() 。
。
现进行第![]() 步消元计算,设
步消元计算,设![]() ,计算乘数
,计算乘数
![]()
用(![]() )乘式(6.2.4)的第
)乘式(6.2.4)的第![]() 个方程加到第
个方程加到第![]() 个方程
个方程![]() ,消去式(6.2.4)中第
,消去式(6.2.4)中第![]() 个方程
个方程![]() 的未知数
的未知数![]() ,得到与原方程组等价的方程组
,得到与原方程组等价的方程组
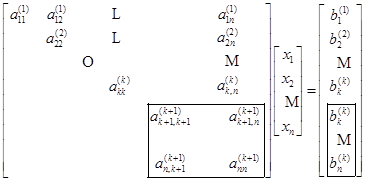
简记为![]() ,其中,
,其中,![]() 元素计算公式为
元素计算公式为
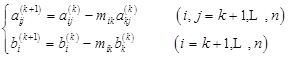
式中,![]() 与
与![]() 前
前![]() 行元素相同,
行元素相同,![]() 与
与![]() 前
前![]() 个元素相同。
个元素相同。
最后,重复上述约化过程,即![]() 且
且![]() 共完成
共完成![]() 步消元计算,得到与原方程组(6.2.1)等价的三角形方程组
步消元计算,得到与原方程组(6.2.1)等价的三角形方程组
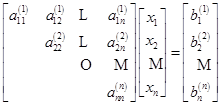
用回代的方法,即可求得方程的解,计算公式为
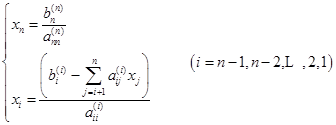
边学边练
练习题 用Gauss消去法解方程组
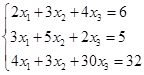
 视频学习资源下载
视频学习资源下载