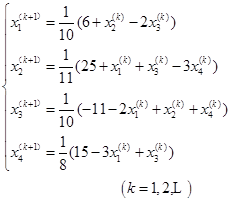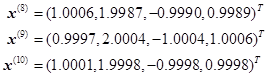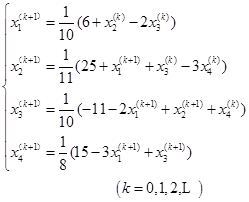当前位置:课程学习>>第六章>>知识讲解>>视频课堂>>知识点八
知识点八:解线性方程组的迭代法
内容导入
对于科学和工程中产生的大型稀疏矩阵方程组,则利用迭代法求解是合适的,迭代法在计算机内存和运算两方面通常都可利用![]() 中有大量零元素的特点。
中有大量零元素的特点。
教师解析
内容简介
设有方程组![]() ,其中
,其中![]() 为非奇异阵。解方程组的迭代法,首先需要将
为非奇异阵。解方程组的迭代法,首先需要将![]() 转化为一个等价方程组
转化为一个等价方程组![]() 。任取初始向量
。任取初始向量![]() 按下述逐次代入方法构造向量序列
按下述逐次代入方法构造向量序列![]() :
:![]() ,其中,
,其中,![]() 与
与![]() 无关,称此迭代法为一阶定常迭代法。如果
无关,称此迭代法为一阶定常迭代法。如果![]() ,则称此迭代法收敛且
,则称此迭代法收敛且![]() 为方程解。
为方程解。
![]() 为非奇异矩阵,将
为非奇异矩阵,将![]() 写为:
写为:
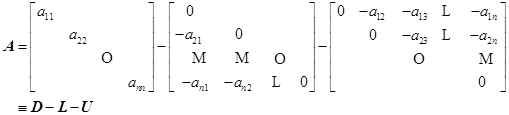
![]() 分裂为
分裂为![]() 。方程组等价与方程组
。方程组等价与方程组![]() 。构造一个迭代过程:
。构造一个迭代过程:
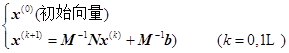
1、雅可比(Jacobi)迭代法:
选取![]() ,于是
,于是![]() ,方程的转化为等价方程组
,方程的转化为等价方程组![]() 。
。
2、高斯—塞德尔迭代法:
选取![]() (下三角矩阵),于是
(下三角矩阵),于是![]() ,方程转化为等价方程组
,方程转化为等价方程组![]() 。
。
3、解线性方程组的超松弛迭代法:
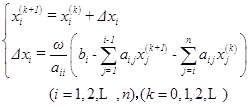
![]() 称为松弛因子
称为松弛因子
边学边练
练习题1 设有方程组

练习题2 设有方程组
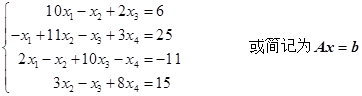
 视频学习资源下载
视频学习资源下载
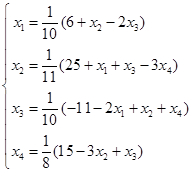 (或写为
(或写为