6.1 方程组的数值解法引言

在自然科学和工程中有很多问题的解决归结为求解线性方程组或者非线性方程组的数学问题。例如，电学中的网络问题，用最小二乘法求实验数据的曲线拟合问题，三次样条的插值问题，用有限元素法计算结构力学中的一些问题或用差分法解椭圆型偏微分方程的边值问题等等。

例1  设有电源及一些电阻组成的简单电路（图6-1），试求各环路电流。

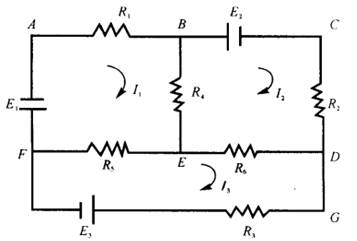
图6-1

解  设为图示的环路电流，对每一个环路，利用克希霍夫（Kirchhoff）定律：在任何一个闭合回路中，各电动势的代数和等于各电阻上电压降的代数和。

对环路：

             　　　　 ①

利用欧姆定律①式为

     　　　　　　　　　　　 ②

再用环路电流代替支路电流，即

         　　　　  ③

将③式代入②式，即得环路电流所满足代数方程

同理，对环路及环路可得方程：

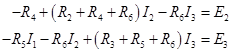
或写为矩阵形式即得到环路电流所满足的线性方程组：

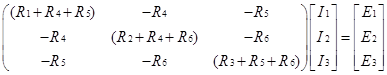
求解上述方程组，即求得环路电流。

在工程实际问题中产生的线性方程组，其系数矩阵大致有两种：一种是低价稠密矩阵（这种矩阵的全部元素都存贮在计算机的存贮器中）；另一类是大型稀疏矩阵（此类矩阵阶数高，但零元素较多，这类矩阵一般采用压缩存贮或仅存贮系数矩阵的非零元素）。