知识点二：高斯消去法
6.2 高斯消去法
高斯消去法是一个古老的求解线性方法组的方法，但由它改进得到的选主元的高斯消去法则是目前计算机上常用的解低阶稠密矩阵方程组的有效方法。
例2 用高斯消去法解方程组
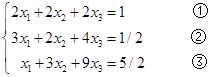
解 第1步：将方程①乘上（-3/2）加到方程②上去，将方程①乘上（-1/2）加到方程③上去，则得到与原方程组等价的方程组
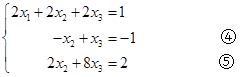
其中，方程④，⑤已消去了未知数
。
第2步：将方程④乘上2加到方程⑤，消去⑤式中未知数
，又得到与原方程组等价的三角形方程组
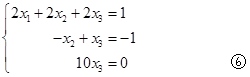
最后由上述方程组，用回代的方法，即可求得原方程组的解：
若用矩阵来描述消去法的约化过程，即为
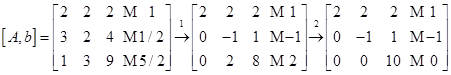
这种求解过程，称为具有回代的高斯消去法。
从这个例子看出，用高斯消去法解方程组的基本思想是用矩阵行的初等变换将系数矩阵
约化为具有简单形式的矩阵（上三角形矩阵、单位矩阵等），而三角形方程组是很容易解的。
下面讨论求解一般线性方程组的高斯消去法。设有
个未知数的线性方程组
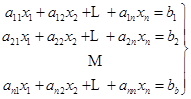（6.2.1）
引进记号
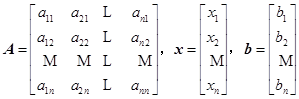
式（6.2.1）可用矩阵形式表示
（6.2.2）
且为了下面讨论方便，记
，
。假设
为非奇异矩阵（即设
）。
第1步（
）：设
计算乘数
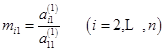
用（
）乘上式（6.2.1）第一个方程，加到第
个方程上去
，即施行行的初等变换
，消去第2个方程
个方程的未知数
，得到式（6.2.1）的等价方程组
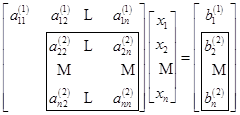（6.2.3）
记为
其中，（6.2.3）式中的方框内元素为这一步需要计算的元素，计算公式为
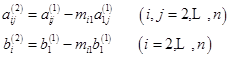
第
步：
继续上述消去过程，设第1步～第
步计算已经完成，得到与原方程组等价的方程组
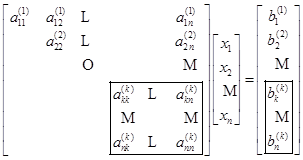（6.2.4）
记为
现进行第
步消元计算，设
，计算乘数
用（
）乘式（6.2.4）的第
个方程加到第
个方程
，消去式（6.2.4）中第
个方程
的未知数
,得到与原方程组等价的方程组
（6.2.5）
简记为
其中，
元素计算公式为
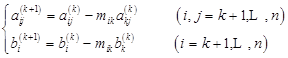（6.2.6）
式中，
与
前
行元素相同，
与
前
个元素相同。
最后，重复上述约化过程，即
且
共完成
步消元计算，得到与原方程组（6.2.1）等价的三角形方程组
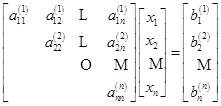（6.2.7）
用回代的方法，即可求得方程（6.2.7）的解，计算公式为
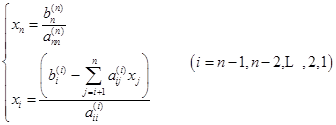（6.2.8）
元素
称为约化的主元素。将方程（6.2.1）约化为方程（6.2.7）的过程称为消元过程，方程（6.2.7）求解过程方程（6.2.8）称为回代过程，由消元过程和回代过程求解线性方程组的方法称为高斯消去法。
定理1 （高斯消去法）
设
，其中
。如果约化的主元素
，即可通过高斯消去法（不进行交换两行的初等交换）将方程组
约化为三角形矩阵方程组（6.2.7）且消元和求解公式为：
- 消元计算
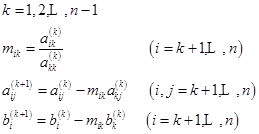
（2）回代计算
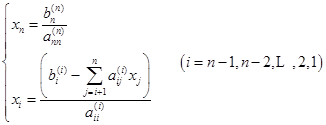
如果
为非奇异矩阵时，但可能有某
，则在第
列存在有元素
，于是可能通过交换
的第
行和第
行元素将
调到
位置，然后再进行消元计算。于是，在
为非奇异矩阵时，只要引进行交换，则高斯消去法可将
约化为三角形方程组（6.2.7），且通过回代即可求得方程组解。
高斯消去法的计算量：
（1）消元计算：第
步
。
①计算乘数：需要作
次除法运算；
②消元：需做
次乘法运算；
③计算
：需做
次乘法运算。
于是完成全部消元计算共需要作
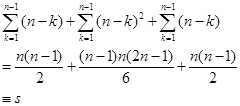
次乘除法运算。
（2）回代计算：共需要作
次乘除法运算。
于是，用高斯消去法解
的计算量为共需作
（6.2.9）
次乘除法运算。
下面比较用高斯消去法和用克莱姆（Cramer）法则解20阶方程组的计算量。、
表6-1
方法 |
高斯消去法 |
Cramer法则 |
计算量 |
3060次乘除法 |
大约5×10 |
如果计算工作是在每秒作
次乘除法的计算机上进行的，那么用高斯消去法解20阶方程组约需要0.03秒时间即可完成，而用克莱姆法则大约需
小时才能完成（大约相当于107年）。由此可知克莱姆法则完全不适用在计算机上求解高维方程组。
在计算机上用高斯消去法解低阶稠密矩阵线性方程组时要注意几点：
（1）要用一个二维数组
存放系数矩阵
的元素，用一维数组
存放常数项b分量。
（2）需要输入数据
。
（3）约化的中间结果
元素冲掉
元素，
冲掉
，乘数
冲掉
。例如，计算
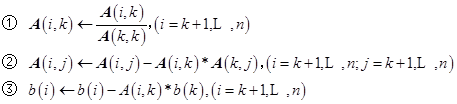
（4）在高斯消去法中一般要引进行交换。
（5）如果不存在
，使
,要输出方程组没有惟一解的信息。
