知识点三:选主元素的高斯消去法
6.3 选主元素的高斯消去法
用高斯消去法解![]() 时,其中设
时,其中设![]() 为非奇异矩阵,可能出现
为非奇异矩阵,可能出现![]() 情况,这时必须进行带行交换的高斯消去法。但在实际计算中即使
情况,这时必须进行带行交换的高斯消去法。但在实际计算中即使![]() 但其绝对值很小时,用
但其绝对值很小时,用![]() 作除数,会导致中间结果矩阵
作除数,会导致中间结果矩阵![]() 元素数量级严重增长和舍入误差的扩散,使得最后的计算结果不可靠。
元素数量级严重增长和舍入误差的扩散,使得最后的计算结果不可靠。
例3 设有方程组
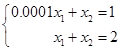
解 精确解为![]() 。
。
[方法1] 用高斯消去法求解(用具有舍入的3位浮点数进行计算)。
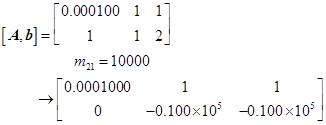
回代得到计算解![]() 。与精确解比较,这是一个很坏的结果。
。与精确解比较,这是一个很坏的结果。
[方法2] 用具有行交换的高斯消去法(避免小主元)。
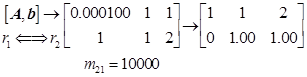
回代求解![]() 。对于用具有舍入的3位浮点数进行运算,这是一个很好的计算结果。
。对于用具有舍入的3位浮点数进行运算,这是一个很好的计算结果。
方法1计算失败的原因,是用了一个绝对值很小的数作除数,乘数很大,引起的约化中间结果数量级严重增长,再舍入就使得计算结果不可靠了。
这个例子告诉我们,在采用高斯消去法解方程组时,小主元可能导致计算失败,故在消去法中应避免采用绝对值很小的主元素。对一般矩阵方程组,需要引进选主元的技巧,即在高斯消去法的每一步应该在系数矩阵或消元后的低阶矩阵中选取绝对值最大的元素作为主元素,保持乘数 ![]() ,以便减少计算过程中舍入误差对计算解的影响。
,以便减少计算过程中舍入误差对计算解的影响。
这个例子还告诉我们,对同一数值问题,用不同的计算方法,得到的结果的精度大不一样。对于一个计算方法来说,如果在用此方法的计算过程中舍入误差能得到控制,对计算结果影响较小,则称此方法为数值稳定的;否则,如果在用此计算方法的计算过程中舍入误差增长迅速,计算结果受舍入误差影响较大,则称此方法为数值不稳定。因此,我们解数值问题时,应选择和使用数值稳定的计算方法,否则,如果使用数值不稳定的计算方法去解数值问题,就可能导致计算失败。
6.3.1 完全主元素消去法
设有线性方组![]() ,其中
,其中![]() 为非奇异矩阵。方程组的增广矩阵为
为非奇异矩阵。方程组的增广矩阵为
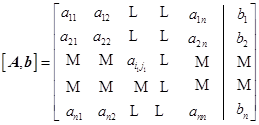
第1步(![]() ):首先在
):首先在![]() 中选主元素,即选择
中选主元素,即选择![]() 使
使
![]()
再交换![]() 的第1行与第
的第1行与第![]() 行元素,交换
行元素,交换![]() 的第1列与第
的第1列与第![]() 列元素(相当于交换未知数
列元素(相当于交换未知数![]() 与
与![]() ),将
),将![]() 调到(1,1)的位置(交换后增广矩阵为简单起见仍记为
调到(1,1)的位置(交换后增广矩阵为简单起见仍记为![]() ,其元素仍记为
,其元素仍记为![]() ,
,![]() )。然后,进行消元计算。
)。然后,进行消元计算。
第![]() 步:继续上述过程,设已完成第1步到第
步:继续上述过程,设已完成第1步到第![]() 步计算。
步计算。![]() 约化为下述形式(为简单起见,仍记
约化为下述形式(为简单起见,仍记![]() 元素为
元素为![]() ,
,![]() 元素为
元素为![]() ):
):
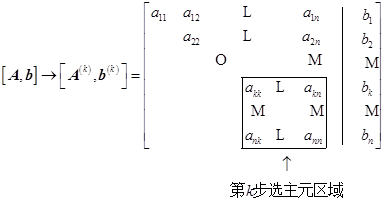
于是第![]() 步计算:
步计算:
对于![]() 做到(3)。
做到(3)。
(1)选主元素:选取![]() ,使
,使
![]()
(2)如果![]() ;则交换
;则交换![]() 第
第![]() 行与第
行与第![]() 行元素,如果
行元素,如果![]() ,则交换
,则交换![]() 的第
的第![]() 列与第
列与第![]() 列元素。
列元素。
(3)消元计算:
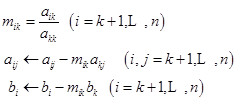
(4)回代求解。
经过上面的过程,即从第1步到![]() 步完成选主元,交换两行,交换两列,消元计算,原方程组约化为
步完成选主元,交换两行,交换两列,消元计算,原方程组约化为
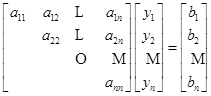
其中,![]() 为未知数
为未知数![]() 调换后的次序。回代求解
调换后的次序。回代求解
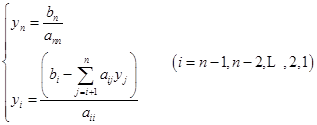
6.3.2 列主元素消去法
完全主元消去法是解低阶稠密矩阵方程组的有效方法,但完全主元消去法在选主元时要花费一定的计算机时间。现介绍一种在实际计算中常用的部分选主元(即列主元)消去法。列主元消去法即是每次选主元时,仅依次按列选取绝对值最大的元素作为主元素,且仅交换两行,再进行消元计算。
设列主元消去法已经完成第1步到第![]() 步的按列选主元,交换两行,消元计算得到与原方程组等价的方程组
步的按列选主元,交换两行,消元计算得到与原方程组等价的方程组
![]()
其中
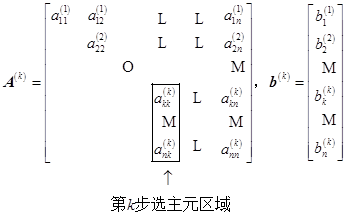
第![]() 步计算如下:
步计算如下:
对于![]() 做到(4)。
做到(4)。
(1)按列选主元,即确定![]() 使
使
![]()
(2)如果![]() ,则
,则![]() 为奇异矩阵,停止计算。
为奇异矩阵,停止计算。
(3)如果![]() ,则交换
,则交换![]() 第
第![]() 行与第
行与第![]() 行元素。
行元素。
(4)消元计算:
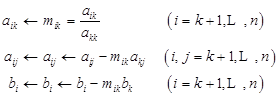
(5)回代计算:
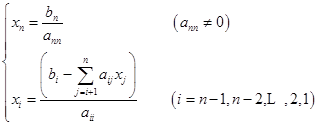
计算解![]() 在常数项
在常数项![]() 内得到,且有
内得到,且有![]() 。
。
例3的方法2就是列主元消去法。
列主元消去法框图见图6-1所示。

图6-1
用列主元消去法解![]() ,系数阵
,系数阵![]() 存放在二维数组
存放在二维数组![]() 内,常数项
内,常数项![]() 存放在
存放在![]() 内,计算解存放在
内,计算解存放在![]() 内,
内,![]() 存放在单元det内。
存放在单元det内。
