知识点四:矩阵的三角分解
6.4 矩阵的三角分解
现用矩阵理论来研究高斯消去法,设约化主元素![]() 。由于对
。由于对![]() 施行行的初等变换相当于用初等矩阵左乘
施行行的初等变换相当于用初等矩阵左乘![]() ,于是高斯消去法第1步:
,于是高斯消去法第1步:
![]()
则有
![]()
其中
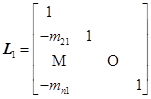 (为初等下三角阵)
(为初等下三角阵)
第![]() 步消元过程:
步消元过程:
![]()
则有
![]() (6.4.1)
(6.4.1)
其中
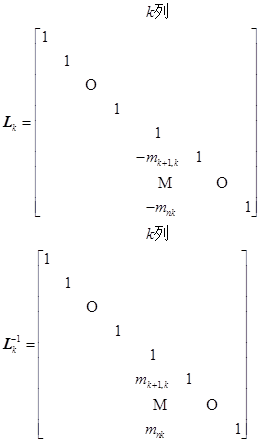
利用递推公式(6.4.1),则有
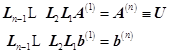 (6.4.2)
(6.4.2)
由(6.4.2)式得到
![]() (6.4.3)
(6.4.3)
其中
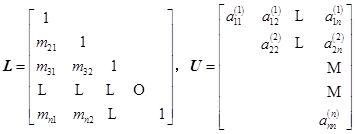
![]() 为由乘数构成的单位下三角阵,
为由乘数构成的单位下三角阵,![]() 为上三角阵,(6.4.3)式表明,用矩阵理论来分析高斯消去法,得到一个重要结果,即在
为上三角阵,(6.4.3)式表明,用矩阵理论来分析高斯消去法,得到一个重要结果,即在![]() 的条件下,高斯消去法实质上是将
的条件下,高斯消去法实质上是将![]() 分解为两个三角矩阵的乘积
分解为两个三角矩阵的乘积![]() 。
。
显然,如果![]() ,由高斯消去法的(6.2.4)式及行列式性质,则有
,由高斯消去法的(6.2.4)式及行列式性质,则有
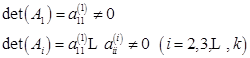
其中
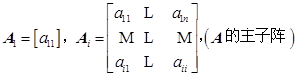
反之,可用归纳法证明,如果![]() 的顺序主子式
的顺序主子式![]() ,则
,则![]() 。
。
总结上述讨论,得到下述重要定理:
定理2(矩阵的三角分解)
设![]() 。如果
。如果![]() 的顺序主子式
的顺序主子式![]() ,则
,则![]() 可分解为一个单位下三角阵与一个上三角阵的乘积,即
可分解为一个单位下三角阵与一个上三角阵的乘积,即
![]()
且分解是惟一的。
证明 现仅就![]() 来证明惟一性。设有
来证明惟一性。设有
![]() (6.4.4)
(6.4.4)
其中,![]() 为单位下三角阵,
为单位下三角阵,![]() 为上三角阵。
为上三角阵。
由假设![]() 存在,于是从上式(6.4.4)可得
存在,于是从上式(6.4.4)可得
![]()
上式右边为上三角阵,左边为单位下三角阵,故应为单位阵,即![]() 。
。
称矩阵的三角分解![]() 为杜利特尔(Doolittle)分解。其中
为杜利特尔(Doolittle)分解。其中
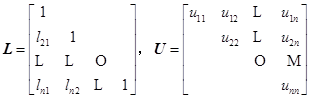
在定理2条件下,同样可有三角分解
![]()
其中,![]() 为下三角阵,
为下三角阵,![]() 为单位上三角阵。称矩阵的这种分解为克劳特(Crout)分解。
为单位上三角阵。称矩阵的这种分解为克劳特(Crout)分解。
例4 由例2可以得到![]() 的三角分解
的三角分解
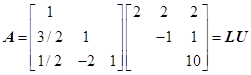
设有方程组![]() 。如果实现了
。如果实现了![]() ,则求解问题
,则求解问题
![]()
即 ①![]() ,求解
,求解![]()
②![]() ,求解
,求解![]()
求解两个三角形方程组是容易的。
在定理2条件下,用高斯消去法可以实现![]() 的三角分解
的三角分解![]() ,下面可通过直接用
,下面可通过直接用![]() 元素计算矩阵
元素计算矩阵![]() 的三角分解矩阵
的三角分解矩阵![]() 及
及![]() 。这种直接计算
。这种直接计算![]() 的三角分解的方法有实用上的好处。
的三角分解的方法有实用上的好处。
设![]() 且各顺序主子式
且各顺序主子式![]() ,于是由定理2有
,于是由定理2有
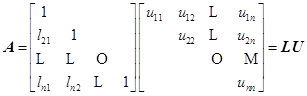 (6.4.5)
(6.4.5)
由矩阵乘法有:
![]() ,得到
,得到![]() 的第1行元素;
的第1行元素;
![]() ,得到
,得到![]() 的第1列元素。
的第1列元素。
设已经定出![]() 的第
的第![]() 行元素,
行元素, ![]() 的第
的第![]() 列元素,现要计算
列元素,现要计算![]() 的第
的第![]() 行元素及
行元素及![]() 的第
的第![]() 列元素。
列元素。
由(6.4.5)式,用矩阵乘法可得
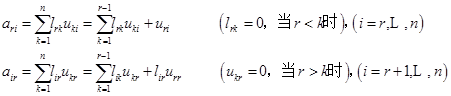
由上述讨论,得到用直接三角分解法解![]() 的计算公式。
的计算公式。
![]() 的
的![]() 分解的直接计算公式:
分解的直接计算公式:
(1)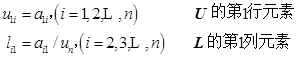
(2)对于![]() 计算:
计算:
① 计算![]() 的第
的第![]() 行元素
行元素
![]()
② 计算![]() 的第
的第![]() 列元素
列元素![]()
![]()
(3)求解![]() 公式:
公式:
①
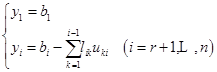
②
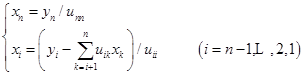
显然,当![]() 时,解
时,解![]() 直接三角分解法计算才能完成。设
直接三角分解法计算才能完成。设![]() 为非奇异矩阵,当某
为非奇异矩阵,当某![]() 时,可引用矩阵的行交换,可实现矩阵的三角分解。
时,可引用矩阵的行交换,可实现矩阵的三角分解。
用直接三角分解法解![]() 大约需要
大约需要![]() 次乘除法。
次乘除法。
在电算时,当![]() 计算好后就冲掉
计算好后就冲掉![]() 计算好后冲掉
计算好后冲掉![]() ,最后在
,最后在![]() 位置得到
位置得到![]() 。
。
用直接分解法求解方程组
![]()
是有好处的。
(1)实现分解计算![]()
(2)求解![]()
对于![]()
① 求解![]()
② 求解![]()
且每求解一个方程组![]() 只需
只需![]() 次乘除法。
次乘除法。
例5 用列主元素消去法解
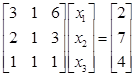
解 消元中间结果冲掉![]() 元素
元素![]() ,乘数
,乘数![]() 冲掉
冲掉![]() ,按列选主元,引进行交换时将乘数也交换。
,按列选主元,引进行交换时将乘数也交换。
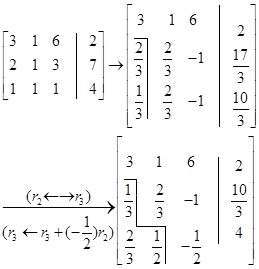
其中![]() ,且作第2行与第3行的交换,
,且作第2行与第3行的交换,![]() 。
。
解三角形的方程组
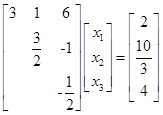
得到计算解
![]()
且有置换矩阵![]() (为初等置换阵的乘积,即
(为初等置换阵的乘积,即![]() ,其中
,其中![]() 为单位矩阵
为单位矩阵![]() 交换第
交换第![]() 行与第
行与第![]() 行得到的矩阵)使得
行得到的矩阵)使得
![]()
其中

上述例子说明,列主元素消去解![]() (假设
(假设![]() 为非奇异矩阵)实现了
为非奇异矩阵)实现了![]() 的三角分解。进一步可以证明下述结果。
的三角分解。进一步可以证明下述结果。
定理3 (列主元素三角分解定理)
如果![]() 为非奇异矩阵,则存在置换阵
为非奇异矩阵,则存在置换阵![]() 使
使
![]()
其中,![]() 为单位下三角阵,
为单位下三角阵,![]() 为上三角阵。
为上三角阵。
电算时,置换阵![]() 可用一整型数组
可用一整型数组![]() 表示(记录主行),由单位阵
表示(记录主行),由单位阵![]() 第
第![]() 行和第
行和第![]() 行互换得到
行互换得到![]() (当
(当![]() )。
)。
