6.5 解三对角线方程组的追赶法

在一些实际问题中，如用三次样条函数的插值问题，用差分法解二阶线性常微分方程边值问题等，最后都导致解三对角线方程组，即

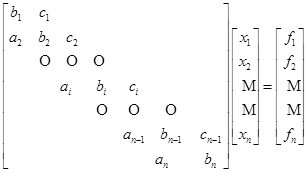   　       (6.5.1)

其中，满足条件

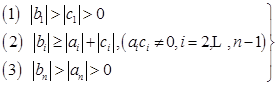　　　　      　　(6.5.2)

对于具有条件（6.5.2）的方程组（6.5.1），我们介绍下述的追赶法求解。追赶法具有计算量少、方法简单、算法稳定等特点。

定理4　设有三对角线方程组，且满足条件（6.5.2），则为非奇异矩阵。

证明  用归纳法证明，显然，对时有

现设定理对阶满足条件（6.5.2）的三对角阵成立，求证对满足条件（6.5.2）的阶三对角阵定理亦成立。由设，则由消去法一步，有

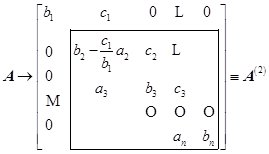
显然

其中

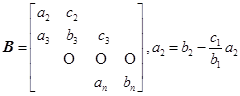
且有

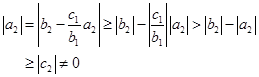
于是由归纳法假设，有，故

定理5 设，其中为满足条件（6.5.2）的三对角阵，则的所有顺序主子式都不为零，即

证明　由于是满足（6.5.2）的阶三对角阵，因此，的任一个顺序主子阵亦是满足（6.5.2）的阶三对角阵，由定理4，则有。于是，由矩阵的三角分解定理，则有

即

由矩阵乘法，可得计算待定系数的计算公式，即

（1）；

（2）

于是，；

（3）。

于是，得到解（6.5.1）的追赶法计算公式。

1. 分解计算公式

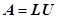
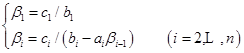
求解求解①求 ②求

（2）解的递推公式

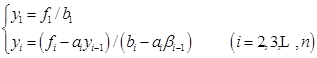
（3）求解的递推公式

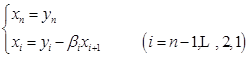
计算及的过程称为追的过程，计算方程组解的过程称为赶的过程。追赶法解，仅需要次乘除运算。

电算时，只需要用3个一维数组分别存贮的系数且还需要用两个一维数组保存计算的中间结果和（或）。

例6　用追赶法解方程组

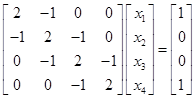
解（1）计算

（2）计算

（3）计算