6.6 解对称正定矩阵方程组的平方根法

在工程技术问题中，例如用有限元方法解结构力学中问题时，常常需要求解具有对称正定矩阵的方程组，对于这种具有特殊性质系数的矩阵，利用矩阵的三角分解法求解就得到解对称正定矩阵方程组的平方根法。平方根法是解对称正定矩阵方程组的有效方法，目前在计算机上被广泛应用。

设有方程组

                     （6.6.1）

其中，,若满足下述条件，称为对称正定矩阵。

(1) 对称，即。

(2) 对任意非零向量，则有。

对称正定矩阵具有性质：

① 设为对称正定阵，则的顺序主子式都大于零，即。

② 的特征值 。

设为对称正定矩阵，则有三角分解

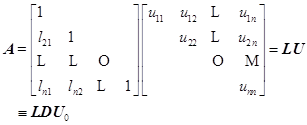        （6.6.2）

其中

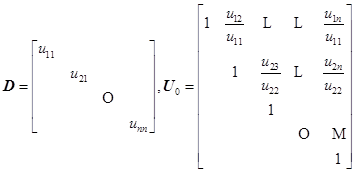
设，于是,为单位下三角阵 ，为上三角阵 ，由矩阵三角分解的唯一性，则，从而对称正定矩阵有惟一分解式

（6.6.3）

由（6.6.2）式可知

又因为,故。于是，对角阵还可分解

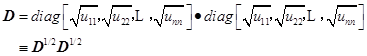
代入（6.6.3式），则有

其中，为下三角阵。

定理6  （对称正定阵的三角分解）

设为阶对称正定矩阵，则有三角分解（且惟一）：

①，其中为单位下三角阵，为对角阵，或 ②，其中为下三角阵且当限定的对角元素为正时这种分解是惟一的。这种矩阵分解称为乔来斯金（Cholesky）分解。

下面推导实现分解计算的递推公式及求解公式。

设有,其中为对称正定阵，于是有三角分解

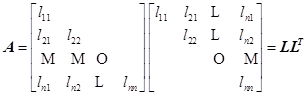
其中。

由矩阵乘法，则有

由此可确定的第1列元素。

同理，可确定L的第列元素。

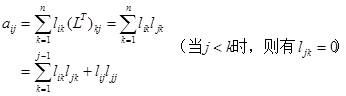
由此求得解对称正定矩阵方程组的平方根法计算公式。

(1)分解计算

 ①；

 ②对于

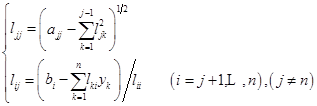
(2)求解

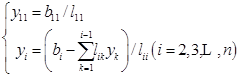
(3)求解

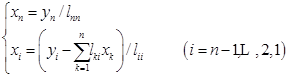
平方根法仅需计算与，因此平方根法的计算量约为次乘除法运算，大约为一般高斯消去法计算量的一半。

由分解公式有

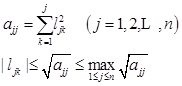           　　　　 (6.6.4)

（6.6.4 ）式说明解的平方根法所得的中间数据是有界的，即数量级不会增长。因此，虽然解对称正定矩阵方程组的平方根法没有进行选主元素，但平方根法是数值稳定的。

因为为对称矩阵，因此，电算时只需用一维数组存贮的对角线以下元素，即

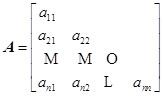
用一维数组按行存贮：

且矩阵的元素在一维数组中表示为

计算得到元素存放在的对应位置。

例7　用平方根法解方程组

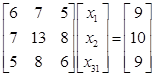
解  精确解

（1）分解计算

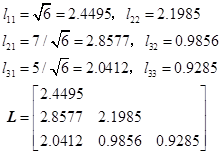
（2）求解两个三角形的方程组，求解

得到   

 

求解，即得的解

如果采用对称正定矩阵分解公式，可得到没开方运算的计算公式。