知识点七:向量和矩阵的范数
6.7 向量和矩阵的范数
为了对方程组的计算解进行误差分析,为了讨论迭代法的收敛性,需要对![]() (
(![]() 维列向量空间)中向量及
维列向量空间)中向量及![]() 中矩阵引进某种度量,即引进向量或矩阵的范数概念。
中矩阵引进某种度量,即引进向量或矩阵的范数概念。![]() 中向量范数是
中向量范数是![]() 中向量长度概念的推广。
中向量长度概念的推广。
定义1 (向量范数)
如果向量![]() 的某个实值函数
的某个实值函数![]() 满足条件:
满足条件:
(1)正定条件:![]() ,且
,且![]() 是
是![]() 向量。
向量。
(2)齐次性:![]() ,
,![]() 为实数。
为实数。
(3)三角不等式:![]() ,对任意向量
,对任意向量![]() ;
;
称![]() 是
是![]() 上的一个向量范数(或向量的模)。
上的一个向量范数(或向量的模)。
(4)利用三角不等式可推得
![]()
![]() 中三角不等式,即为两边之和大于第三边。
中三角不等式,即为两边之和大于第三边。
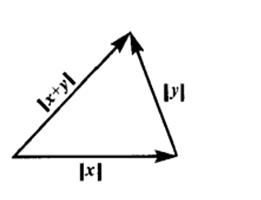
图 6-2
定义2 设![]() ,定义
,定义![]() 上三种常用的向量范数:
上三种常用的向量范数:
(1)向量的“1”范数 ![]()
(2)向量的“∞”范数 ![]()
(3)向量的“2”范数 ![]()
容易验证 ,上述定义的向量![]() 函数
函数![]() ,
,![]() 满足定义1的3个条件,因此,
满足定义1的3个条件,因此,![]() 是
是![]() 上向量的范数。
上向量的范数。
例8 设![]() ,计算
,计算![]() 。
。
解
![]()
![]()
![]()
定义3 (向量序列的极限)
设![]() 为向量序列,记为
为向量序列,记为![]() ,及
,及![]() 。如果
。如果![]() 个数列极限存在,且
个数列极限存在,且![]() ,则称
,则称![]() 收敛于
收敛于![]() ,且记
,且记![]() 。
。
定理7 设![]() 是
是![]() 中一向量序列,且
中一向量序列,且![]() ,则
,则
![]()
证明 只就![]() 证明。
证明。
显然有
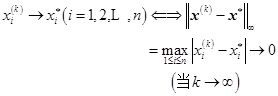
定义4 (矩阵的范数)
如果矩阵![]() 的某个非负实值函数
的某个非负实值函数![]() 满足下述条件:
满足下述条件:
(1) 正定性:![]() ,且
,且![]() 矩阵;
矩阵;
(2) 齐次性:![]() ,
,![]() 为实数;
为实数;
(3) 三角不等式:![]() ,对任意矩阵
,对任意矩阵![]() ;
;
(4) ![]() ,称
,称![]() 是
是 ![]() 上一个矩阵范数(或称为模)。
上一个矩阵范数(或称为模)。
在大多数应用问题中,矩阵和向量是有关系的,下面借助于向量范数来定义矩阵范数。
定义5 (矩阵的算子范数)
设 ![]() ,且给出一种向量范数
,且给出一种向量范数![]() ,相应地定义一个矩阵的非负函数
,相应地定义一个矩阵的非负函数![]() ,即
,即
![]() (最大比值) (6.7.1)
(最大比值) (6.7.1)
显然,由(6.7.1)式对任意![]() 有
有
![]() (6.7.2)
(6.7.2)
且容易验证![]() 满足矩阵范数条件
满足矩阵范数条件![]() ,所以
,所以![]() 是
是 ![]() 上矩阵的范数,称为
上矩阵的范数,称为![]() 的算子范数。
的算子范数。
下面验证条件(3) 成立。事实上,利用向量范数的三角不等式及 (6.7.2) 则有
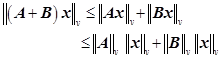
设![]() ,故有
,故有
![]()
于是 ![]()
下面给出![]() 时的向量范数,来推导矩阵算子范数
时的向量范数,来推导矩阵算子范数![]() 的计算公式。
的计算公式。
定理8 (矩阵范数计算公式)
设![]() ,则
,则
(1) ![]() 对应
对应![]() (称为
(称为![]() 的列范数);
的列范数);
(2)![]() 对应
对应![]() (称为
(称为![]() 的列范数)。
的列范数)。
证明 只证(2),同理可证(1)。
设![]() 且设
且设![]() ,引进记号
,引进记号
![]()
于是
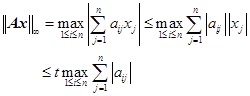
即对任何非零向量![]() ,则有
,则有
![]()
下面说明存在![]() ,使比值
,使比值![]() 。
。
事实上,选取向量![]() 为
为
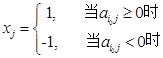
且有![]() ,
,![]() 的第
的第![]() 个向量为
个向量为
![]()
故
![]()
即 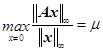
例9 设![]() ,计算
,计算![]() 。
。
解
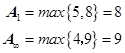
定理9 如果![]() ,则
,则![]() 为非奇异阵,且有估计
为非奇异阵,且有估计
![]()
![]() 是矩阵的算子范式。
是矩阵的算子范式。
证明 反证法,如果![]() ,则齐次方程组
,则齐次方程组![]() 有非零解
有非零解![]() ,即
,即![]() 且
且![]() ,于是有
,于是有
![]()
故有![]() ,此与假设矛盾。
,此与假设矛盾。
由![]() ,于是
,于是
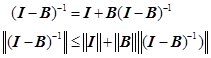
所以 ![]()
