知识点八:解线性方程组的迭代法
6.8 解线性方程组的迭代法
前面我们介绍了解线性方程组的直接法(例如选主元的高斯消去法等),但是对于科学和工程中产生的大型稀疏矩阵方程组,则利用迭代法求解是合适的,迭代法在计算机内存和运算两方面通常都可利用![]() 中有大量零元素的特点。
中有大量零元素的特点。
设有方程组![]() ,其中
,其中![]() 为非奇异阵。解方程组的迭代法,首先需要将
为非奇异阵。解方程组的迭代法,首先需要将![]() 转化为一个等价方程组
转化为一个等价方程组
![]() (6.8.1)
(6.8.1)
任取初始向量![]() 按下述逐次代入方法构造向量序列
按下述逐次代入方法构造向量序列![]() :
:
![]() (6.8.2)
(6.8.2)
其中,![]() 与
与![]() 无关,称此迭代法为一阶定常迭代法。如果
无关,称此迭代法为一阶定常迭代法。如果![]() ,则称此迭代法收敛且
,则称此迭代法收敛且![]() 为方程(6.8.1)解。事实上,在方程(6.8.2)式两边取极限即可知。
为方程(6.8.1)解。事实上,在方程(6.8.2)式两边取极限即可知。
例10 设有方程组
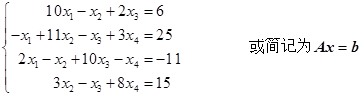
解 精确解 ![]()
首先将![]() 转化为等价方程组
转化为等价方程组
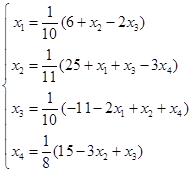 (或写为
(或写为![]() )
)
迭代公式:初始向量![]()
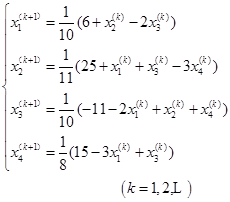
计算结果见表6-2
表6-2
|
|
|
|
|
|
0.0 |
0.6000 |
1.0473 |
0.9326 |
|
0.0 |
2.2727 |
1.07159 |
2.0533 |
|
0.0 |
-1.100 |
-0.8052 |
-1.0493 |
|
0.0 |
1.8750 |
0.8852 |
1.1309 |
|
|
|
|
|
|
1.0152 |
0.9890 |
1.0032 |
0.9981 |
|
1.9637 |
2.0114 |
1.9922 |
2.0023 |
|
-0.9681 |
-1.0103 |
-0.9945 |
-1.0020 |
|
0.9739 |
1.0214 |
0.994 |
1.0036 |
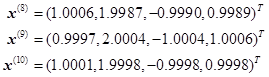
且有误差
![]()
从此例看出,由迭代法产生的向量序列![]() 逐次逼近方程组的精确解。但是,并不是对任何一个方程组(6.8.1)由迭代法产生的向量序列
逐次逼近方程组的精确解。但是,并不是对任何一个方程组(6.8.1)由迭代法产生的向量序列![]() 都收敛。
都收敛。
设有方程组
![]() (6.8.3)
(6.8.3)
其中,![]() 为非奇异矩阵,且
为非奇异矩阵,且![]()
将![]() 写为:
写为:
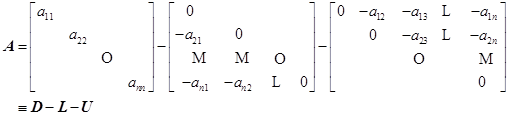 (6.8.4)
(6.8.4)
现将![]() 分裂为
分裂为
![]()
于是方程组(6.8.3)等价与方程组
![]() (6.8.5)
(6.8.5)
其中,![]() 为可选择的一个非奇异矩阵,应选择
为可选择的一个非奇异矩阵,应选择![]() 使
使![]() 容易求解,一般选择为
容易求解,一般选择为![]() 的某种近似。
的某种近似。
对应于方程(6.8.5)可构造一个迭代过程:
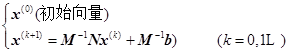 (6.8.6)
(6.8.6)
6.8.1 雅可比(Jacobi)迭代法
选取![]() ,于是
,于是
![]()
方程(6.8.3)的转化为等价方程组
![]()
于是得到雅可比(Jacobi)迭代公式:
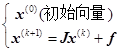 (6.8.7)
(6.8.7)
其中,![]() 。
。![]() 称为Jacobi迭代法的迭代矩阵。
称为Jacobi迭代法的迭代矩阵。
Jacobi迭代公式的分量形式:
引进记![]() 号为第
号为第![]() 次近似,由(6.8.7)式可写为
次近似,由(6.8.7)式可写为
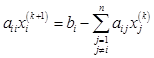
或
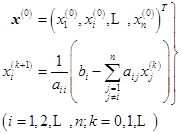 (6.8.8)
(6.8.8)
Jacobi迭代法公式简单,由公式(6.8.7)或(6.8.8)可知,每迭代一次只需计算一次矩阵与向量的乘法,例10的迭代法就是解![]() 的Jacobi迭代法。电算时Jacobi方法需要两组工作单元用来保存
的Jacobi迭代法。电算时Jacobi方法需要两组工作单元用来保存![]() 及
及![]() 且可用
且可用![]() 来控制迭代终止。由迭代法计算公式可知,此迭代法的一个重要特点是计算过程中原来矩阵
来控制迭代终止。由迭代法计算公式可知,此迭代法的一个重要特点是计算过程中原来矩阵![]() 数据始终不变。
数据始终不变。
6.8.2 高斯—塞德尔迭代法
在(6.8.5)式中选取![]() (下三角矩阵),于是
(下三角矩阵),于是![]()
方程(6.8.3)转化为等价方程组
![]()
于是得到高斯—塞德尔(G—S)迭代公式
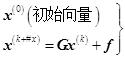 (6.8.9)
(6.8.9)
其中,![]() 。
。![]() 称为
称为![]() 迭代法的迭代矩阵。
迭代法的迭代矩阵。
![]() 迭代法的分量形式:
迭代法的分量形式:
记![]() ,公式(6.8.9)可写成
,公式(6.8.9)可写成
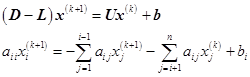
或
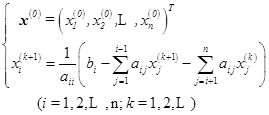 (6.8.10)
(6.8.10)
![]() 迭代法每迭代一次只需要计算一次矩阵与向量的乘法。但
迭代法每迭代一次只需要计算一次矩阵与向量的乘法。但![]() 迭代法比Jacobi迭代法有一个明显的优点,就是电算时仅需用一维数组
迭代法比Jacobi迭代法有一个明显的优点,就是电算时仅需用一维数组![]() 存放
存放![]() 分量(或
分量(或![]() 分量)。当计算出
分量)。当计算出![]() 就冲掉旧分量
就冲掉旧分量![]() 。从
。从![]() 迭代公式(6.8.10)可看出在
迭代公式(6.8.10)可看出在![]() →
→![]() 的一步迭代中,计算分量
的一步迭代中,计算分量![]() 时利用了已经计算出的最新分量
时利用了已经计算出的最新分量![]()
![]() 。因此
。因此![]() 迭代法可看作是Jacobi迭代法的一种修正。
迭代法可看作是Jacobi迭代法的一种修正。
![]() 迭代法计算:
迭代法计算:
(1)![]()
(2)对于![]() ;
;
![]()
例11用![]() 迭代法解例10方程组。
迭代法解例10方程组。
解 ![]() 迭代方法(结果如表6—3)
迭代方法(结果如表6—3)
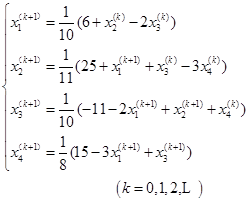
表 6-3
|
|
|
|
|
|
|
|
0.0 |
0.6000 |
1.030 |
1.0065 |
1.0009 |
1.0001 |
|
0.0 |
2.3272 |
2.037 |
2.0036 |
2.0003 |
2.0000 |
|
0.0 |
-0.9873 |
-1.014 |
-1.00025 |
-1.0003 |
-1.0000 |
|
0.0 |
0.8789 |
0.9844 |
0.9983 |
0.9999 |
1.0000 |
且 ![]()
从此例看出,![]() 迭代法比Jacobi迭代法收敛快(初始向量相同,达到同样精度,所需要迭代次数较少)。但这个结论对
迭代法比Jacobi迭代法收敛快(初始向量相同,达到同样精度,所需要迭代次数较少)。但这个结论对![]() 的矩阵
的矩阵![]() 满足某些条件时才是对的,甚至有这样的方程组,用Jacobi方法是收敛的,而用
满足某些条件时才是对的,甚至有这样的方程组,用Jacobi方法是收敛的,而用![]() 迭代法却是发散的。
迭代法却是发散的。
6.8.3解线性方程组的超松弛迭代法
逐次超松弛迭代(Successive Over—Relaxation),简称![]() 方法是
方法是![]() 迭代法的一种加速的方法,是解大型稀疏矩阵方程组的有效方法之一,它有着广泛的应用。
迭代法的一种加速的方法,是解大型稀疏矩阵方程组的有效方法之一,它有着广泛的应用。
设有方程组
![]()
且![]() ,
,![]() 为非奇异矩阵。分解
为非奇异矩阵。分解![]() 为
为![]() 。
。
设已知第![]() 次近似
次近似![]() 及第
及第![]() 次近似的分量
次近似的分量![]() ,首先用
,首先用![]() 迭代法计算一个辅助量
迭代法计算一个辅助量![]() :
:
![]() (6.8.11)
(6.8.11)
再由![]() 的第
的第![]() 个分量
个分量![]() 与
与![]() 加权平均,定义
加权平均,定义![]() :
:
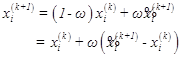 (6.8.12)
(6.8.12)
将(6.8.11)式代入(6.8.12)式,得到解![]() 的
的![]() 方法:
方法:
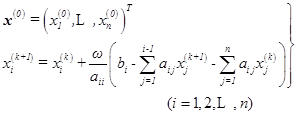 (6.8.13)
(6.8.13)
其中,![]() ,
,![]() 称为松弛因子。
称为松弛因子。
或写为
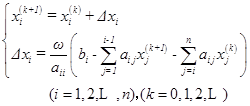
![]()
![]()
在![]() 方法(6.8.13)式中取
方法(6.8.13)式中取![]() ,则
,则![]() 方法就是
方法就是![]() 迭代法,当松弛因子
迭代法,当松弛因子![]() 满足
满足![]() 时,迭代法(6.8.13)式称为低松弛方法。当
时,迭代法(6.8.13)式称为低松弛方法。当![]() 时,迭代法(6.8.13)式称为超松弛方法。
时,迭代法(6.8.13)式称为超松弛方法。
![]() 方法每迭代一次主要计算量是计算一次矩阵乘向量。计算时可用
方法每迭代一次主要计算量是计算一次矩阵乘向量。计算时可用![]() 来控制迭代,且这时
来控制迭代,且这时![]() 方法只需一组工作单元
方法只需一组工作单元![]() 存放
存放![]() 或
或![]() 。也可用剩余向量
。也可用剩余向量![]() 来控制迭代终止。
来控制迭代终止。
例12 用![]() 方法解方程组
方法解方程组
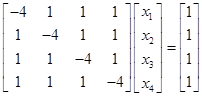
解 精确解![]()
取初始向量![]() ,
,![]() 迭代公式:
迭代公式:
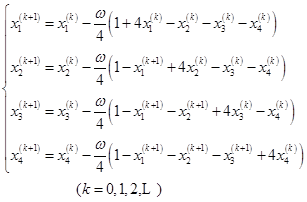
(1)取松弛因子![]() 计算结果为:
计算结果为:
![]()
且
![]()
(2)当取![]() 时,初始向量相同,达到同样的精度,所需要迭代次数
时,初始向量相同,达到同样的精度,所需要迭代次数![]() 。
。
(3)当取![]() 时,初始向量相同,达到同样的精度,所需要迭代次数
时,初始向量相同,达到同样的精度,所需要迭代次数![]() 。
。
对于此例,最佳松弛因子是![]() ,即达到同样精度
,即达到同样精度![]() ,所需要迭代次数最少。由此可知,利用
,所需要迭代次数最少。由此可知,利用![]() 方法解线性方程时,松弛因子选择得较好,常常会使
方法解线性方程时,松弛因子选择得较好,常常会使![]() 迭代收敛大大加速。我们指出,解
迭代收敛大大加速。我们指出,解![]() ,
,![]() 方法收敛的必要条件是:
方法收敛的必要条件是:![]() 。因此,用
。因此,用![]() 方法解
方法解![]() 时松弛因子
时松弛因子![]() 应在
应在![]() 内选择(这时
内选择(这时![]() 方法可能收敛)。
方法可能收敛)。
解![]() 的
的![]() 方法的矩阵形式:
方法的矩阵形式:
由![]() 迭代公式(6.8.13),即
迭代公式(6.8.13),即
![]()
即
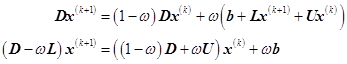
由设![]() ,于是
,于是![]() 为非奇异阵。
为非奇异阵。
解![]() 的
的![]() 方法(设
方法(设![]() 为非奇异且
为非奇异且![]() )的迭代公式的矩阵形式:
)的迭代公式的矩阵形式:
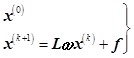 (6.8.14)
(6.8.14)
其中,![]() 。
。![]() 称为
称为![]() 方法的迭代矩阵。
方法的迭代矩阵。
用![]() 方法解
方法解![]() 的框图见图6—3。
的框图见图6—3。
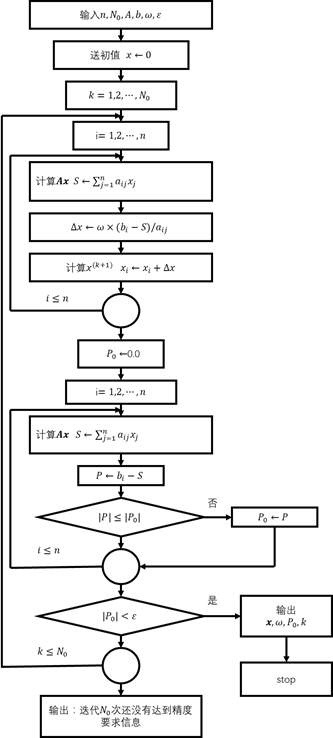
图 6-3
设有方程组![]() ,其中
,其中![]() 满足条件:
满足条件:
(1)![]() 为对称正定阵,或(2)
为对称正定阵,或(2)![]() 为严格对角占优阵(即
为严格对角占优阵(即![]() )等。数组
)等。数组![]() 存放近似解,
存放近似解,![]() 表示迭代的最大次数。当
表示迭代的最大次数。当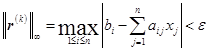 时迭代终止。
时迭代终止。
6.8.4 迭代法的收敛性
由上面讨论可知,解![]() 的Jacobi迭代法﹑
的Jacobi迭代法﹑![]() 迭代法以及
迭代法以及![]() 方法,都是一阶定常迭代法。下面讨论一阶定常迭代法的收敛条件。
方法,都是一阶定常迭代法。下面讨论一阶定常迭代法的收敛条件。
设有方程组
![]() (6.8.15)
(6.8.15)
及迭代法
![]() (6.8.16)
(6.8.16)
需要研究![]() 收敛性,引进误差向量
收敛性,引进误差向量
![]()
由(6.8.16)式减去(6.8.15)式得到误差向量的递推公式
![]() (6.8.17)
(6.8.17)
于是有
![]() (6.8.18)
(6.8.18)
上式表明,要考查![]() 收敛性,就是要研究迭代矩阵
收敛性,就是要研究迭代矩阵![]() 在什么条件下有
在什么条件下有![]() (当
(当![]() ),即需要研究
),即需要研究![]() 满足什么条件有
满足什么条件有![]() (零矩阵)(
(零矩阵)(![]() )(即元素
)(即元素![]() ,当
,当![]() 时)。
时)。
由(6.8.18)式,显然有
![]() (6.8.19)
(6.8.19)
于是,如果给出的迭代法其迭代矩阵![]() 满足
满足![]() ,则
,则![]() (当
(当![]() ),即迭代法(6.8.16)收敛。
),即迭代法(6.8.16)收敛。
定理10 (迭代法收敛的充分条件)
设有方程组![]() ,且
,且![]() 为由迭代法
为由迭代法![]() (
(![]() 为任意选取初始向量)产生的向量序列。
为任意选取初始向量)产生的向量序列。
如果迭代矩阵![]() 有某一种算子范数
有某一种算子范数![]() ,则
,则
(1)![]() 收敛于方程组
收敛于方程组![]() 惟一解
惟一解![]() ;
;
(2)![]() ;
;
(3)有误差估计![]() 。
。
证明 由定理9可知方程组![]() 有唯一解
有唯一解![]() ,即
,即![]() 满足方程组
满足方程组
![]()
由设及式(6.8.19)即得到(1)。
证(2),显然,由迭代公式及(6.8.17)式有
①![]()
②![]()
则
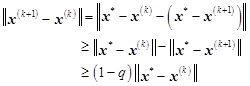
即
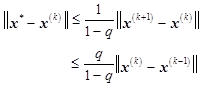
反复利用①情况,即得(3)。
例13 考查用Jacobi方法解例10中方程组的收敛性。
解
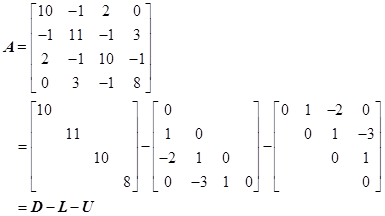
Jacobi迭代阵为:
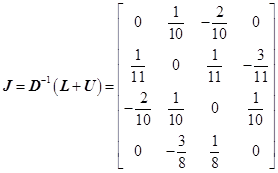
计算 ![]() ,故解此方程组的jacobi方法收敛。
,故解此方程组的jacobi方法收敛。
定义6 设![]() 的特征值为
的特征值为![]() ,
,![]() ,…,
,…,![]() ,称值
,称值
![]() (
(![]() 特征值按模的最大值)
特征值按模的最大值)
为矩阵![]() 的谱半径。
的谱半径。
例14 设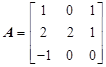 ,计算
,计算![]() 的谱半径。
的谱半径。
解 计算![]() 的特征值,即求特征方程
的特征值,即求特征方程
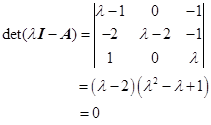
的根。
于是![]() 的特征值为
的特征值为
![]()
![]() 的谱半径为
的谱半径为
![]()
定理11 设![]() ,则
,则![]() (零矩阵)(当
(零矩阵)(当![]() )
)![]() 所有特征值满足
所有特征值满足
![]() 或
或![]() 的谱半径
的谱半径![]()
![]()
定理12 (迭代法基本定理)
(1)设有方程组 ![]()
(2)设有一阶定常迭代法 ![]()
对任意选取初始向量![]() ,迭代法(2)收敛的
,迭代法(2)收敛的![]() 的特征值满足
的特征值满足![]()
![]() 或
或![]()
推论:
(1)雅可比迭代法收敛的充要条件是![]() 。
。
(2)高斯—赛德尔迭代收敛的充要条件是![]() 。
。
(3)超松弛迭代法收敛的充要条件是![]() 。
。
定理12是一阶定常迭代法的收敛准则,在理论上是重要的,当![]() 较大时,一般计算
较大时,一般计算![]() 是困难的。
是困难的。
例15 设
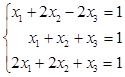
考查用雅可比迭代法和![]() 迭代法解此方程组的收敛性。
迭代法解此方程组的收敛性。
解
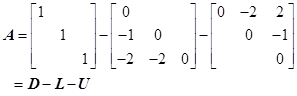
雅可比迭代法的迭代矩阵为
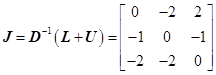
计算![]() 的特征值
的特征值
![]()
得到 ![]()
因此,用雅可比迭代法解此方程组收敛。
![]() 方法的迭代矩阵为
方法的迭代矩阵为
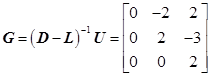
计算![]() 的特征值
的特征值
![]()
得到![]()
所以用![]() 迭代法解此方程组不收敛。
迭代法解此方程组不收敛。
定义7 (严格对角占优阵)设![]()
如果![]() 满足条件
满足条件
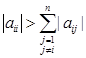
![]()
即![]() 的每一行对角元素的绝对值都严格大于同行其他元素绝对值之和,称
的每一行对角元素的绝对值都严格大于同行其他元素绝对值之和,称![]() 为严格对角占优阵。
为严格对角占优阵。
定理13 如果![]() 为严格对角占优阵,则
为严格对角占优阵,则![]() 为非奇异矩阵。
为非奇异矩阵。
证明 用反正法。若![]() ,则
,则![]() 有非零解,记为
有非零解,记为![]() 。且记
。且记![]() ,于是由
,于是由![]() 的第
的第![]() 个方程
个方程
![]()
得到
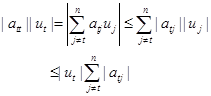
即
![]()
与假设矛盾。
定理14 设![]() ,
,![]() 。
。
如果![]() 为严格对角占优阵,则解
为严格对角占优阵,则解![]() 的Jacobi方法,
的Jacobi方法,![]() 迭代法都收敛。
迭代法都收敛。
证明 (1)首先证明解![]() 的Jacobi方法收敛。由假设有
的Jacobi方法收敛。由假设有
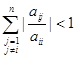
![]()
解![]() 的Jacobi方法迭代矩阵为
的Jacobi方法迭代矩阵为![]() ,且由式(6.8.20)有
,且由式(6.8.20)有
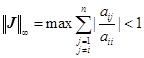
故由定理10知解![]() 的Jacobi方法收敛。
的Jacobi方法收敛。
(2)记![]()
由假设有
![]()
![]()
即有 ![]() 或
或 ![]()
(6.8.21)
由![]() 迭代法的迭代矩阵为
迭代法的迭代矩阵为![]() ,假设
,假设![]() 为严格对角占优阵,下面来说明
为严格对角占优阵,下面来说明
![]()
记 ![]()
即 ![]()
或
![]() (6.8.22)
(6.8.22)
记 ![]()
取(6.8.22)式第![]() 个分量得到
个分量得到
![]()
![]()
于是
![]() (6.8.23)
(6.8.23)
由(6.8.23)式整理即得到
![]()
(对任何![]() )
)
则有
![]()
故定理10知解![]() 的
的![]() 迭代法收敛。
迭代法收敛。
定理15 (1)设![]() ,其中
,其中![]() 为对称正定阵;
为对称正定阵;
(2)![]() ;
;
且 解![]() 的
的![]() 方法收敛。
方法收敛。
例16 设有方程组如下,试考查用Jacobi方法,![]() 迭代法解此方程组的收敛性:
迭代法解此方程组的收敛性:
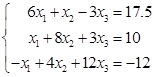
解 由于
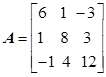
为严格对角占优阵,于是由定理14可知解![]() 的Jacobi迭代,
的Jacobi迭代,![]() 迭代均收敛。
迭代均收敛。
