当前位置:课程学习>>第七章>>知识讲解>>视频课堂>>知识点二
知识点二:欧拉方法
内容导入
欧拉方法的出发点为离散化和取泰勒展开式近似值。
教师解析
内容简介
对于初值问题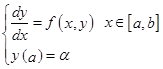 ,先将其离散化,即把
,先将其离散化,即把![]() 作
作![]() 等分,得各离散节点
等分,得各离散节点![]()
![]() ,式中,
,式中,![]() 。
。
设![]() 为方程的解,则
为方程的解,则![]() 在点
在点![]() 处的泰勒展开式为
处的泰勒展开式为 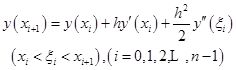 。当
。当![]() 有界且
有界且![]() 充分小时,可忽略高阶无穷小量
充分小时,可忽略高阶无穷小量![]() ,将上式写成
,将上式写成
![]() 或
或![]() 。
。
若将![]() 和
和![]() 的近似值分别记为
的近似值分别记为![]() ,这就是欧拉(Euler)公式,又称欧拉一步格式。
,这就是欧拉(Euler)公式,又称欧拉一步格式。
用向后差商表示的两点数值微分公式得到后欧拉格式。用中心差商表示的三点数值微分公式得到两步欧拉格式。预测—校正方法称为改进的欧拉格式。
边学边练
练习题1 用欧拉格式计算初值问题
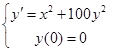 的解函数
的解函数![]() 在
在![]() 时的近似值(取步长
时的近似值(取步长![]() 保留到小数点后4位)。
保留到小数点后4位)。
练习题2 用改进的Euler格式计算积分![]() 在
在![]() 时的近似值(保留到小数点后6位)。
时的近似值(保留到小数点后6位)。
 视频学习资源下载
视频学习资源下载
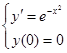 ,并且取步长
,并且取步长