7.1 常微分方程的数值解法引言

在工程和科学技术的实际问题中，常需求解常微分方程。但常微分方程中往往只有少数较简单和典型的常微分方程（例如线性常系数常微分方程等）可求出其解析解。对于变系数常微分方程的解析求解就比较困难，而一般的非线性常微分方程就更不用说了。在大多数情况下，常微分方程只能用近似法求解。这种近似解法可分为两大类：一类是近似解析法，如级数解法、逐次逼近法等；另一类则是数值解法，它给出方程在一些离散点上的近似解。

在具体求解微分方程时，需要具备某种定解条件，微分方程和定解条件合在一起组成定解问题。定解条件有两种：一种是给出积分曲线在初始点的状态，称为初始条件，相应的定解问题称为初值问题；另一种是给出积分曲线首尾两端的状态，称为边界条件，相应的定解问题则称为边值问题。

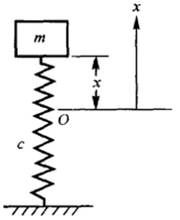
图 7-1

例如，弹簧—质量系统的振动问题（图 7-1），作一定的简化后，可用一个二阶常微分方程

来描述。式中，是质量离平衡位置（点）的距离；是时间；是弹簧常数。

当弹簧的振动开始时刻时的初始位置和初始速度都确定时，弹簧的振动规律也就惟一确定。这就是一个常微分方程的初值问题，可写成

本章介绍常微分方程的数值解法。先从最简单的一阶常微分方程的初值问题

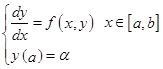　　　　　　　　　　　　　　　　（7.1.1）

出发进行讨论。

由常微分方程的理论可知，只要上式中的函数在区域内连续，且关于满足李普希兹（Lipschitz）条件，即存在常数(它与无关)使

对内任意两个和都成立，则方程（7.1.1）的解必定存在且惟一。下面的分析均假定满足上述条件。

至于初值问题（7.1.1）式的数值解法，常采用差分方法，即把一个连续的初值问题离散化为一个差分方程来求解。具体地说，就是将方程（7.1.1）离散化后，求找其解在一系列离散节点

上的近似值。

两相邻节点间距离

  

称为步长。当 (常值)时称为等步长，有

   

或

  

因为初值问题中的初始条件为已知，即可利用已知的来求出下一个节点处的近似值，再从来求出……如此继续，直到求出为止。这种用按节点的排序顺序一步一步地向前推进的方式求解的差分算法称为步进式或递推式算法。它是初值问题数值解法的各种差分格式的共同特点。因此，只要能写出前几步已知信息来计算的递推公式（即差分格式），即可完全表达该种算法。