7.2 欧拉方法

7.2.1 欧拉格式

对于初值问题（7.1.1）式，先将其离散化，即把作等分，得各离散节点

 

式中，。

设为方程的解，则在点处的泰勒展开式为

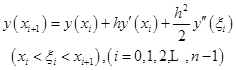             （7.2.1）

当有界且充分小时，可忽略高阶无穷小量，将上式写成

或　　　

若将和的近似值分别记为

          　　（7.2.2）

这就是欧拉（Euler）公式，又称欧拉格式。利用它可由已知的初值出发，逐步算出。这类形式的方程也称为差分方程。

当假定为准确的，即在的前提下来估计误差，这种截断误差称为局部截断误差。由式（7.2.1）和（7.2.2）可知，欧拉格式在节点处的局部截断误差显然为

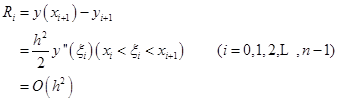
如果局部截断误差为,则称这种数值算法的精度为阶。故欧拉格式的精度为一阶。

从图7—2可看出欧拉格式的几何意义。由方程（7.1.1）知，其积分曲线上任意一点的切线斜率都等于函数的值。从初始点（即点）出发，作积分在点上的切线（其斜率为）,与直线相交与点（即点）,得到作为的近似值，则有

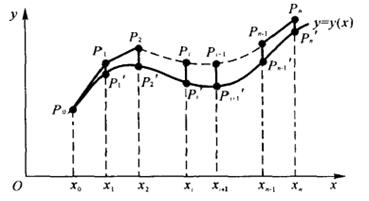
图 7-2

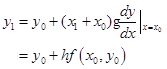
与   　

相比较可知，这时是用切线近似代替了曲线；点近似代替了点；近似代替了；近似代替了。

递推：继续从点出发，作一斜率为的直线，与直线相交于点点（即点），得到作为的近似值…如此继续，知道点。这样，得出一条折线近似代替积分曲线。当步数越多时，由于误差的积累，折线可能会越来越偏离真解曲线。

因为差分是微分的近似运算，所以欧拉格式也可用差商近似代替导数的离散方法来得到。在节点处，有

       　　　　　　　　（7.2.4）

用向前差商近似代替上式中的导数项,即式

　  　　　　  　　　　　（7.2.5）

代入式（7.2.4），可得

和分别用其近似值和代入，则得

此即为式（7.2.2）（欧拉格式）。

显然，欧拉格式具有递推性，在计算时只要用到前一步所得结果一个信息就够了，因此是一种单步格式，或称一步格式。

其中，式（7.2.5）是一个数值微分公式。故用其他数值微分公式也可导出略异于式（7.2.2）的其他形式的算式来。例如，用向后差商表示的两点数值微分公式

  

代入

  

可得　　

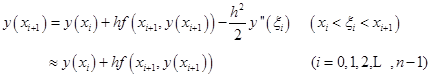
和分别用其近似值和代入，则得

　　　　　　　　　　　（7.2.6）

其局部截断误差显然为

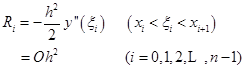      　　　　　　　　（7.2.7）

式（7.2.6）称为向后欧拉格式，又称为隐式欧拉格式。因为在此式的右边也包含未知的,所以式（7.2.6）是的一个函数方程，故称它为隐式格式。式(7.2.2)的右边则没有未知的，因此是一种显式格式。隐式格式的计算当然比显式格式要困难得多，一般情况下，只能用迭代法求解，计算工作量较大。

再如，用中心差商表示的三点数值微分公式

　　　　　　

代入

可得

　　　　　

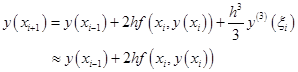
, 和分别用近似值, 和代入，则得

  　　　　　　（7.2.8）

显然，其局部截断误差为

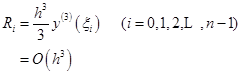　　　　　　　　　（7.2.9）

不论是显式欧拉格式（7.2.2），还是隐式欧拉格式（7.2.6），它们都是单步格式，或称一步格式。因为它们在计算时，只用到前一步所得结果一个信息就够了；而格式（7.2.8）则除了外，还需用到更前一步所得信息，即需调用前两步的信息，因此式（7.2.8）称为两步欧拉格式，或称中点欧拉格式（因为用到中心差商）。

比较式（7.2.3），（7.2.7）和（7.2.9）可知，两步欧拉格式比显式或隐式欧拉格式具有更高的精度，因为它的局部截断误差是。

由式（7.2.3）和（7.2.7）可见，显式欧拉格式与隐式欧拉格式的局部截断误差的符号正好相反，因此可以设想取式（7.2.2）和（7.2.6）的平均，即两式相加除以2，可得

 　　　　　

将会使误差相互抵消，提高误差阶数，从而提高算法的精度。事实上，格式（7.3.10）的局部截断误差为，即其精度为二阶。式（7.2.10）成为梯形格式，是一种隐式格式。

从几何角度上来看，梯形格式是取的两端点的平均斜率。由图7—3可见，用梯形格式得到的点，显然比用显式欧拉格式得到的点和隐式欧拉格式得到的B点都要合理。

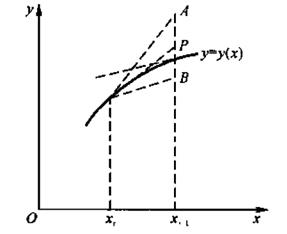
图 7-3

欧拉格式（7.2.2）的程序框图见图7-4。

图7-4

7.2.2 改进的欧拉格式

显示欧拉格式计算工作量小，但精度低。梯形格式虽提高了精度，但为隐式格式，需用迭代法求解，计算工作量大。综合这两种格式可得到改进的欧拉格式。

    选用欧拉格式（7.2.2）求出一个初步的近似值,称为预测值，它的精度不高，接着用梯形格式（7.2.10）对它校正一次，即迭代一次，求得,称为校正值。这种预测—校正方法称为改进的欧拉格式：

 　　　　　

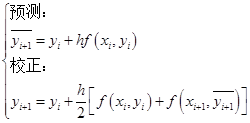
可以证明，（7.2.11）格式的精度为二阶。它是一种一步显示格式。式（7.2.11）也可以写成

　（7.2.12）

或将它写成下列平均化的形式

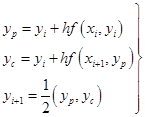
   　　　　　（7.2.13）

改进的欧拉格式（7.2.13）的程序框图见图7-5。

 

图 7-5

 

例1 试分别用欧拉格式和改进的欧拉格式求解下列初值问题，并比较两法所得计算结果的精度：

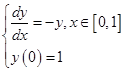
解 取步长。这样，欧拉格式和改进的欧拉格式的具体算式分别为

及　　

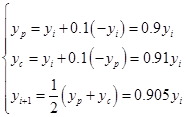
两种格式的计算结果分别列于表7—1中。

表 7-1

	欧拉公式		改进后的欧拉公式		精确解
0	1		1		1
0.1	0.9000000	4.8374	0.9050000	1.626	0.9048374
0.2	0.8100000	8.7308	0.8190250	2.492	0.8187308
0.3	0.7290000	1.18182	0.7412176	3.994	0.7408182
0.4	0.6561000	1.4220	0.6708020	4.820	0.6703200
0.5	0.5904900	1.60407	0.6070758	5.451	0.6065307
0.6	0.5314410	1.73706	0.5494036	5.920	0.5488116
0.7	0.4782969	1.82884	0.4972102	6.249	0.4965853
0.8	0.4304672	1.88618	0.4499753	6.463	0.4493290
0.9	0.3874205	1.91492	0.4072276	6.579	0.4065697
1	0.3486784	1.92010	0.3685410	6.616	0.3678794

由上表可见，与精确解相比，改进的欧拉格式的精度较欧拉格式有明显的提高。