7.3 龙格——库塔方法

如欲再进一步提高求解的精度，可用一种高精度的单步法——龙格——库塔（Runge—Kutta）方法，简称方法。它采用了间接使用泰勒级数法的技术。

7.3.1 龙格—库塔公式的导出

对于一阶常微分方程（7.1.1）的解,可以利用微分中值定理得

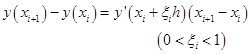
即

也即　　

          　　　  　　　（7.3.1）

式中

　　　　　　　　　　　　　　（7.3.2）

可以看作是在区间上的平均斜率。这样，欧拉公式（7.2.2）相当于取点上的斜率作为平均斜率的近似值，这当然是十分粗糙的，因此精度必然很低。而改进的欧拉格式（7.2.12）可改写成

         

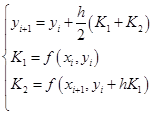
与式（7.3.1)比较可知，它相当于把和两个点上的斜率和的算术平均值作为（7.3.1）式中的平均斜率的近似值。其中是通过已知信息来近似地预测的。

由此可以设想，取区间内的某一个节点

上的斜率与点上的斜率作线性组合（即加权平均），作为平均斜率的近似值，即

为了要得到点上的斜率，需先预测

根据预测值再来算出，即

由此构成的计算格式为

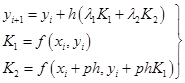
  　　　　　　　　　　（7.3.3）

式（7.3.3）中含有三个待定参数：和,适当选定它们的值可使算法的局部截断误差为,从而具有二阶精度。

假定,分别将和做泰勒展开：

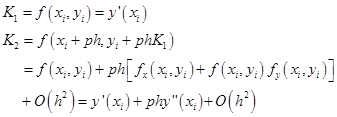
代入式（7.3.3），得

把它与在处的二阶泰勒展开式

进行比较系数后可知，只要

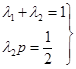　　　　　　　　　　　　　　　　　　　　　　　　　　（7.3.4）

成立，格式（7.3.3）局部截断误差就等于，从而能具有二阶精度。

式（7.3.4）中有三个待定参数，但却只有两个方程式，因此还有一个自由度。凡满足条件（7.3.4）式的一族格式（7.3.3）统称为二阶龙格——库塔（）格式。

当,时，时，二阶格式（7.3.3）即为改进的欧拉格式（7.2.12）。

如取，则及，式（7.3.3）就成为

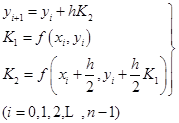　　　　　　　　　　　　　　　　　　　　　　（7.3.5）

称为变形的欧拉格式

由于式（7.3.5）中的是由欧拉格式预测出来的区间的中点的近似解，就近似等于此中点的斜率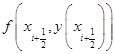，因此式（7.3.5）就相当于用中点的斜率作为式（7.3.1）的平均斜率的近似值，故格式（7.3.5）也称为中点格式。

粗看起来，中只显含一个斜率值，但实际上是通过才算出来的，因此，式中还隐含着。这样，每完成一步仍需计算函数值两次，其计算工作量仍与改进的欧拉格式一样。

3.2 高阶龙格——库塔格式

如欲再提高精度，可在区间内取两个节点

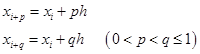
上的斜率和，与点上的斜率加权平均，作为平均斜率的近似值，即

其中，和仍如式（7.3.3）。

利用区间内的两个斜率和，加权平均作为其平均斜率，来预测；

从而得到

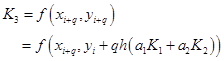
由此构成的计算格式为

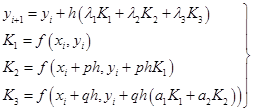　　　　　　　　　　　　　　　　　　（7.3.6）

类似于二阶龙格－库塔格式的导出过程，运用泰勒展开的方法，可找出欲使格式（7.3.6）的局部截断误差为，从而具有三阶精度所必须满足的条件为：

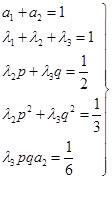　　　　　　　　　　　　　　　　　　　　　　　　　　　（7.3.7）

其中，共有七个待定参数，但只有五个方程式，因此还有两个自由度。凡满足条件（7.3.7）式的一族格式（7.3.6）统称为三阶龙格－库塔格式。

当待定系数取为

时的三阶龙格－库塔格式称为库塔格式，其具体形式为：

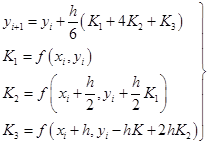　　　　　　　　　　　　　　　　　　　（7.3.8）

继续推广这种处理过程，可得四阶龙格－库塔格式，是最常用的一种经典龙格－库塔格式，其具体形式如下：

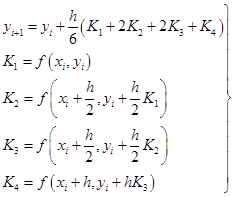　　　　　　　　　　　　　　　　　　（7.3.9）

经典龙格－库塔格式的程序框图见图7-6。

图 7-6

例2 试分别用欧拉方法（）、改进欧拉方法（）及经典方法（）求解下列初值问题，并比较三种方法所得结果的精度

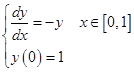
解　三种方法的具体算式分别如下：

欧拉格式

改进的欧拉格式

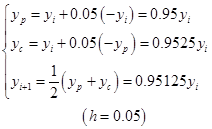
经典格式

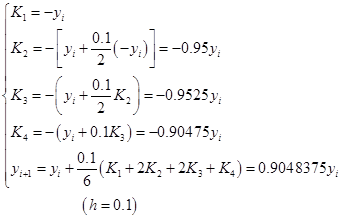
三种格式的计算结果分别列于下表中。

表 7-2

	欧拉方法 （）		该井的欧拉方法 （）		经典P-K方法 （）		精度解
0	1		1		1		1
0.1	0.903687890	0.0011495	0.904876562	0.000039144	0.904837500	0.000000082	0.904837418
0.2	0.816651803	0.0020790	0.818801593	0.000070840	0.818730901	0.000000148	0.818730753
0.3	0.737998345	0.0028200	0.740914371	0.000096151	0.740818422	0.000000202	0.740818220
0.4	0.666920168	0.0034000	0.670436049	0.000116000	0.670320289	0.000000243	0.670320046
0.5	0.602687680	0.0038430	0.606661867	0.00013121	0.606530934	0.000000275	0.606530659
0.6	0.544641558	0.0041701	0.548954105	0.00014247	0.548811934	0.000000298	0.548811636
0.7	0.492185981	0.0043993	0.496735704	0.00015040	0.496585618	0.000000315	0.496585303
0.8	0.444782511	0.0045465	0.449484496	0.00015553	0.449329289	0.000000325	0.449328964
0.9	0.401944569	0.0046251	0.406727985	0.00015833	0.406569991	0.000000332	0.406569659
1	0.363232440	0.0046470	0.368038621	0.00015918	0.367879774	0.000000333	0.367879441

这里对三种方法采用了不同的步长值，是为了使它们所耗的计算工作量大致相同，以便于比较。从表7-2可见，经典方法的精度较改进的欧拉方法又有很大的提高。关于这一结论也可从理论上大致分析出来：

欧拉方法的局部截断误差为,计算四步后

而经典方法的局部截断误差则为

所以为大致相同数量级下的常数，故有

但要注意的是，方法的导出利用了泰勒展开，因此要求所求的解有较好的光滑性，如果解得光滑性，如果解的光滑性差，则采用经典法所得的数值解，其精度有可能反而不及改进的欧拉法。因此，在实际计算中，应根据问题的具体情况来选择合适的算法。

7.3.3   步长的自动选择

在用数值法求解微分方程的过程中，选取适当的步长是至关重要的。如步长太大则达不到精度的要求；步长太小则步数增多，不但会增加计算工作量，而且可能导致舍入误差的严重累积。尤其是当微分方程的解y(x)变化较剧烈时，步长的合理取法是在变化剧烈处步长应取得小些；在变化平缓处步长应取得大些，也就是采用自动选择步长的变步长方法，即根据精度要求，先估计出下一步长的合理大小，然后按此来进行计算。这里介绍一种李查逊（Richardson）外推法。

从节点出发，先以h为步长，跨一步到节点,求出一个近似值.如计算公式是p阶的，则

            （7.3.10）

当h值不大时，式中的系数c可近似地看作为常数。

然后将步长减半，即以为步长，从节点出发，跨两步到节点,再求得一个近似值.其中没跨一步的截断误差为,故有

            （7.3.11）

式（7.3.11）-式（7.3.10）得

即

由上式可见，如取

作为近似值，则显然比和的精度都要高。

当p=4时，可取

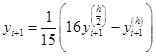
这种修正的方法与龙贝格数值积分法的思路是一致的。

式（7.3.11）除以式（7.3.10）得

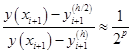
由此可得误差事后估计式

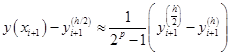
我们就可从选步长减半前后的两次计算结果的偏差

来判别所选步长是否适当。当要求的数值精度为时：

⑴如果则反复加倍步长进行计算，直到时为止，并以上一次步长的计算结果作为；

⑵如果则反复减半步长进行计算，直到为止，并取其最后一次步长的计算结果作为。

这样做时，为了选择步长，每一步都要反复判别，增加了计算工作量，但在方程的解变化剧烈的情况下，总的计算工作量可以得到减少，结果还是合算的。