知识点四:阿达姆斯方法
7.4 阿达姆斯方法
4.1 线性多步方法
前面介绍的几种步进方法在计算![]() 时,大多只用到前一个节点上的近似值
时,大多只用到前一个节点上的近似值![]() ,而没有用到前几步计算所得出的信息,故称单步法。实际上,经过多次单步法计算后,己得出一系列近似值
,而没有用到前几步计算所得出的信息,故称单步法。实际上,经过多次单步法计算后,己得出一系列近似值![]() 和
和![]() 等。为了充分利用这些信息来计算
等。为了充分利用这些信息来计算![]() ,以减少计算工作量和获得较高的精度,可采用如下的计算公式:
,以减少计算工作量和获得较高的精度,可采用如下的计算公式:
![]() (7.4.1)
(7.4.1)
其中,![]() 和
和![]() 为常数,
为常数,![]() 。
。
式(7.4.1)是用前面若干节点处的函数值与导数值的线性组合来计算![]() 的近似值
的近似值![]() ,所以通称为线性多步法。
,所以通称为线性多步法。
当![]() 时为单步法,
时为单步法,![]() 时为多步法(
时为多步法(![]() 步法)。当
步法)。当![]() 时为显式,
时为显式,![]() 时为隐式。前面讲过的中点欧拉格式(7.2.8)就属于多步法(二步法)。
时为隐式。前面讲过的中点欧拉格式(7.2.8)就属于多步法(二步法)。
式(7.4.1)的系数可利用泰勒展开后的待定系数法确定。
4.2 显式和隐式阿达姆斯格式
线性多步法(7.4.1)式中的某些特殊公式,也可由数值积分法来导出。
将微分方程(7.1.1)的两边从![]() 到
到![]() 积分,即可改写成等价的积分方程
积分,即可改写成等价的积分方程
![]() (7.4.2)
(7.4.2)
由于上式中的![]() 内包含了未知函数
内包含了未知函数![]() ,因此等式右边的积分无法直接算出,但可利用数值积分公式导出一系列计算方法。现用牛顿向后插值多项式来逼近式(7.4.2)中的
,因此等式右边的积分无法直接算出,但可利用数值积分公式导出一系列计算方法。现用牛顿向后插值多项式来逼近式(7.4.2)中的![]() ,以导出一种线性多步法——阿达姆斯(Adams)方法。
,以导出一种线性多步法——阿达姆斯(Adams)方法。
设由![]() 共
共![]() 个数据来构造一个
个数据来构造一个![]() 阶牛顿向后插值多项式
阶牛顿向后插值多项式![]() ,则由第二章可知,
,则由第二章可知,![]() 阶牛顿向后插值公式为
阶牛顿向后插值公式为
![]()
其余项为
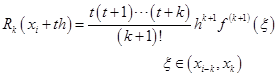
把它们代入式(7.4.2),且利用![]() ,可得
,可得
![]() (7.4.3)
(7.4.3)
当![]() 有界,且
有界,且![]() 时,可以估计出上式中的
时,可以估计出上式中的
![]()
此即为截断误差项。于是可得
![]() (7.4.4)
(7.4.4)
当![]() 时:
时:
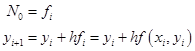
即为显式欧拉格式,其局部截断误差为
![]()
当![]() 时:
时:
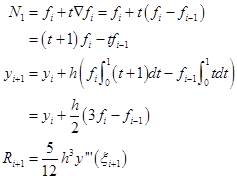
因为 ![]() 及
及![]()
所以
![]() (7.4.5)
(7.4.5)
式中 ![]()
把式(7.4.5)代入式(7.4.4)后,可得
![]() (7.4.6)
(7.4.6)
式中
![]()
所以
![]()
代入式(7.4.6)后得
![]()
其中
![]()
局部截断误差为
![]()
对应于不同![]() 值下的
值下的![]() 和
和![]() 值均可算出,并分别列于下表中。
值均可算出,并分别列于下表中。
表 7-3
 |
0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | 1 | 1/2 | |||||
| 1 | 3/2 | -1/2 | 5/12 | ||||
| 2 | 23/12 | -16/12 | 5/12 | 3/8 | |||
| 3 | 55/24 | -59/24 | 37/24 | -9/24 | 251/720 | ||
| 4 | 1901/720 | -2774/720 | 2626/720 | -1274/720 | 251/720 | 95/288 | |
| 5 | 4277/1440 | -7923/1440 | 9982/1440 | -7298/1440 | 2877/1440 | -476/1440 | 10987/60480 |
当![]() 时,
时,
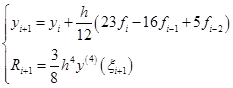
当![]() 时,
时,
 (7.4.7)
(7.4.7)
其中,![]() 时的式(7.4.7)成为阿达姆斯四步显式方法,因为它要用到前面四个节点上的
时的式(7.4.7)成为阿达姆斯四步显式方法,因为它要用到前面四个节点上的![]() 值,是一种最常用的多步算法,其精度为四阶。
值,是一种最常用的多步算法,其精度为四阶。
式(7.4.2)中的![]() 也可用牛顿内插多项式来逼近。设由
也可用牛顿内插多项式来逼近。设由![]() 共
共![]() 个数据来构造一个牛顿内插多项式
个数据来构造一个牛顿内插多项式![]() 则与上面类似推导,可得
则与上面类似推导,可得
![]()
局部截断误差为
![]()
对于不同![]() 值下的
值下的![]() 和
和![]() 值均可算出,并分别列于下表中。
值均可算出,并分别列于下表中。
表 7-4
 |
0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | 1 | -1/2 | |||||
| 1 | 1/2 | 1/2 | -1/12 | ||||
| 2 | 5/12 | 8/12 | -1/12 | -1/24 | |||
| 3 | 9/12 | 19/24 | -5/24 | 1/24 | -19/720 | ||
| 4 | 251/720 | 646/720 | -261/720 | 106/720 | -19/720 | -3/160 | |
| 5 | 475/1440 | 1427/1440 | -798/1440 | 482/1440 | -173/1440 | 27/1440 | -863/60480 |
当![]() 时,
时,
![]()
即为隐式欧拉格式,其局部截断误差为
![]()
当![]() 时,
时,
![]()
即为梯形格式,其局部截断误差为
![]()
当![]() 时,
时,
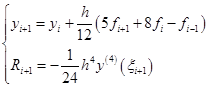
当![]() 时,
时,
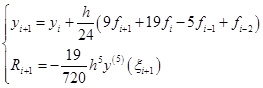 (7.4.8)
(7.4.8)
其中,![]() 时的式(7.4.8)称为三步四阶阿达姆斯隐式算法,它只用到前面三个节点上的
时的式(7.4.8)称为三步四阶阿达姆斯隐式算法,它只用到前面三个节点上的![]() 值,但其精度却是四阶。
值,但其精度却是四阶。
阿达姆斯方法显式与隐式的比较如下:
⑴同一阶数下,隐式的局部截断误差的系数的绝对值![]() 比显式的
比显式的![]() 要小;
要小;
⑵显式的计算工作量比隐式的小;
⑶隐式的稳定范围比显式的大。
例3 试分别用阿达姆斯四步显式方法和三步隐式方法求解下列初值问题,并比较两者所得结果的精度:
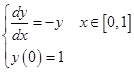
解 取![]()
两种方法的具体算式如下:
四步显式方法
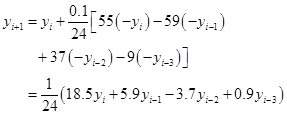 (7.4.9)
(7.4.9)
三步隐式方法
![]()
即
![]() (7.4.10)
(7.4.10)
预测点(初值)可用同阶的![]() 法计算。本例题中则是从精确解(已知
法计算。本例题中则是从精确解(已知![]() )算出。
)算出。
由式(7.4.9)及(7.4.10)算出的结果分别列于下表中。
表 7-5
| 四步显式方法 | 三步隐式方法 | 精度解 |
|||
| 0.3 | 0.740818006 | 2.14×10-7 | 0.740818220 | ||
| 0.4 | 0.670322919 | 2.873×10-6 | 0.670319661 | 3.85×10-7 | 0.670320046 |
| 0.5 | 0.606535474 | 4.815×10-6 | 0.606530138 | 5.12×10-7 | 0.606530659 |
| 0.6 | 0.548818406 | 6.770×10-6 | 0.548811007 | 6.29×10-7 | 0.548811636 |
| 0.7 | 0.496593391 | 8.088×10-6 | 0.496584592 | 7.11×10-7 | 0.496585303 |
| 0.8 | 0.449228154 | 9.190×10-6 | 0.449328191 | 7.73×10-7 | 0.449328964 |
| 0.9 | 0.406579611 | 9.952×10-6 | 0.406568844 | 8.15×10-7 | 0.406569659 |
| 1 | 0.367889955 | 1.051×10-6 | 0.367878598 | 8.43×10-7 | 0.3678794 |
从表种可见,隐式的精度比同阶显式的要高。
4.3 阿达姆斯预测——校正方法
阿达姆斯隐式方法在计算过程中,一般往往遇到要解超越方程。例如下列定解问题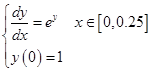
其阿达姆斯三步隐式方法的算式为
![]()
很难化成![]() 的显式表达,只能用迭代的方法,这就会增加计算工作量。因此,在实际计算中,往往仿照改进的欧拉格式的构造方法,把显式和隐式两种阿达姆斯格式结合起来,构成预测-校正系统。
的显式表达,只能用迭代的方法,这就会增加计算工作量。因此,在实际计算中,往往仿照改进的欧拉格式的构造方法,把显式和隐式两种阿达姆斯格式结合起来,构成预测-校正系统。
以四阶阿达姆斯方法为例,先由显式方法算出近似值,作为隐式方法的预测值,然后再做校正。
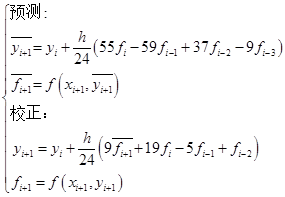 (7.4.11)
(7.4.11)
用上式计算![]() 时,既要用到它前一步的信息
时,既要用到它前一步的信息![]() 和
和![]() ,还要用到更前面三步的信息
,还要用到更前面三步的信息![]() ,
,![]() 和
和![]() 。它是一种四步法,无法自行启动,需用其他四阶单步法(如四阶
。它是一种四步法,无法自行启动,需用其他四阶单步法(如四阶![]() 方法)先从
方法)先从![]() 算出
算出![]() ,
,![]() 和
和![]() 作为其初值,然后按式(7.4.11)进行迭代。
作为其初值,然后按式(7.4.11)进行迭代。
阿达姆斯预测—校正方法的程序框图见图7-7。
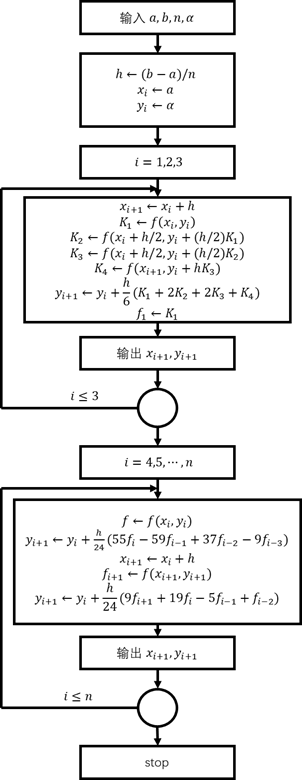
图 7-7
例4 试用阿达姆斯预测—校正方法求解下列初值问题:
解 取![]() 。按式(7.4.11)进行计算,计算结果列于下表中。
。按式(7.4.11)进行计算,计算结果列于下表中。
|
|
|
|
0 0.1 0.2 0.3 |
|
1 1.0954 1.1832 1.2649 |
1 1.0954 1.1832 1.2649 |
0.4 0.5 0.6 0.7 0.8 0.9 1 |
1.3405 1.4141 1.4832 1.5491 1.6124 1.6733 1.7320 |
1.3416 1.4142 1.4832 1.5492 1.6124 1.6733 1.7320 |
1.3416 1.4142 1.4832 1.5492 1.6125 1.6733 1.7321 |
表中的![]() ,
,![]() 和
和![]() 分别为预测值,校正值和精确解(
分别为预测值,校正值和精确解(![]() )。
)。
4.4 阿达姆斯预测——矫正方法的改进
阿达姆斯预测——校正方法与李查逊外推法相结合,可以提高计算精度而不会增加过大的计算工作量。
预测公式的局部截断误差为
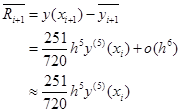 (7.4.12)
(7.4.12)
校正公式的局部截断误差为
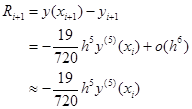 (7.4.13)
(7.4.13)
式(7.4.12)—式(7.4.13)得
![]()
即
![]()
把上式分别代入式(7.4.12)和(7.4.13),可得
![]()
即
![]()
由上两式可知,如果采用式中方括号内的![]() 与
与![]() 的组合,可望使局部截断误差达到O(
的组合,可望使局部截断误差达到O(![]() ),即精度可望提高一阶。
),即精度可望提高一阶。
设![]() 和
和![]() 分别为第i步的预测值和校正值,则可取
分别为第i步的预测值和校正值,则可取
![]()
和
![]()
分别作为![]() 的改进值,其具体算式如下:
的改进值,其具体算式如下:
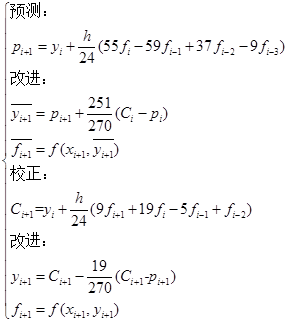 (7.4.14)
(7.4.14)
用(7.4.14)式计算![]() 时需要用到前几步的信息
时需要用到前几步的信息![]() 和
和![]() ,故无法自行启动,也需要用其他四阶单步法(如四阶R-K方法)算出
,故无法自行启动,也需要用其他四阶单步法(如四阶R-K方法)算出![]() 作为其初值,然后按式(7.4.14)进行迭代计算。其中,
作为其初值,然后按式(7.4.14)进行迭代计算。其中,![]() 可令其为零。
可令其为零。
