1:用Euler法、隐式Euler法、梯形法及改进Euler法求解![]() ,取
,取![]() ,计算到
,计算到![]() ,并与精确解比较.
,并与精确解比较.
2:用改进的欧拉法(预报-校正公式)求解初值问题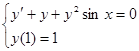 ,取步长h=0.2,计算 y(1.2),y(1.4)的近似值,小数点后至少保留5位。
,取步长h=0.2,计算 y(1.2),y(1.4)的近似值,小数点后至少保留5位。
3:写出用四阶龙格-库塔法求解初值问题![]() 的计算公式,取步长h=0.2计算y(0.4)的近似值。至少保留四位小数。
的计算公式,取步长h=0.2计算y(0.4)的近似值。至少保留四位小数。
1:用Euler法、隐式Euler法、梯形法及改进Euler法求解![]() ,取
,取![]() ,计算到
,计算到![]() ,并与精确解比较.
,并与精确解比较.
解:由于![]() ,
,![]()
![]() ,
,![]()
Euler法:
![]()
![]()
![]() 时,
时,![]() .
.
隐式Euler法:![]()
解出![]()
当![]() 时,
时,![]()
梯形法:![]()
![]()
解出![]()
![]()
当![]() 时,
时,![]()
改进Euler法:
![]()
即 ![]()
![]()
![]()
当![]() 时,
时, ![]()
精确解:![]() ,(梯形法效果最好,改进Euler较好:具有相同的误差数量级,其它不好!)
,(梯形法效果最好,改进Euler较好:具有相同的误差数量级,其它不好!)
| Euler法 |
隐式Euler法 |
梯形法 |
改进Euler法 |
精确解 |
|
| 0.1 | 1.000 000 | 1.009 091 | 1.004 762 | 1.005 000 | 1.004 837 |
| 0.2 | 1.010 000 | 1.026 446 | 1.018 594 | 1.019 025 | 1.019 731 |
| 0.3 | 1.029 000 | 1.051 315 | 1.040 633 | 1.041 218 | 1.040 818 |
| 0.4 | 1.056 100 | 1.083 014 | 1.070 097 | 1.070 802 | 1.070 320 |
| 0.5 | 1.090 490 | 1.120 922 | 1.106 278 | 1.107 076 | 1.106 531 |
2: 用改进的欧拉法(预报-校正公式)求解初值问题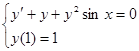 ,取步长h=0.2,计算 y(1.2),y(1.4)的近似值,小数点后至少保留5位。
,取步长h=0.2,计算 y(1.2),y(1.4)的近似值,小数点后至少保留5位。
解 步长h=0.2, 此时f(x,y)=-y-y2sinx
欧拉预报-校正公式为: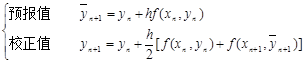
有迭代公式: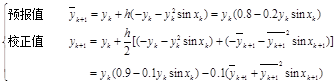
当![]() =0,x0=1, y0=1时,x1=1.2,有
=0,x0=1, y0=1时,x1=1.2,有
![]()
![]()
当![]() =1,x1=1.2, y1=0.71549时,x2=1.4,有
=1,x1=1.2, y1=0.71549时,x2=1.4,有
![]()
![]() =0.52608
=0.52608
3:写出用四阶龙格-库塔法求解初值问题![]() 的计算公式,取步长h=0.2计算y(0.4)的近似值。至少保留四位小数。
的计算公式,取步长h=0.2计算y(0.4)的近似值。至少保留四位小数。
解 此处f(x,y)=8-3y, 四阶龙格-库塔法公式为
![]()
其中 k1=f(xk,yk);k2=f(xn+![]() h,yk+
h,yk+![]() hk1);k3=f(xk+
hk1);k3=f(xk+![]() h,yn+
h,yn+![]() hk2);k4=f(xk+h,yk+hk3)
hk2);k4=f(xk+h,yk+hk3)
本例计算公式为:![]()
其中 k1=8-3 yk;k2=5.6-2.1 yk;k3=6.32-2.37yk; k4=4.208+1.578yk

当x0=0,y0==2,
![]()


