本节运用公理化的原理和要求，同时参照经典的希尔伯特公理系统，对现行中学几何课本的公理设置、原始概念、逻辑要求及公理体系存在的优缺点等进行分析、对比，在较高的观点下，把握中学几何的基础和特点。

一、中学几何属于欧几里得几何范畴

中学几何知识是几何中最基础的部分，是人们生活、学习、进一步研究几何和数学，以及从事生产劳动及许多科学技术研究都离不开的基础知识。现在的中学几何内容是在过去许多几何教材的基础上，根据我国现在中学生的知识水平及国民经济建设得实际需要。遵照我国教育的总体要求，经过反复研究确定下来的。

中学几何是以欧几里得《几何原本》为原型建立的。其方法采用了欧几里得实体公理化方法，即以不完备的公理系统加上一些直观承认的客观事实为基础，通过逻辑推理建立演绎体系，其内容基本上是《几何原本》的内容。

这里提到的中学几何是指现行九年义务教育的平面几何和立体几何课本。

二、中学几何的原始概念

原始概念是几何所讨论的原始对象和关系，是没有定义的，但其属性由公理来确定。

1.原始元素：点、线、面、体。

点  标记一个位置，是空间中位置的抽象，是构成图形最基本的元素。

线  有直线和曲线，是面的界。线和线交于点。

面  有平面和曲面，是体的界。面和面相交于线。

体  是几何体的简称。对于一物体，当它的形状、大小而不考虑其它性质时，我们就说它是几何体。即体是客观物体的抽象。体由面围成，即它的界是面，面和面相交成棱（线），棱和棱交于点。体是点、线、面按着一定条件组合而成的，当点、线、面组合的条件变了，体也随着发生了变化，由一种体转化成另一种体；反过来，点、线、面依附于体而存在，体决定了它们的组合关系，这就是点、线、面、体的相互联系、相互制约、相互转化的对立统一关系。

点、线、面或若干点、线、面组合在一起，就成为几何图形。在同一平面内的几何图形叫做平面图形，如直线、平行线、角、多边形、圆等；不在同一平面内的几何图形叫做空间图形，如平面、平行平面、二面角，以及各种几何体等。

初等几何学就是研究各种几何图形及其性质的。初等几何学所研究的几何图形一般是比较规则和比较简单的，在平面图形中除了圆以外，主要讨论直线组成的直线形；在空间图形中除了旋转体以外，主要讨论平面组成的平面形。因此，在初等几何学中，点、直线、平面才是主要的原始元素。

直线  "一根拉紧的线；一张纸的折痕"都给我们以直线的形象，"直线是向两方无限延伸着的"，"一条直线上有无限多个点"。这些描述都不是给直线下定义，而仅仅是直观的、形象的描述。直线虽无定义，但它的一些基本属性受公理的制约。如第一条公理：“经过两点有一条直线，并且只有一条直线。”这样，使直线和曲线区别开来，说明它是“直”的线而且两端可无限延长，还要满足其它关于直线的公理。

平面  高中立体几何课本中给出平面的直观描述，如“常见的桌面、黑板面、平静的水面以及纸板等，都给我们以平面的形象”，“几何里的平面是无限延展的”。平面虽无定义，但它的一些基本属性受公理的制约。如立体几何教材中的公理1：“如果一条直线上的两点在一个平面内，那么这条直线上的所有点都在这个平面内。”这说明平面是“平展”的而且可以无限延展，从而使平面与其它曲面区别开来；又如公理2：“如果两个平面有一个公共点，那么它们有且只有一条通过这个公共点的直线。”这一公理一方面说明平面的特性，另一方面说明几何空间不能高于三维（否则两个平面就可能交于惟一一个点），再加上我们承认平面外存在无限多个点，从而肯定了立体几何是三维空间的几何学；再如公理3：“经过不在同一直线上的三点，有且只有一个平面。”这也说明平面特性。这样一来，平面虽没有定义，但通过公理明确它的基本属性。

2.原始关系： 结合关系、顺序位置关系、运动关系、度量关系

结合关系  这个关系通过术语“在...上（内）”，“连接...”，“经过...”等来表达，也就是点、线、面、体间的属于、关联的关系。它们的意义一般通过公理来制约。

顺序位置关系  这个关系通过术语“两点间的部分”，“延长”，“同侧”，“不同侧”，“内部”，“外部”等表达。顺序位置的意义没有相应的公理来制约，主要靠图形的直观。如：“在直线上某一点一旁的部分叫做射线”，“直线上两点间的部分叫做线段”，“在 的内部”等。

运动（移动）关系  这个关系用术语：“重合”，“移到”，“沿...落下”，“绕...旋转”等表达。如：“把线段 放到线段 上，使点 和 重合。”，“能够完全重合的两个图形叫做全等形。”，“一条射线 由原来的位置，绕着它的端点 旋转到另一个位置”等。运动的几何性质在课本中没有相应的公理来制约，可以当作物理中的运动，直观地承认下来。

度量关系  这个关系用术语“线段的长度”，“角的度数”，“，面积”，“体积”来表达。如“度量线段的长度”，“连接两点线段的长度叫做两点间的距离”，“一个角的度数是...”，“多边形的面积就是它所围成的平面部分的大小”（这不是面积的定义，只是对面积的直观描述）等。"长度”，“角度”没有相应的公理来制约，面积在小学算术里已经讲过，其基础是矩形面积等于长与宽之积，“体积”设有两条公理，说明长方形的面积与长方体的统计与线段（边、棱）长度的关系。

原始概念是一切定义的基础，因此有了上述的原始原素和原始关系，就可以在公理允许的范围内定义其它图形和几何关系。如三角形、圆、棱柱、球、以及平行、垂直、全等、相似等等。

中学课本把直线、射线、线段和角看作是“基本概念”或“基本图形”，这个基本概念和原始概念（也称为基本概念）的意义是不同的，因为在公理化的欧几里得几何学中，线段和角是有定义的。

由于中学几何的公理不足，不能全部规定原始原素和原始关系的基本属性和意义，有的要靠直观，因此课本中没有明确哪些是原始概念，也不要求执教者在教学中严格划分，但教师应该心中有数，以便正确地进行概念的讲授。

三、中学几何学的公理系统

公理是建立几何学的基础，如何设置中学课本的公理是十分重要的问题，它既不改动从中学生的实际出发，又要适应论证推理的要求。

现行中学课本共设置了15条公理，其中初中平面几何的公理共计9条，高中立体几何的公理共计6条。

1．平面几何公理

公理1 经过两点有一条直线，并且只有一条直线。

公理2 在所有连结两点的线中线段最短。

公理3（平行公理） 经过直线外的一点，有且只有一条直线和这条直线平行。

公理4 两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行。

公理5    两条平行线被第三条直线所截，同位角相等。

公理6（边角边公理） 有两边和它们的夹角对应相等的两个三角形全等。

公理7（角边角公理） 有两角和它们的夹边对应相等的两个三角形全等。

公理8（边边边公理） 有三边对应相等的两个三角形全等。

公理9（斜边、直角边公理） 有斜边和一条直角边对应相等的两个直角三角形全等。

2．立体几何公理

公理10 如果一直线的两点在一个平面内，那么这条直线上所有点都在这个平面内。

公理11 两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

公理12 经过不在同一直线上的三点，有且只有一个平面。

公理13 平行于同一直线的两条直线互相平行。

公理14 长方体的体积等于它的长、宽、高的积。

公理15（祖暅原理） 夹在两个平行平面间的两个几何体，被平行于这两个平面的任一平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等。 

全部15条公理，可以根据其作用分成5类：

(1）结合公理组：公理1、10、11、12

公理1是点、直线的结合关系，既肯定了过两点的直线的存在性，又肯定了它的惟一性，从而确定了直线的特性，使直线与曲线区别开来；

公理10、11、12是确定点、直线、平面间的结合关系。

(2）平行公理组：公理3、4、5、13

公理3是体现欧几里得几何特点的公理；

公理4是判定平行线的公理，通过它可以做平行线；

公理5是平行线的基本性质；

公理13肯定了空间平行线的传递性。

(3）合同公理组：公理2、6、7、8、9

公理2一方面通过线段的局部性质说明线段的整体性质，即通过两点间所连接的线中直线段最短，揭示了直线的“直”的特性；另一方面反映了从一个位置到另一个位置的所有路径中，“直”的路径最短的客观规律，从而指出两点间距离的特征。但是在欧几里得学的希尔伯特公理体系中，这一公理不过是合同公理的一个推论，在中学几何中，这条公理主要作用也是比较图形大小，如它首先推出的是“三角形任意两边之和大于第三边”的定理，根据这两个理由，这里把它列入合同公理组中。

公理6、7、8、9是三角形合同的判定公理，三角形合同的性质在中学几何里有较多应用。

(4）体积公理组：公理14、15

公理14肯定了长方体的体积 ，这是建立体积理论的基础。根据公理14、15，可以通过割、补、分、和等办法，首先推出棱柱的体积等于它的底面积 和高 之积，即。再依据公理15进一步推得了 “等底面积等高的两个棱锥体的体积相等”，然后将三棱柱剖分成等底面积等高的三个三棱锥，从而得出三棱锥体积，以及棱锥体积、棱台体积，最后逐步推导出圆柱、圆锥、圆台、球等的体积。实际上公理14、15也是扩大到公理，这是因为她们本身是可以证明的，只是证明过程很复杂，还要用到极限的概念，这种证明以及超过了中学生知识储备范围，故在中学几何学中将它们作为公理。

采用公理15（祖暅原理）解决体积问题，即方便又简化了推导过程。

    

4）中学几何的公理系统不具有独立性

中学几何的公理系统是采取扩大公理系统的方法，把一些本来作为定理的一些命题作为公理提出了。

例如公理5是可以证明的命题。 

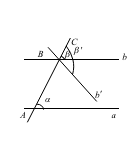
公理5 两条平行线被第三条直线所截，同位角相等。

已知直线，直线与相交于点和。同

位角和（如图）。求证：。

假设。过存在直线，使、构成的同

位角，且与不同。

根据公理4，，于是过有两条直线和同时平

行于，这与平行公理3矛盾，因此，证毕。

公理7（角边角公理），公理8（边边边公理），公理9（斜边、直角边公理）在希尔伯特公理体系中，都是公理6（边角边公理）即合同公理III₅  的推论，故它们都是可以证明的。

中学几何选取扩大公理的方法，原因有二。第一，把定理作为公理来用，可以减少许多繁琐的证明，精简教材的篇幅，满足少而精的原则；第二，初中一年级的学生年龄小，知识水平有限，理解和接受能力较差，用扩大公理的方法，可以降低知识的难度，容易学，这并不影响逻辑推理能力的培养。

  五、中学几何的公理系统不具有完备性

尽管中学几何课本采取扩大公理的方法，但公理仍然不够用。

中学几何的公理1相当于希尔伯特公理系统的结合公理I₁和公理I_2，但缺少公理I_3.

中学课本使用了“两点在...之间”，“同旁（侧）”，“不同旁（侧）”，“内部”，“外部”，同时也承认直线上点是稠密而有序的，承认图形可将平面分成不同部分（区域）等等，但并没有相应的公理来明确这些概念的意义，以及证明直线上点的稠密有序性、图形划分平面为不同区域等。希尔伯特为解决点在直线上的顺序，以及点在平面、空间的位置关系等，设置了一整套顺序公理作为依据，进行一系列的定义和推导，而这些在中学几何课本里要靠直观的图形来承认。

中学课本通过“把...移到...上面”，“沿...方向落下”，“重合”，“叠合”等不定义的基本关系来定义线段相等和角相等，进行线段大小和角的大小的比较。例如“比较两条线段 和 的长短，也可以把它们移到同一条直线上，使一个端点 和 重合，另一个端点  和 落在直线上 的同侧。如果点 和 重合，就说明线段 和 相等，记作 ；如果点在线段 上，就说明 大于 ，记作 ；如果点 在线段 以外，就说明线段 小于 ，记作 ”。

中学课本在规定线段相等或角相等时，没有相关的公理来制约，而希尔伯特公理体系中，提出合同公理Ⅲ1-4，才建立线段、角的相等。

线段和角的度量是一个十分重要的概念和理论，在希尔伯特公理体系中，是通过连续公理来建立线段、角的度量，并为了解决度量问题进行了一系列地推导；中学几何课本也在第一章中先后提出了线段的度量和角的度量问题，是结合直刻度尺和量角器的功能提出的，是直观给出，但并没有在其公理体系中给出线段度量公理和角的度量公理，即直刻度尺公理和量角器公理。

以上举例，说明中学课本中所设置的公理是很不够用的。在建立严格的欧几里得演绎体系中，所缺少的这些公理并不是可有可无的，而是必须具有的。只不过，在中学课本中并没有把它们用明确的条纹规定下来，而是通过图形或常识，直观地，不成文地承认下来，并在需要的时候，直接应用它们。这就是古典公理法（实体公理法）建立几何系统时的特点。

用实体公理化方法建立中学几何的演绎体系是最现实的、可行的、恰当的方法。