知识点一:平面到平面上的平行射影
设
![]() 和
和![]() 是两个不同的(平行或相交)的平面,
是两个不同的(平行或相交)的平面,![]() 是不平行
是不平行![]() 也不平行
也不平行![]() 的直线。
的直线。
定义:![]() 到
到![]() 沿方向
沿方向![]() 的平行射影,指的是从
的平行射影,指的是从![]() 到
到![]() 的一个映射,它使得平面
的一个映射,它使得平面![]() 上的每个点
上的每个点![]() 对应于
对应于![]() 上的点
上的点![]() ,点
,点![]() 在过点
在过点![]() 且平行于给定直线
且平行于给定直线![]() 的直线上,
的直线上,
如图所示

平行射影把平面![]() 上的一个图形
上的一个图形![]() 变成平面
变成平面![]() 上的某个图形
上的某个图形![]() 。
。
如果![]() ,则平行射影把
,则平行射影把![]() 上的图形变成
上的图形变成![]() 上的一个全等的图形;如果
上的一个全等的图形;如果![]() ,则平行射影改变图形的形态。
,则平行射影改变图形的形态。
改变直线![]() 的方向,会得到不同的从
的方向,会得到不同的从![]() 到
到![]() 的平行射影。
的平行射影。
平行射影具有以下基本性质:
性质1
平行射影把![]() 上的直线映射成
上的直线映射成![]() 上的直线(图1).
上的直线(图1).
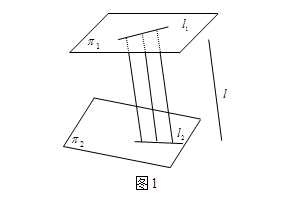
实际上,过直线![]() 上的点且平行于
上的点且平行于![]() 的直线构成一个平面
的直线构成一个平面![]() ,
,
![]() 在上述平行射影下的像就是平面
在上述平行射影下的像就是平面![]() 同
同![]() 的交线;
的交线;
反之,![]() 上的每一条直线都是
上的每一条直线都是![]() 上某一直线的像。
上某一直线的像。
性质2 平行射影把平行直线变成平行直线(图2).
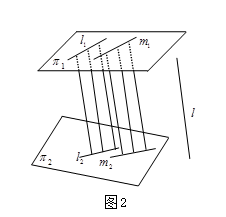
实际上,作与直线![]() 平行且分别通过
平行且分别通过![]() 与
与![]() 的两个平面
的两个平面![]() 和
和![]() ,
,
则平面![]() 和
和![]() 平行,
平行,
从而![]() 与
与![]() 与平面
与平面![]() 的交线
的交线![]() 与
与![]() 也平行。
也平行。
性质3 平行射影保持两条共线的线段的长度之比不变,也保持平行线上两个线段的长度之比不变。
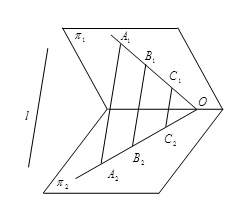
实际上,与一个角的两边相交的平行线在这两个边上截得成比例的线段![]()

设![]() 上
上![]() ,并设
,并设![]() 是直线
是直线![]() 上的点,使得
上的点,使得![]() ,
,
有性质2知,平行射影将![]() 变成
变成![]() ,
,
故有上面已证,有![]()
即![]() 。
。
性质4 平行射影保持平面上两个图形的面积比不变。
定理1
设![]() 是平面
是平面![]() 上不共线的三个点,
上不共线的三个点,![]() 是平面
是平面![]() 上不共线的三个点,则存在从
上不共线的三个点,则存在从![]() 到
到![]() 上的一个平行射影把
上的一个平行射影把![]() 映射成
映射成![]() 上与
上与![]() 相似的
相似的![]() .
.
证明 一般情况即![]() ,将平面
,将平面![]() 与
与![]() 放置于空间中,使得
放置于空间中,使得![]() 与
与![]() 沿直线
沿直线![]() 相交,
相交,
在平面上![]() 选取一点
选取一点![]() ,使得
,使得![]() ,则所求的平行射影由直线
,则所求的平行射影由直线![]() 确定.
确定.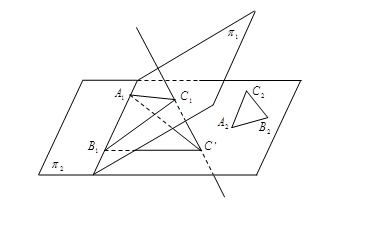
例1.设![]() 是
是![]() 的三条高线,则有
的三条高线,则有![]()
证明:因为![]() ,所以
,所以![]() ,
,
同理可得![]()
![]() ,
,
于是![]()
![]() 。
。
例2.设![]() 分别是
分别是![]() 的边
的边![]() 上的点(不在延长线上),如果
上的点(不在延长线上),如果![]() ,则直线
,则直线![]() 共点
共点
(证明思路)我们求得一个平行射影,将![]() 所在的平面
所在的平面![]() 映射的另一个平面
映射的另一个平面![]() 上得到
上得到![]() ,使得直线
,使得直线![]() 在平行射影下的象是
在平行射影下的象是![]() 的三条高线
的三条高线![]() ,这样由例1可得给定的等式。
,这样由例1可得给定的等式。
证明 做![]() ,使得三条高线
,使得三条高线![]() 的垂足依次分三边
的垂足依次分三边![]() 为给定比:
为给定比:![]() ,做法如下:
,做法如下:
首先,取任意线段![]() ,在
,在![]() 上取点
上取点![]() ,使得
,使得![]() ,过点
,过点![]() 做线段
做线段![]() 的垂线
的垂线![]() ,在线段
,在线段![]() 上取点
上取点![]() ,使得
,使得![]() ,过
,过![]() 做
做![]() 的垂线
的垂线![]() ,设以线段
,设以线段![]() 为直径的半圆与垂线
为直径的半圆与垂线![]() 的交点为
的交点为![]() 。直线
。直线![]() 与垂线
与垂线![]() 的交点为
的交点为![]() ,连接
,连接![]() 得
得![]() 。
。
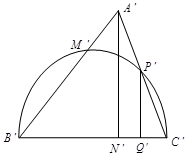
下面证明![]() 为所求作的三角形。
为所求作的三角形。
![]() 和
和![]() 是
是![]() 中
中![]() 边上的高线,设
边上的高线,设![]() 是另外一条高线。
是另外一条高线。
由于![]() ,
,![]() ,
,
并且由例1知:![]()
而![]()
所以![]()
由定理1,用一个平行射影将![]() 映射到和
映射到和![]() 相似的一个三角形
相似的一个三角形![]() 。
。
由平行射影性质3:“平行射影保持共线线段的比不变”,可知点![]() 映射到
映射到![]() 的高线的垂足上。
的高线的垂足上。
而直线![]() 则映射到它的高线上,由于三角形的高线共点,故
则映射到它的高线上,由于三角形的高线共点,故![]() 共点。
共点。
