一、中心射影的定义

首先介绍直线到直线的中心射影：

设与是同一平面内两条不同的直线，是在此平面内不在与上的一点。从 把直线 射影到直线 上，即直线上任意一点，对应于直线上属于连线上的点，这样定义的映射直线 到直线上的中心在点的中心射影，称也叫做在上的中心射影，称为射（投）影线，称为射（投）影中心，（见图1）

显然也叫做在上的中心射影。 

从定义可知，中心射影与射影中心的位置有关。

若与相交于，那么在中心射影下，是自对应点，称为中心射影下的二重点。

在平面内两条相交直线间的中心射影中，上有一点，连线与平行，故与无交点，在上没有中心射影，称为影消点。同样在上也有一点，连线与平行，在上也没有投影点，称为中的影消点。因此，此中心射影在与间不是一一对应。

下面介绍平面到平面的中心投影：

设与是两个不同的平面（见图2），在这两个平面之外选一点，对上任意一点，连接交平面于点，这样定义的映射称为从平面到平面的中心在 的中心射影，称点为点在上的中心射影，称为射影中心，称为射（投）影线。

显然，也称为在上的中心射影。

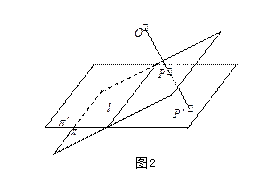
从定义知，中心射影与射影中心的位置有关。

易知，在中心射影下，平面内的直线对应内的直线。当与相交于直线时，交线上的每一点都是自对应点，交线称为中心射影下的二重直线。

在两个相交平面间的中心射影中，过点做平行于的平面，与有一条交线，则这条交线上的点，在中没有射影点，称之为上的影消线。同样，在上也有一条直线，在上没有射影像，称之为的影消线。故平面之间的中心射影也不是一一对应。

二、无穷远元素

上面已经看到，中心射影不是一一对应，下面在直线上引进一个新点，使平行的直线有且只有一个交点；在平面上，对任何一组平行直线引入一个新点，叫无穷远点。此点在这组直线中的每一条上，于是平行的直线交于无穷远点。无穷远点记为，平面内原有的点叫做有穷远点。

所有相互平行的直线上引入的无穷远点是同一个无穷远点，不同的平行直线组上引入不同的无穷远点。

由于每一条直线上只有一个无穷远点，于是平面上引入的所有无穷远点的集合的轨迹与平面内的每一条直线有且只有一个交点。

因此，规定这个轨迹是一条直线，称为无穷远直线，记为，平面内原有的直线叫做有穷远直线。

在欧氏直线上添加了无穷远点之后，便得到一条新的直线，叫做仿射直线。若将直线 上的有穷远点与无穷远点不加区别，等同看待，则这条仿射直线叫做射影直线。

下面给出一个模型来解释射影直线。

以一个单位圆，与直线相切于（见图5），记的对径点为。任取连接交直线于点，这样就建立了与之间的一一对应。可以看出，当趋于时，趋于。规定对应于，从而可以认为射影直线是封闭的，它上面的点与单位圆上的点一样多，要同等对待有穷远点与无穷远点，就像同等对待圆周上的任何两点一样。

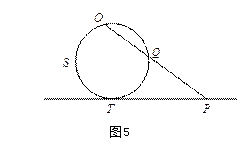
同样，将上面的概念拓广到平面上，平面上添加一条无穷远直线，得到的新的平面叫做仿射平面。若对仿射平面上无穷远元素（无穷远点、无穷远直线）与有穷远元素（有穷远点、有穷远直线）不加区别，同等对待，则这个平面称为射影平面。

空间中添加了很多无穷远点，所有这些无穷远点的轨迹可以认为是一个平面，称为无穷远平面，记作

平行的两个平面相交于无穷远直线上，任何一个平面与无穷远平面相交于无穷远直线上，一条直线与平行平面相交于一个无穷点。

在仿射平面上，任何两条直线有并且只有一个交点。两条有穷远直线若不平行则交于有穷远点，若平行则交于无穷远点，任意一条有穷远直线与无穷远直线交于无穷远点。

三、透视对应与中心透视

如图1，在引进无穷远元素之后，通过中心射影，把上影消点投影到上无穷远点，把上的无穷远点投影到上影消点。于是中心射影建立了直线之间的一一对应，称这个中心射影为直线间的透视对应

同理，中心射影把平面上的影消线投影到上无穷远直线，同时把上的无穷远直线投影到上影消线。于是中心射影建立了平面到平面间的一一对应，称为平面与之间的中心透视。

（下面看一下中心射影如何改变线段的长度）

设是平面上的一个线段，在以为中心的中心射影下，在上的像是

如图6所示

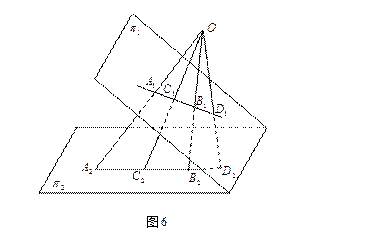
由三角形的面积公式可知（具有公共角的两个三角形的面积之比等于夹这个角的两边的乘积之比）

设与分别是点到直线与的距离，

则有

或者

若是中直线上的三个点，而是上对应的投影像，则从上面公式可得        （1）

上式表明：在中心射影下比值一般不等于比值

 

但是对直线上的两点，设为其在上的投影像，则有           （2）

即与分别分割线段所得到的有向线段的比（交比）在中心射影下保持不变。

 

定理1  设是平面上的四个点，其中任何三点不共线，是平面上的任何三点不共线的四个点，则存在从到的中心（或平行）射影，它把四边形变成与四边形相似的四边形

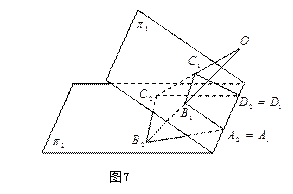
证明  如图7所示

在平面上做与四边形相似的四边形，使得，

在空间中移动，使与交于直线，

连接，则直线共面，

故与的交点就是所求中心射影的射影中心（如果与平行，则所求中心射影为平行射影）。

定理2    设是平面上任意一个多边形，是它的边上或边的延长线上的点，则下面的乘积在中心射影下保持不变。

证明  设与分别是点和在以为中心的中心射影下的像，则由（1）式有：

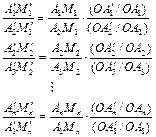
将这些等式两端对应乘积得。

四、球极中心射影

（中心射影也可以用来解决包含圆的有关初等几何问题）

设是一球面，是球面上的一点，从球面到它在点处的切平面上的球极平面射影，就是中心在点（点的对径点）的从到的中心射影。

在球极平面射影下，上的任一点（）的像是直线与平面的交点，而点在平面上没有像。

球极平面射影的性质：

性质1  球极平面射影把球面上的每一个圆变成平面上的一个圆或一条直线，反之，上的圆或直线的原像是上的圆

性质 2  设是平面上的一个圆，是上的不与圆相交的直线，则存在从平面到某个平面的中心射影。它把变成上的圆，并且把直线变成上的无穷远直线。

证明  如图9所示，经过圆在空间做一个球面，并过作一个与球面某点相切的平面。设是平行于平面并与球面相切于点的平面，则与是对径点。

则以为中心的从平面到平面的中心射影，将圆映为平面上圆。将直线映成无穷远直线。

性质3  设是平面上的一个圆，是圆内部的一点，则存在从平面到某一个平面上的中心射影，它把变成平面上的圆。并且把点变成圆的中心。