在欧氏直线上规定好原点和正方向后，每一个有穷远点与一个实数(笛卡尔坐标，简称为笛氏坐标）相对应，但无穷远点 就没有坐标，而 不是数，不能作为坐标。为了描述无穷远点，引进齐次坐标。

1.一维齐次坐标

定义1    设欧氏直线上的有穷远点 的笛氏坐标为 ，则满足 的有序数对 ，叫做点 的齐次坐标，记为 。

规定 时， 或 为直线上无穷远点的齐次坐标。

由定义知：

（1）不同时为0的有序数对 ，确定惟一一个点 ， 不是点的齐次坐标；

（2）齐次坐标不是惟一的，若 ，则 与 表示同一个点的齐次坐标；

（3）当时 ， 是有穷远点， 时 是无穷远点， 称为 的非齐次坐标，无穷远点没有非齐次坐标。

2.二维齐次坐标

定义2    设欧氏平面 内点 的笛氏坐标为 ，则满足 的有序三元数组 叫做点 的齐次坐标，记为 ；

为区别起见， 叫做点的非齐次坐标。

下面说明无穷远点的齐次坐标：平面内平行的直线束，交于同一个无穷远点，而这族平行直线中一定有一条过坐标原点，设它的方程为 ， 是直线的斜率，取这组直线上无穷远点的齐次坐标为 ；当 时，直线是 轴， 就是 轴上无穷远点的齐次坐标；当 时，直线是 轴， 表示 轴上无穷远点的齐次坐标。

若 ，则 与 是同一个无穷远点的齐次坐标。

由上述知： 不表示一个点的齐次坐标； （ 不同时为0）是一个无穷远点的齐次坐标； 是一个有穷远点的齐次坐标。

3.齐次坐标下的直线方程

在笛卡尔直角坐标系下，设直线的方程为

其中直线上点 的非齐次坐标 是 ，齐次坐标为 ，则 ，

于是 ，即 ，

上式就是直线的齐次方程。

注意：（1）过原点的直线的齐次方程为 ；

     （2）无穷远直线的齐次方程为 ；

     （3）无穷远直线无非齐次方程。

4.直线的齐次线性坐标

在齐次点坐标中，直线的齐次方程为 ,

其中 是直线上点的齐次坐标，直线由三个系数 惟一确定;

若 ，那么 与上面的方程表示同一条直线.

定义3    直线的齐次方程中 的系数 叫做直线的齐次线坐标，记为 。

注意：

（1）  若 ， 也是直线的齐次线坐标,故直线的齐次线坐标不惟一.

（2）  是 轴的齐次线坐标， 是 轴的齐次线坐标， 无穷远直线的齐次线坐标。

综上，我们得到如下定理：

定理1  一点 在一直线 上的充分必要条件为 。

若直线 不通过原点，则当 时，称 为直线 的非齐次坐标。

所有不通过原点的直线的方程都可以写成

定理2    两个点 的连线的齐次方程为 ，

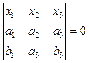即 。

证明    设 两点的连线的齐次方程为 ，其中 是待定系数，于是 ， ，

上面三个方程写成矩阵的形式为 ，

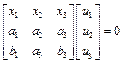这个式子可以看成是该直线的齐次线坐标 所满足的齐次线性方程组，所以该方程组有非零解，当且仅当系数行列式为零，

即 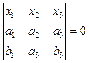，这就是连线的方程