二次曲线是平面解析几何的主要研究对象，通常通过坐标变换得出曲线的标准方程来讨论其几何性质。

一、坐标变换

平面上点的坐标与建立的坐标系有关，同一个点在不同坐标系下有不同的坐标，研究不同坐标之间关系就是坐标变换的问题。

设平面有两个不同的坐标系 与 ，平面上任意一点 在这两个坐标系下的坐标分别为 与 。

在欧氏几何里，从坐标系 到 可以看成是经过一个正交变换（运动）得到的，如果两个坐标系为同向的（同是右手系）。因此可以把运动分解为平移和绕点旋转的乘积。

设平移 将坐标系 变成 ，点 在原坐标系 中的坐标为 ，点 的原坐标与在 中的新坐标之间的关系为：

即 ；

设以点 为中心，逆时针方向旋转角 的旋转变换记为 ，将坐标系 变成 ，点 在 的坐标与在 的坐标之间的关系为：

；

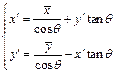两个变换的积 将原坐标 变成新坐标系 ，其公式为：

这就是先平移后旋转的一般坐标变换公式。

坐标变换也可以用原坐标来表示新坐标，其公式为

这实际上是上述变换的逆变换，是先将坐标系 顺时针旋转角 ，然后再平移到点 （这是点 在 下的坐标）而得到的。

二、坐标变换与点变换

坐标变换是研究同一点在两个不同坐标系下坐标之间的关系，即研究点在坐标系变换下其坐标的变化规律。点变换是研究在同一坐标系下，点与其变换后的对应点坐标之间的关系。

在欧氏平面上，设直角坐标系 经过第一种正交变换变成直角坐标系 ，一点 在原坐标系的坐标为 ，在新坐标系的坐标为 ，则坐标变换公式

为               eq \o\ac(○,1)1

对于点变换来说，设在同一个第一种正变换之下，点 变成点 ，设点 ， 在同一个直角坐标系 的坐标分别为 和 ，则第一种正交变换公式

为                 eq \o\ac(○,2)2

分析：坐标变换公式 eq \o\ac(○,1)1和刚体运动公式 eq \o\ac(○,2)2是一致的。

区别是：从形式上看，两个公式中的 和 在等号两边互换一个位置，又 在两个公式里的意义有差别，前者表示点 在新坐标系 的坐标，后者表示点 在原坐标系 下的坐标。如果作如下解释，这个差别也是可以统一的。实际上，点 在坐标系 的坐标为 ，在坐标系 的坐标为 ，则点 关于两坐标系 和 的坐标变换公式正好是 eq \o\ac(○,2)2。这说明点变换 eq \o\ac(○,2)2也是坐标变换，它与坐标变换 eq \o\ac(○,1)1反向。

我们可以通过坐标变换来化简曲线的方程，只需将原坐标系通过移轴和转轴移到与曲线相关的位置就可以达到目的；也可以通过点变换来化简曲线方程，只需将曲线经过刚体运动移到与坐标系相关的位置就可以达到目的。

三、坐标变换下的不变性质和不变量

通过方程研究曲线的几何性质是解析几何的重要任务之一，然而曲线方程与建立的坐标系有关，不同的坐标系可以得出不同的方程。

例如：直线的一般方程为

如果通过坐标原点，其方程为 ，即常数项消失。

如果它与一个坐标轴平行，其方程可以变成

对于一条二次曲线的一般方程，经过坐标变换后，可以得到它的标准方程，于是可通过对标准方程的研究来得到这条曲线的几何性质。

既然同一条曲线（图形）可以由不同的方程来表示，那么这些不同的方程就应该有某些共同的东西。它们通过坐标的关系和系数的关系和量，反映了曲线本身所固有的几何性质。它们与坐标系的选择无关；反过来，只有这些共同的东西才表示该曲线的几何特征。使它与其它曲线区别开。这些共同的东西就是坐标变换下的不变性质和不变量，它们取决于变换的性质。

设二次曲线的方程为

              （1）      

现在我们要选取一个适当的坐标系，也就是要确定一个坐标变换，使得曲线（1）在新坐标系下的方程最为简单，这就是二次曲线方程的化简。为此，我们必须了解在坐标变换下二次曲线方程的系数是怎样变化的。因为一般坐标变换是由移轴与转轴组成，所以我们分别考察在移轴与转轴下，二次曲线方程（1）的系数的变换规律。

在移轴变换 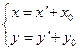下二次曲线（1）的新方程为：

           

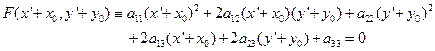
化简整理后方程记为：

                  

这里

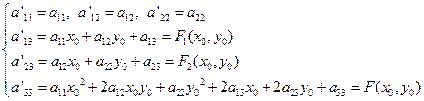            （2）

因此在移轴下，二次曲线方程系数的变换规律为：

1．  二次项系数不变

2．  一次项系数变为 与 ；

3．  常数项变为 。

在转轴变换 下二次曲线（1）的新方程记为：

          

这里

进制 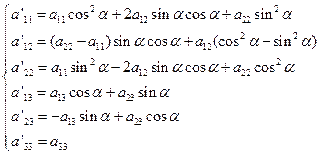      （3）

因此，在转轴下，二次曲线方程（1）的系数的变换规律为：

1）  二次项系数一般要改变。新方程的二次项系数仅与原方程的二次项系数及旋转角有关，而与一次项系数及常数项无关。

2）  一次项系数一般要改变。新方程的一次项系数仅与原方程的一次项系数及旋转角有关，与二次项系数及常数项无关。

3）  常数项不变。

 

下面简要介绍在正交变换下，曲线在坐标变换下的不变性质与不变量。

（1）．不变量与半不变量

二次曲线在任意给定的直角坐标系中的方程为

                  （1）

设在直角坐标变换(5.6-3)

          

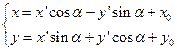
下，曲线方程（1）的左端变为

那么多项式 也是二元二次多项式，它的每一个系数都可以用多项式 的系数和坐标变换(5.6-3)的系数表出。

定义  由 的系数组成的一个非常数函数 ，如果经过直角变换(5.6-3)， 变为 时，有

              

那么这个函数 叫做二次曲线（1）在直角坐标变换(5.6-3)下的不变量。如果这个函数 的值，只是经过转轴变换不变，那么这个函数叫做二次曲线（1）在直角坐标变换下的半不变量。

定理  二次曲线（1）在直角坐标变换下， 是不变量， 是一个半不变量。

      

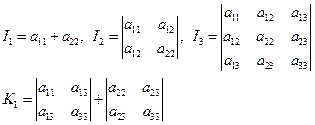
证  因为直角坐标变换总可以分成移轴与转轴两步来完成，因此定理的证明。也就分成移轴与转轴两步来完成。

先证明在移轴 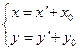下， 不变，而 一般要改变。

根据上面的讨论，在移轴下，二次曲线（1）的二次项系数不变，

所以：

        

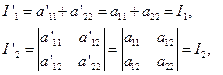
而

        

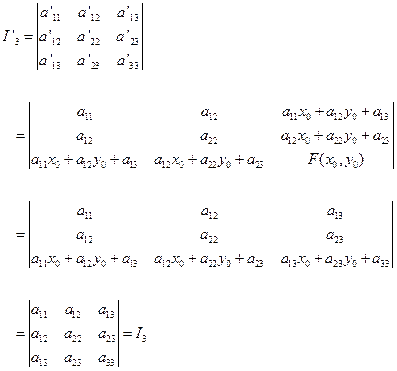
上面的第三个等式是由第三列减去第一列乘以 ，第二列乘以 而得到的，第四个等式是由第三行减去第一行乘以 ，第二行乘以 而得到的。

在移轴下一般是要改变的，例如 ，它的 ，而通过移轴变换， 变为：

          

而这时

            

               

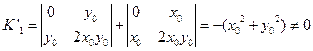
现在我们来证明转轴变换 下， 与 都不变。对于 与 只要考虑方程的二次项系数就够了，根据前面的讨论，在转轴下有

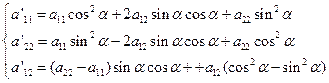                  (4)

依据三角函数关系

          

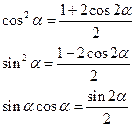
（4）可化为；

 

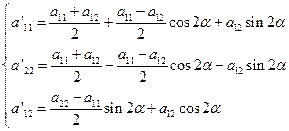
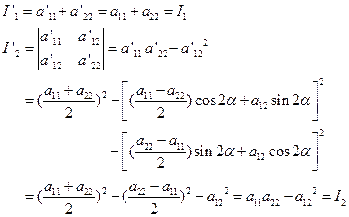
现在来证明 在转轴下也不变。因为

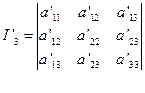
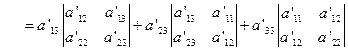
而在转轴下，刚才已证得 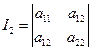不变。即 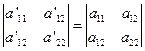，且在转轴下二次曲线方程的常数项不变，即 ，因此

          

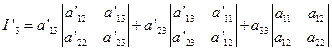
将(3)代入 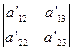，化简整理得

               

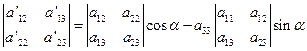
同理可得

             

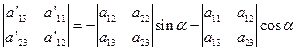
所以

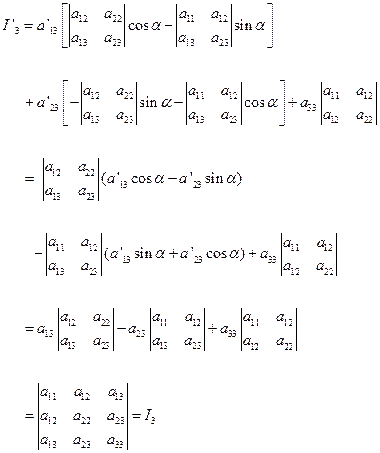
最后我们来证明 在转轴下也是不变的，因为

            

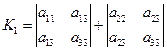
而 与二次曲线（1）的常数项 在转轴下都是不变的，又

         

所以

           

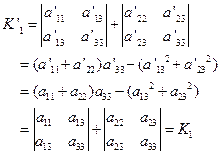
定理证毕。