一、曲线与方程

几何曲线通常是点的轨迹。

例如：平面内与两个定点 的距离和等于常数（大于 ）的点的轨迹叫做椭圆；平面内与两个定点 的距离的差的绝对值是常数（小于 ）的点的轨迹叫做双曲线；平面内与一个定点 和一条定直线 的距离相等的的点的轨迹叫做抛物线。

上述三个定义也可以归结为一个轨迹命题：

平面上与一个定点的距离和一条定直线的距离的比是常数 的点的轨迹，当 时是椭圆，当 时是双曲线，当 时是抛物线。

在解析几何里，通常把曲线 看做是适合某条件 的集合（轨迹）

现行平面解析几何课本第二章第一节“曲线和方程”中给出如下定义：

一般地，在直角坐标系中，如果某曲线 （看做适合某种条件 的点的集合或轨迹）上的点与一个二元方程 的实数解建立了如下的关系：

（1）曲线上的点坐标都是这个方程的解

（2）以这个方程的解为坐标的点都是曲线上的点

那么，这个方程叫做曲线的方程，这条曲线叫做方程的曲线

这个定义，实际上就是把前面提出的轨迹定义代数化了，关系（1）和（2）也就是定义中的“纯粹性”和“完备性”。

设曲线 是适合某种条件 的点 的轨迹（集合），即 表示 适合条件 ，据坐标法的思想建立如下对应：

点：

条件：

曲线：

上述对应表示满足的所有点 的集合与二元方程 的所有解 的集合建立了一一对应，即曲线的点集与方程的解集一一对应。

实际上，曲线方程的定义，不过是轨迹定义的几何语言转换成代数语言罢了。

给出了曲线与方程的概念以后，要具体地解决两个重要问题：一个是已知曲线求方程，另一个是已知方程画曲线。

在仿射几何、射影几何里也研究椭圆、双曲线、抛物线等二次曲线。上述定义在这两种几何里不适用，因为定义时使用了距离等度量性质，下面介绍一种在三种几何里通用的定义，即二次曲线的射影定义。

二、二次曲线的射影定义

平面上通过一点 的所有直线集合称为中心线束，记做 ，中心线束中四直线的交比定义如下：

定义  设 为中心线束 里的任意四条直线，则其交比为

其中直线称 为交比 的基础直线对，直线 称为分直线对。

定义中 表示直线 和 的夹角的正弦函数值，夹角 是有方向的，可以验证 与夹角方向的取法无关。

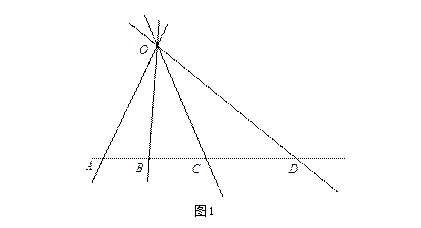
定理1  设 是以 为中心的线束中四条直线，不通过点 的任意直线 与它们依次交于 四点，则

证明  由于 ，

而上式右端恰为 ，

故 。

定理2  共点四直线的交比是射影变换下的不变量。

证明  设共点 的四直线 经射影变换后变成共点 的四直线 ，直线 截直线 的交点 变成直线 截直线 的交点 ，

则有 。

而 ，

故 。

定义  两个线束 和 的直线之间建立了一一对应，且任意四对对应直线交比总相等，即若 对应 时， ，则称这两个线束成射影对应，记作 。

定义  在平面上，两个成射影对应线束的所有对应直线 的交点的轨迹称为二阶曲线或二次曲线。

据三种几何的从属关系：射影几何 仿射几何 欧氏几何，可知这个定义同时适应于主三种几何，这个定义为研究二次曲线的射影性质、仿射性质、度量性质提供了可能性和方便条件。

导入平面的射影坐标系，可以求出二次曲线的一般的齐次坐标方程

为：

系数行列式

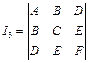
可以判断二次曲线是否退化： 是常态或非退化的； 是变态的或退化的。