知识点九:关于二次曲线的分类
通过分类来认识图形是数学中惯用的方法。一般说来,分类离不开曲线在变换下的不变性质和不变量,与变换群密切相关。
一、二次曲线的度量分类
这个分类是根据上面已经证明过的正交变换下的不变式
![]() 和半不变式
和半不变式
![]() 得到的
得到的
设二次曲线的一般方程为
![]() eq \o\ac(○,1)1
eq \o\ac(○,1)1
其中
![]() 不全为零。
不全为零。
经过坐标轴的旋转,消去
![]() 项,将方程 eq
\o\ac(○,1)1化为
项,将方程 eq
\o\ac(○,1)1化为
![]() eq \o\ac(○,2)2
eq \o\ac(○,2)2
其中
![]() 不同时为零
不同时为零
不变式为
![]()
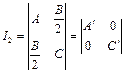 , 即
, 即
![]()
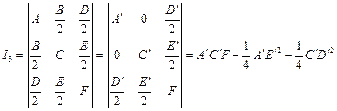
(1)当
![]() 时,
时,
![]() 从而
从而
![]() 都不为零。经坐标平移可将
eq \o\ac(○,2)2化为
都不为零。经坐标平移可将
eq \o\ac(○,2)2化为
![]() eq \o\ac(○,3)3
eq \o\ac(○,3)3
这时
![]() 和
和
![]() 的形式未变,而
的形式未变,而
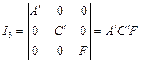
![]()
下面来看一看不变式在曲线分类时所起的作用。
1)
![]() ,则
,则
![]() ,
,
![]()
即
![]() ,
,
![]()
方程 eq
\o\ac(○,3)3中
![]() 符号相同,方程 eq
\o\ac(○,1)1称为椭圆型。
符号相同,方程 eq
\o\ac(○,1)1称为椭圆型。
当
![]() 与
与
![]() 反号时,方程为椭圆;当
反号时,方程为椭圆;当
![]() 与
与
![]() 同号时,方程 eq
\o\ac(○,1)1为虚椭圆;当
同号时,方程 eq
\o\ac(○,1)1为虚椭圆;当
![]() 时方程 eq
\o\ac(○,1)1为点椭圆,即椭圆退缩成一点。
时方程 eq
\o\ac(○,1)1为点椭圆,即椭圆退缩成一点。
2)
![]() ,则
,则
![]() ,
,
![]()
即
![]() ,
,
![]()
方程 eq
\o\ac(○,3)3中
![]() 符号相反,方程 eq
\o\ac(○,1)1为双曲线型
符号相反,方程 eq
\o\ac(○,1)1为双曲线型
若
![]() ,则
,则
![]() ,方程 eq
\o\ac(○,1)1为双曲线,若
,方程 eq
\o\ac(○,1)1为双曲线,若
![]() ,则
,则
![]() ,方程 eq
\o\ac(○,1)1为两条相交直线。
,方程 eq
\o\ac(○,1)1为两条相交直线。
(2)当
![]() 时,则
时,则
![]() ,
,
![]()
即
![]() ,
,
![]()
故
![]() 或
或
![]() 有一个为零,方程
eq \o\ac(○,1)1为抛物线型
有一个为零,方程
eq \o\ac(○,1)1为抛物线型
1)若
![]() ,
,
![]()
此时
![]()
当
![]() 时,
时,
![]() 。经过坐标轴平移,方程
eq \o\ac(○,2)2可化为
。经过坐标轴平移,方程
eq \o\ac(○,2)2可化为
![]() 式eq \o\ac(○,4)4
式eq \o\ac(○,4)4
不变式为
![]()
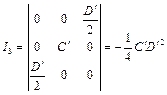
且
![]() ,
,
![]()
这时方程为抛物线。
当
![]() 时,
时,
![]() ,方程 eq
\o\ac(○,2)2可化为
,方程 eq
\o\ac(○,2)2可化为
![]() eq \o\ac(○,5)5
eq \o\ac(○,5)5
此时进行移轴变换,方程 eq \o\ac(○,5)5变为
![]() eq \o\ac(○,6)6
eq \o\ac(○,6)6
此时半不变量
![]() 时,
时,
若
![]() ,方程 eq
\o\ac(○,6)6有两个不同的实数解,
eq \o\ac(○,1)1为两条平行直线。
,方程 eq
\o\ac(○,6)6有两个不同的实数解,
eq \o\ac(○,1)1为两条平行直线。
若
![]() ,方程 eq
\o\ac(○,6)6有两个相同的实数解,
eq \o\ac(○,1)1为两条重合的直线。
,方程 eq
\o\ac(○,6)6有两个相同的实数解,
eq \o\ac(○,1)1为两条重合的直线。
若
![]() ,方程 eq \o\ac(○,6)6没有实数解, eq
\o\ac(○,1)1为两条虚实线,或说没有轨迹。
,方程 eq \o\ac(○,6)6没有实数解, eq
\o\ac(○,1)1为两条虚实线,或说没有轨迹。
2)若
![]() ,
,
![]()
此时
![]()
当
![]() 时,
时,
![]() 。经过坐标轴平移,方程
eq \o\ac(○,2)2可化为
。经过坐标轴平移,方程
eq \o\ac(○,2)2可化为
![]() 式 eq \o\ac(○,7)7
式 eq \o\ac(○,7)7
不变式为
![]()
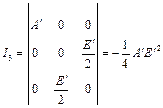
且
![]() ,
,
![]()
这时方程为抛物线。
当
![]() 时,
时,
![]() ,方程 eq
\o\ac(○,2)2可化为
,方程 eq
\o\ac(○,2)2可化为
![]()
进行移轴变换,方程(8)变为:
![]()
此时半不变量
![]() ,
,
若
![]() ,方程(9)有两个不同的实数解,
eq \o\ac(○,1)1为两条平行直线。
,方程(9)有两个不同的实数解,
eq \o\ac(○,1)1为两条平行直线。
若
![]() ,方程(9)有两个相同的实数解,
eq \o\ac(○,1)1为两条重合的直线。
,方程(9)有两个相同的实数解,
eq \o\ac(○,1)1为两条重合的直线。
若
![]() ,方程(9)没有实数解,
eq \o\ac(○,1)1为两条虚实线,或说没有轨迹。
,方程(9)没有实数解,
eq \o\ac(○,1)1为两条虚实线,或说没有轨迹。
这就是根据二次曲线方程的不变式对二次曲线进行的分类。这种分类并不把二次曲线分成等价类。如果对椭圆型不区分圆和椭圆。上述分类就是一个仿射分类;如果区分圆和椭圆为两类才是度量分类。
在解析几何里,可用离心率来划分常态二次曲线的类型。
曲线上任意一点到焦点的距离与该点到准线的距离之比,称为曲线的离心率,记作
![]() 。
。
对于有心二次曲线(椭圆、圆、双曲线)来说,离心率也是焦距(两焦点间的距离)和长轴或实轴之比。设焦距为
![]() ,椭圆的长轴或双曲线的实轴长为
,椭圆的长轴或双曲线的实轴长为
![]() ,则
,则
![]() 。
。
对于椭圆,
![]() ,有
,有
![]() (
(
![]() 为短半轴长)
为短半轴长)
对于双曲线,
![]() ,有
,有
![]() (
(
![]() 为虚半轴长)
为虚半轴长)
对于抛物线,
![]()
对于圆,
![]() 。实际上,如果把椭圆长轴固定,改变焦距使两个焦点无限靠近。以至于两者重合,则焦距
。实际上,如果把椭圆长轴固定,改变焦距使两个焦点无限靠近。以至于两者重合,则焦距
![]() 。因为
。因为
![]() ,故
,故
![]() ,椭圆就变成了圆了。因此规定圆的离心率为
,椭圆就变成了圆了。因此规定圆的离心率为
![]() (焦点为圆心,准线为无穷远直线)。
(焦点为圆心,准线为无穷远直线)。
根据离心率可将常态的二次曲线划分成四大类,即椭圆类、双曲线类、抛物线类各圆类。
二次曲线的离心率不仅是正交变换群下的不变量,也是相似变换群下的不变量。
因为相似变换把一个曲线 的焦点和准线变成其对应曲线的焦点和准线,并且保持曲线上的点到焦点和准线的距离不变,即保持离心率不变。
因此离心率相等的二次曲线 都是相似的
例如:椭圆(或双曲线)经过相似变换,无非使焦距
![]() 和长轴(或实轴)
和长轴(或实轴)
![]() 按同比例伸长或缩短,同时使椭圆(或双曲线)按同一比例放大或缩小,成为相似形。
按同比例伸长或缩短,同时使椭圆(或双曲线)按同一比例放大或缩小,成为相似形。
所有圆都相似。
所有抛物线的离心率都是1,所以所有的抛物线都相似。
离心率大小,可以将常态的二次曲线划分成相似变换群下的无数个等价类:每个确定的
![]() 值决定一个等价类。类里的曲线都是相似的。
值决定一个等价类。类里的曲线都是相似的。
二、二次曲线的仿射分类
中学解析几何中,通过不变式将二次曲线分成三大类,这种分法也是仿射变换下的分类。
回顾:平面到另一个平面平行投影也称透视仿射对应。
仿射变换是有限次透视仿射对应的乘积。
在仿射变换下虽然不保持二次曲线在正交变换下的不变式
![]() 的值不变,但可以保持
的值不变,但可以保持
![]() 的符号不变,即
的符号不变,即
![]() 变成
变成
![]() ,
,
![]() 变成
变成
![]() ,
,
![]() 变成
变成
![]() ;对于
;对于
![]() 而言
而言
![]() 变成
变成
![]() ,
,
![]() 变成
变成
![]() ,即把常态的二次曲线仍变成常态的二次曲线,退化的仍变成退化的。
,即把常态的二次曲线仍变成常态的二次曲线,退化的仍变成退化的。
据
![]() 可将二次曲线分成如下三个类型的等价类:
可将二次曲线分成如下三个类型的等价类:
椭圆型
![]() 或
或
![]()
双曲线型
![]() 或
或
![]()
抛物线型
![]() 或
或
![]()
其中
![]() 为常态的,
为常态的,
![]() 为变态的,包括两相交直线,两平行直线,两重合直线,一点对。
为变态的,包括两相交直线,两平行直线,两重合直线,一点对。
仿射分类也可通过二次曲线与无穷远直线的交点个数进行分类
椭圆型:与无穷远直线没有实交点的二次曲线的全体
双曲线线型:与无穷远直线有两相个实交点的二次曲线的全体
抛物线型:与无穷远直线有一个实交点的二次曲线的全体
事实上,设二次曲线的齐次坐标方程为:
![]() eq \o\ac(○,1)1
eq \o\ac(○,1)1
无穷远直线方程为:
![]() eq \o\ac(○,2)2
eq \o\ac(○,2)2
解方程组 eq \o\ac(○,1)1、 eq \o\ac(○,2)2求交点
将 eq
\o\ac(○,2)2代入 eq
\o\ac(○,1)1得
![]()
令
![]() ,求二次方程
,求二次方程
![]() eq
\o\ac(○,3)3
eq
\o\ac(○,3)3
的根,得
![]()
如果曲线为椭圆型,则
![]() ,方程 eq
\o\ac(○,3)3有二虚根,即无穷远直线与曲线没有实交点;反过来方程
eq \o\ac(○,3)3有二虚根时,
,方程 eq
\o\ac(○,3)3有二虚根,即无穷远直线与曲线没有实交点;反过来方程
eq \o\ac(○,3)3有二虚根时,
![]() ,曲线为椭圆型。
,曲线为椭圆型。
如果曲线为双曲线型,则
![]() ,方程 eq
\o\ac(○,3)3有二实根,即无穷远直线与曲线交于二实点,齐次坐标为
,方程 eq
\o\ac(○,3)3有二实根,即无穷远直线与曲线交于二实点,齐次坐标为
![]() 和
和
![]() ;反过来 eq
\o\ac(○,3)3有二实根时,
;反过来 eq
\o\ac(○,3)3有二实根时,
![]() ,曲线为双曲线型
,曲线为双曲线型
如果曲线为抛物线型,则,
![]() 方程 eq
\o\ac(○,3)3有二相等实根,齐次坐标为
方程 eq
\o\ac(○,3)3有二相等实根,齐次坐标为
![]() ,即无穷远直线与曲线交于一点;反过来,方程
eq \o\ac(○,3)3有一虚根时,
,即无穷远直线与曲线交于一点;反过来,方程
eq \o\ac(○,3)3有一虚根时,
![]() ,曲线为抛物线型。
,曲线为抛物线型。
双曲线在无穷远处交于两点,或封闭的曲线。这从双典线与它的渐近线的关系可以直观地看出
如图所示

渐近线
![]() 在无穷远处与双曲线一支交于无穷远点
在无穷远处与双曲线一支交于无穷远点
![]() ,与另一支交于无穷远点
,与另一支交于无穷远点
![]() ,由于直线
,由于直线
![]() 有惟一无穷远点,故
有惟一无穷远点,故
![]() 和
和
![]() 是同一点
是同一点
同理
![]() 与
与
![]() 也是同一个点。
也是同一个点。
