第二章 几何变换与变换群
 知识点三:平面几何中几个常用的定理
知识点三:平面几何中几个常用的定理
这一节,我们利用本章第2节讲过的平行射影与中心射影的基本知识来证明平面几何中几个著名定理,近几年在初高中数学联赛中也常常出现与这些定理相关的几何试题。
例1 梅内劳斯(Menelaus)定理

如图1、2所示,设
![]() 分别是
分别是
![]() 的边
的边
![]() (或其延长线)上的点,则三点
(或其延长线)上的点,则三点
![]() 共线的充分必要条件为
共线的充分必要条件为
![]()
证明 将
![]() 所在平面
所在平面
![]() 中心射影到平面
中心射影到平面
![]() 上,使得在此中心射影下直线
上,使得在此中心射影下直线
![]() 是平面
是平面
![]() 上的影消线
上的影消线
![]() ,做法如下:
,做法如下:
在平面
![]() 之外取一点
之外取一点
![]() ,取平面
,取平面
![]() ,它平行于
,它平行于
![]() 与
与
![]() 确定的平面。
确定的平面。
记直线
![]() 为直线
为直线
![]() ,则在中心射影下,
,则在中心射影下,
![]() 为影消线,
为影消线,
![]() 的像是
的像是
![]() 上无穷远直线。
上无穷远直线。
必要性的证明:
点
![]() ,故它们的像
,故它们的像
![]() 分别是直线
分别是直线
![]() 上的无穷远点,
上的无穷远点,
因此有
![]()
这时
![]()
由§2.2中Th2知
![]()
充分性的证明:
若
![]() ,由上述的中心射影把
,由上述的中心射影把
![]() 映成直线
映成直线
![]() 上的无穷远点
上的无穷远点
![]() 与
与
![]() ,于是
,于是
![]()
由§2.2中Th2知
![]()
故
![]()
这说明
![]() 是直线
是直线
![]() 上的无穷远点,于是
上的无穷远点,于是
![]() 的原像点
的原像点
![]() 必在平面
必在平面
![]() 上的影消线
上的影消线
![]() 上。
上。
即点
![]() 在一条直线上。
在一条直线上。
例2 赛瓦(Ce>)定理
如图3.4所示设
![]() 分别是
分别是
![]() 的边
的边
![]() (或其延长线)上的点,则三条直线
(或其延长线)上的点,则三条直线
![]() 共点或平行的充分必要条件是
共点或平行的充分必要条件是
![]()
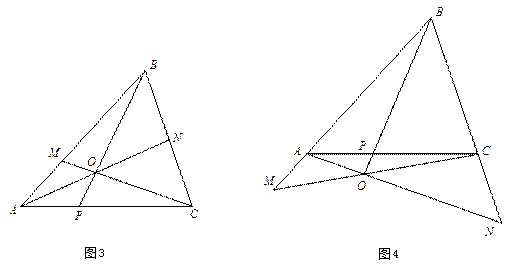
证明 仿照例1,适当地选取中心射影,将
![]() 所在平面
所在平面
![]() 映射到平面
映射到平面
![]() ,使得直线
,使得直线
![]() 是平面
是平面
![]() 上的影消线。
上的影消线。
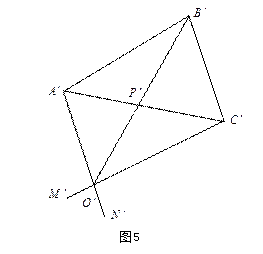
必要性的证明:如图5所示,
这时点
![]() 的像分别是平面
的像分别是平面
![]() 上直线
上直线
![]() 上的无穷远点
上的无穷远点
![]() 。
。
如果直线
![]() 相交于一点
相交于一点
![]() (或互相平行)
(或互相平行)
则必有
![]() (因为它们有公共的无穷远点
(因为它们有公共的无穷远点
![]() )
)
![]() (因为它们有公共的无穷远点
(因为它们有公共的无穷远点
![]() )
)
由已知
![]()
知
![]()
![]()
于是四边形
![]() 是平行四边形。
是平行四边形。
又据已知“直线
![]() 相交于一点
相交于一点
![]() ”,知
”,知
![]() 通过点
通过点
![]() ,故
,故
![]() 是
是
![]() 的中点,从而
的中点,从而 ![]() ,又因为
,又因为
![]() 、
、
![]() 是无穷远点,所以
是无穷远点,所以
![]() ,
,
这样
![]() ,
,
由§2.2 Th2中知
![]() .
.
充分性的证明:
假设
![]() 成立,在上述中心射影下,点
成立,在上述中心射影下,点
![]() 的像是无穷远点
的像是无穷远点
![]() ,从而有
,从而有
![]() ,
,
由§2.2 Th2知
![]() ,即
,即
![]() 是
是
![]() 的中点。
的中点。
直线
![]() ,
,
![]() ,四边形
,四边形
![]() 是平行四边形,所以
是平行四边形,所以
![]() 过点
过点
![]() (与它们平行),
(与它们平行),
故它们的原像
![]() 共点或平行。
共点或平行。
例3 帕普斯(Pappus)定理
如图6所示,如果直线
![]() 分平面四边形
分平面四边形
![]() 为两个四边形
为两个四边形
![]() 和
和
![]() ,则三个四边形
,则三个四边形
![]() 、
、
![]() 、
、
![]() 的对角线的交点共线.
的对角线的交点共线.

证明 设
![]() 分别是四边形
分别是四边形
![]() 、
、
![]() 和
和
![]() 的对角线
的对角线
![]() 与
与
![]() 、
、
![]() 与
与
![]() 、
、
![]() 与
与
![]() 的交点,
的交点,
![]() 是直线
是直线
![]() 和
和
![]() 的交点,仿照例1,适当地选取中心射影,使得四边形
的交点,仿照例1,适当地选取中心射影,使得四边形
![]() 所在平面
所在平面
![]() 映射到平面
映射到平面
![]() ,并且在此中心射影下,
,并且在此中心射影下,
![]() 是平面
是平面
![]() 上的影消线。
上的影消线。
在此中心射影下,图6变为图7,
因为
![]() 与
与
![]() 交于无穷远点
交于无穷远点
![]() ,所以
,所以
![]() ,
,
因为
![]() 与
与
![]() 交于无穷远点
交于无穷远点
![]() ,所以
,所以
![]() 。
。
由
![]() 得
得
![]() ,
,
由
![]() 得
得
![]() ,
,
上式等号两端对应相乘得
![]() ,
,
由此得
![]() ,
,
故
![]() 交
交
![]() 于无穷远点
于无穷远点
![]() ,
,
这样
![]() 与
与
![]() 的交点
的交点
![]() 必在平面
必在平面
![]() 的影消线
的影消线
![]() 上。
上。
(当
![]() 与
与
![]() 平行时的情形,留给学员自己证)。
平行时的情形,留给学员自己证)。
帕普斯定理另外的叙述方式:直线
![]() 上在三个不同的点
上在三个不同的点
![]() 与另一直线
与另一直线
![]() 上三个不同的点
上三个不同的点
![]() ,设
,设
![]() 与
与
![]() 、
、
![]() 与
与
![]() 、
、
![]() 与
与
![]() 依次相交于点
依次相交于点
![]() ,则
,则
![]() 在一条直线
在一条直线
![]() 上。这条直线
上。这条直线
![]() 称为帕普斯线。
称为帕普斯线。
例4 代沙格(Desarques)定理及其逆定理
代沙格定理 两个三角形
![]() 与
与
![]() 位于同一平面上。若直线
位于同一平面上。若直线
![]() 共点,则三对直线
共点,则三对直线
![]() 与
与
![]() ,
,
![]() 与
与
![]() ,
,
![]() 与
与
![]() 的交点共线。
的交点共线。
逆定理 两个三角形
![]() 与
与
![]() 位于同一平面上。若三对直线
位于同一平面上。若三对直线
![]() 与
与
![]() ,
,
![]() 与
与
![]() ,
,
![]() 与
与
![]() 的交点共线,则直线
的交点共线,则直线
![]() 共点。
共点。
即平面上的两个对应三角形的对应边的交点共线当且仅当对应顶点的连线共点。

证明 首先证明代沙格定理:若两个三角形
![]() 与
与
![]() 的对应顶点的连线
的对应顶点的连线
![]() 共点于
共点于
![]() ,则对应边
,则对应边
![]() 与
与
![]() ,
,
![]() 与
与
![]() ,
,
![]() 与
与
![]() 的交点
的交点
![]() 共线。
共线。
选取适当的中心射影(射影中心记为
![]() ),将
),将
![]() 所在平面
所在平面
![]() 映射到平面
映射到平面
![]() 上,使得直线
上,使得直线
![]() 是平面
是平面
![]() 上的影消线。在此中心射影下,
上的影消线。在此中心射影下,
![]() 与
与
![]() 的像为
的像为
![]() 与
与
![]() 。
。
则
![]() (因为它们交于无穷远点
(因为它们交于无穷远点
![]() ),从而
),从而
![]() ;
;
![]() (因为它们交于无穷远点
(因为它们交于无穷远点
![]() ),从而
),从而
![]() 。
。
由上两式得
![]() ,
,
故
![]() ,从而
,从而
![]() 与
与
![]() 交于无穷远点
交于无穷远点
![]() ,
,
故
![]() 与
与
![]() 的交点
的交点
![]() 落在平面的影消线
落在平面的影消线
![]() 上,即
上,即
![]() 共线。
共线。
其次证明代沙格定理的逆定理 如果两个三角形
![]() 与
与
![]() 的对应边
的对应边
![]() 与
与
![]() ,
,
![]() 与
与
![]() ,
,
![]() 与
与
![]() 的交点
的交点
![]() 共线,则对应顶点的连线
共线,则对应顶点的连线
![]() 共点。
共点。
将三角形
![]() 与
与
![]() 所在平面
所在平面
![]() 中心射影到平面
中心射影到平面
![]() 上,使得点
上,使得点
![]() 所共的直线是平面
所共的直线是平面
![]() 上的影消线。在这一中心射影下,
上的影消线。在这一中心射影下,
![]() 与
与
![]() 变成对应边平行的相似三角形
变成对应边平行的相似三角形
![]() 与
与
![]() (如图9所示)
(如图9所示)
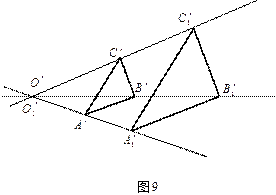
设
![]() 是
是
![]() 和
和
![]() 的交点,
的交点,
![]() 是
是
![]() 和
和
![]() 的交点,
的交点,
则有
![]() 。
。
又由
![]() ,
,
可得
![]() 。
。
因而有
![]() ,即
,即
![]() 与
与
![]() 重合。
重合。
由于直线
![]() 共点,故直线
共点,故直线
![]() 也共点。
也共点。
例5 巴斯卡(Pascal)定理
圆内接六边形的三对对边的交点共线。
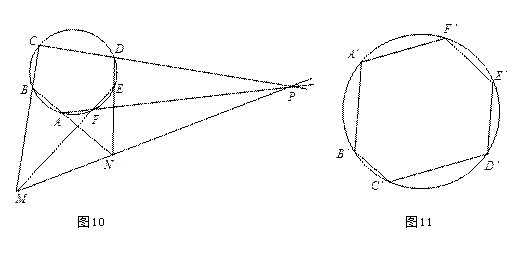
证明 设
![]() 是圆,
是圆,
![]() 是圆
是圆
![]() 的内接六边形。
的内接六边形。
![]() 分别是是六边形
分别是是六边形
![]() 三对对边
三对对边
![]() 、
、
![]() 、
、
![]() 的交点。
的交点。
由§2.2节球极平面射影性质2知,可取中心射影把圆所在的平面
![]() 映射到某一平面
映射到某一平面
![]() 上,使得
上,使得
![]() 变成
变成
![]() 上的一个圆
上的一个圆
![]() ,直线
,直线
![]() 是此中心射影下平面
是此中心射影下平面
![]() 上的影消线,
上的影消线,
此时有
![]() ,
,
从而
![]() ,
,
于是
![]() 。
。
观察
![]()
![]() ,
,
于是
![]() ,
,
即直线
![]() 与
与
![]() 相交于无穷远点
相交于无穷远点
![]() 。
。
所以六边形
![]() 的三对对边的交点
的三对对边的交点
![]() 落在
落在
![]() 上的无穷远直线上,
上的无穷远直线上,
故
![]() 共线。
共线。
