德国数学家克莱因（Klein）的几何学观点：几何学是研究图形在一个变换群的变换下保持不变的那些性质的一门学科。这一观点强调了有许多种几何而不是只有一种通常意义下的欧几里得几何，并且说明为了要得到一种几何学，只需要选择一个变换群就够了。

变换群的概念已成为近代数学中最重要的概念之一，这一节中我们将介绍最基本的知识。

一、点变换

定义1  图形 到其自身上点的一一对应 ，即双射 称为图形 到自身的点变换，简称为图形 （或空间 ）上的变换。

定义2  如果点变换 ，使图形 上的点有对应关系 ，则反过来也存在一一对应 ，称一一对应 为变换 的逆变换。

定义3  如果一一对应 ，使图形 上的每一点都对应自身，即对于任意 ，都有 ，称 为恒等变换。

设 都是图形 到自身的点变换。如果对 上的点有 ， ,则连续施行两次变换 后，得到一个变换的对应关系 ，它显然也是图形到自身的一一对应。

把这个新的变换记为 ，其对应关系为：

定义4  连续施行变换 和 所得的变换 称为变换 和 的乘积。

定义5  设 和 是图形 上的变换，如果对于任意 ，总有 ，则称两变换相等，记做 。

图形 上的变换具有如下性质：

性质1 

证明  设 ， ，

于是  ，

  ，

所以有  .

性质2 

证明  设 ，

于是  ，

  ，

所以有 .

性质3  ，即点变换满足结合律.

证明  对于任意 ，设 ，

则  ，

    ，

所以有 。

由性质3，可记 为 。

注意：一般情况下，点变换不满足交换律，即

二、点变换的例子

下面这几个例子，都是我们知道的、常见的变换。在这里只给出定义，然后用解析几何的方法探讨它们的坐标表达式或称变换式。这样就可以与解析几何联系起来，也便于同坐标变换进行比较。

例1  平面上的平移变换

定义  如果变换使平面上的每一点都沿同一方向移动相同的距离，即把平面上的任意一点 变到另一点 ，使得向量 总等于一个确定的向量 ，这种变换称为平移变换，简称平移。

取直角坐标系 ，及非零向量 ， 的坐标为 。设平面上任意点 ，按向量 平移到点 ，即 （图1），

则有

   

故平移变换 公式为：

例2  平面上绕一点 的旋转变换

定义  平面上绕它上面一点 的旋转变换，是使平面上任意一对对应点 和 与一个定点 连结的线段都相等，即 ，且有向角 等于确定的有向角 ，其中点 称为旋转中心，有向角 称为旋转角。

取直角坐标系 ，以原点 为旋转中心，旋转角为 ，平面上任意一点 旋转到 ，令 ，则 ，且

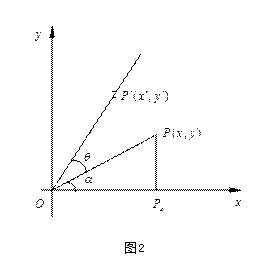
于是

     

     

     

     

同理

故旋转变换 公式为：

由上面方程组解出 和

得

即

这就是旋转变换 的逆变换 的公式，其旋转角为 。

例3  平面上的轴反射变换

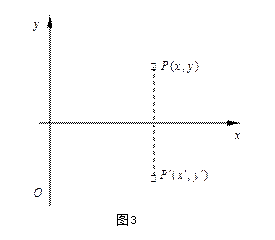
定义  如果平面上的变换，使每一对对应点 和 所连结的线段 ，都被一确定的直线 垂直平分，则这种变换称为轴反射变换，或直线反射变换，或关于直线的对称变换，直线 称为对称轴，点 和 称为对称点。

取反射轴为 轴建立直角坐标系 ，

平面上任意点 在轴反射变换下

的对应点为 ，

则轴反射变换 公式为：

例4  平面上的位似变换

定义  如果一个图形的点 和另一个图形上的点 分别对应，并且满足：（1）直线 都经过同一点 ；

（2） ，

那么这两个图形叫做位似图形， 叫做位似中心， 叫做位似系数或相似系数。

定义  从变换的角度来看，如果将位似图形 和 上的点之间的对应看成是平面到自身的点之间的一一对应，便成了一个变换，称为位似变换。

如果把等式（2）中的各线段的比看成是有向线段的比，当对应点在位似中心的两旁时， 与 反向，比值 ，这时称为反向位似变换，两个图形称为内位似；当对应点在位似中心的同侧时， 与 同向，比值 ，这时称为同向位似变换，两个图形称为外位似。

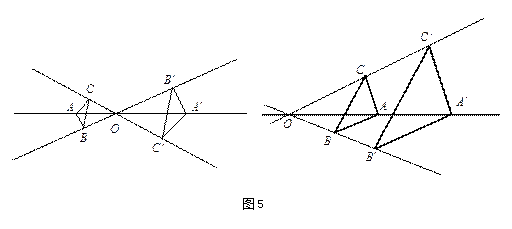
如果图形 经过一个位似变换，变成图形 ，则两个图形就是位似图形。

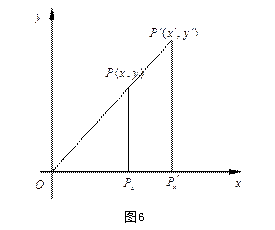
以坐标原点为位似中心建立直角坐标系 ，位似系数为 的位似变换，如果将任意点 变到 ，则有

故有

这就是以原点为位似中心的位似变换公式。

例5  平面上向着一条直线的伸缩变换

定义  给定一直线 ，对于平面上任意点 ，做 于点 ，使点 对应于射线 上一点 ，且 ，称这个对应为向着一条直线的伸缩变换， 称为伸缩系数。

当 时， ，即将 沿 压缩到 ，这种变换也称向着一直线的压缩变换；

当 时， 即将 沿 伸长到 ，这种变换称为向着一直线的伸长变换。

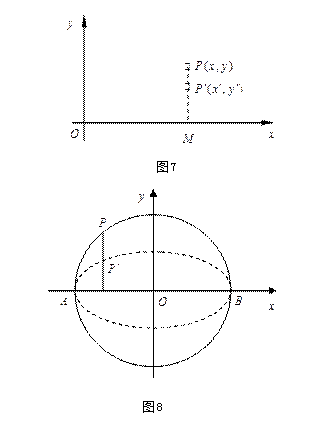
以定直线为 轴建立直角坐标系 ，伸缩系数为 的伸缩变换将平面上任意点 变成 ，则有

所以伸缩变换 公式为：

以定直线为 轴建立直角坐标系 ，

取压缩系数 的压缩变换，

将已知圆 变换成：

即

此方程对应的图形为椭圆。

三、变换群的基本知识

为了研究变换群，首先简要介绍代数中抽象群的概念

定义  如果对于集合 中任意一对有序元素 和 ，在二元运算 之下，总对应 中一个元素 ，称集合 在二元运算 之下是封闭的。

例如：整数集合，在二元运算加法 （或减法 ，或乘法 ）之下是封闭的，但其在二元运算除法 之下就不再是封闭的。

例如：如果集合 是平面上全部点的集合，二元运算是“取中点”，则 在此二元运算下是封闭的。

定义  如果集合 及其上二元运算 满足

（1） 在运算 之下是封闭的，即 ，则 ；

（2）对 中任意三个元素 ，关于运算 满足结合律： ；

（3） 中存在一个元素 ，对 中的任意元素 有 (元素 称为 的单位元或恒等元）；

（4）对于 中的每个元素 ，在 中存在元素 ，使得 (元素 称为元素 的逆元），

则称 构成一个群。

例如：1）整数集合在加法运算之下构成群，其单位元是 ，元素 的逆元为 ；

2）整数集合在乘法运算之下不构成群，因为元素 的逆元 不一定是整数。

定义  如果群 的二元运算 满足交换律 ，称 为交换群（或Abel群）。   

      如果群 的子集 在群 的同样运算下也构成群 ，称 为群 的子群。

定义  设由点变换构成的集合 ，满足下列两个条件：

（1） 中任意两个变换的乘积仍是 中的变换，即具有封闭性；

（2） 中的每个变换都有逆变换，而且逆变换也是 中的一个变换，

称 为变换群。

变换群的定义，与抽象群的定义是一致的。因为变换群中，集合 的元素是点变换。由点变换的性质知，抽象群定义中条件（2）、（3）在变换群定义中可省去。

定义  如果图形 在变换 下还变成自身，称 为变换 的不动图形或二重图形。

例如：平面上以直线 为轴的反射变换，在此变换下，

上的每个点都是不动点，故轴反射变换把直线 变成直线 ，它是一条不动直线，称为点态的不动直线；

另外，垂直于 的每条直线，也是不动直线，称为线态的不动直线。

定义  平面上的图形在一变换群 的所有变换下都保持不变的性质和量，称为变换群 下的不变性质和不变量，统称为变换群 下的不变性。