第二章 几何变换与变换群
 知识点六:几个重要的变换群
知识点六:几个重要的变换群
下面讨论正交变换(运动)、相似变换、仿射变换、射影变换,以及它们的基本性质。这些变换生成的变换群群可以决定四种不同的几何学,即欧氏几何学、相似几何学、仿射几何学和射影几何学。
一、正交变换群
定义 平面上保持两点间距离不变的点变换称为正交变换或运动,即建立平面上所有点的集合与它自身的一一对应,且对于平面上任意两点
![]() ,若其对应点分别为
,若其对应点分别为
![]() ,则对应线段的长度
,则对应线段的长度
![]() 。
。
正交变换具有以下基本不变的性质:
性质1 正交变换把直线变成直线,并且保持点和直线的结合关系和共线三点的介于关系。
证明 设
![]() 是直线 上有序的三点,它们共线的充要条件为
是直线 上有序的三点,它们共线的充要条件为
![]()
如果正交变换把它们依次变为
![]() ,则有:
,则有:
![]() ,
,
于是
![]() ,
,
故
![]() 在同一直线上。
在同一直线上。
就是说,正交变换把共线点变成共线点,直线变成直线。
性质2 正交变换把不共线的点变成不共线的点
证明 设
![]() 为不共线三点,则三点不共线充要条件为
为不共线三点,则三点不共线充要条件为
![]()
如果它们在正交变换下依次变为
![]() ,则有:
,则有:
![]() ,
,
于是
![]() ,
,
故
![]() 不共线。
不共线。
由性质1、2知,正交变换把相交直线变成相交直线,把角变成角。
性质3 正交变换把平行直线变成平行直线。
证明 设直线
![]() ,在正交变换下它们的对应直线分别为
,在正交变换下它们的对应直线分别为
![]() 。
。
假设
![]() 相交于
相交于
![]() ,由性质1,
,由性质1,
![]() 的原像
的原像
![]() 点必既在
点必既在
![]() 上,又在
上,又在
![]() 上,从而与
上,从而与
![]() 矛盾。
矛盾。
性质4 正交变换保持角的大小不变。
证明 已知
![]() ,其中
,其中
![]() 为角的两边上任意取定的两点,设正交变换把
为角的两边上任意取定的两点,设正交变换把
![]() 变成
变成
![]() ,
,
则
![]() ,
,
于是
![]() ,故
,故
![]() 。
。
定理 平面上的正交变换由不共线的三对对应点惟一决定。
证明 设不共线三点
![]() 在正交变换下的对应点分别为
在正交变换下的对应点分别为
![]() 。
。
在平面上取一点
![]() ,连
,连
![]() 交线段
交线段
![]() 于点
于点
![]() ,则由
,则由
![]() ,点
,点
![]() 在线段
在线段
![]() 被惟一确定,又由
被惟一确定,又由
![]() ,且由性质1,点
,且由性质1,点
![]() 的对应点
的对应点
![]() 被惟一确定
被惟一确定
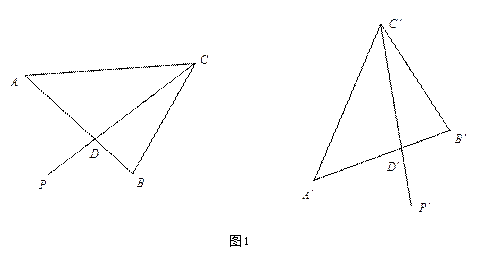
正交变换可分成两类:
定义 把一个
![]() 变成与它同向的合同
变成与它同向的合同
![]() ,即点
,即点
![]() 和点
和点
![]() 有同一旋转方向,称这类正交变换为第一种正交变换或刚体运动。
有同一旋转方向,称这类正交变换为第一种正交变换或刚体运动。
第一种正交变换的一般情形,总可以通过旋转与平移两种变换乘积来实现。
第一种正交变换的坐标表示式:
取直角坐标系
![]() ,设以坐标原点为中心,
,设以坐标原点为中心,
![]() 为旋转角的旋转变换为
为旋转角的旋转变换为
![]() ,
,
![]() 将平面上点
将平面上点
![]() 变成点
变成点
![]() ,
,
则旋转公式为
![]() 。
。
设点
![]() 的坐标为
的坐标为
![]() ,按有向线段
,按有向线段
![]() 的方向,距离为
的方向,距离为
![]() 进行平移得变换
进行平移得变换
![]() ,
,
![]() 将
将
![]() 变成点
变成点
![]() ,
,
则平移公式为
![]() 。
。
于是第一种正交变换公式为:
![]()
定义 把一个
![]() 变成合同
变成合同
![]() ,但两个三角形方向相反,称这类正交变换为第二种正交变换或称非刚体运动。
,但两个三角形方向相反,称这类正交变换为第二种正交变换或称非刚体运动。
第二种正交变换可以是轴反射,或轴反射与刚体运动的乘积。
设以
![]() 轴为对称轴的反射,将平面上的任意点
轴为对称轴的反射,将平面上的任意点
![]() 变成
变成
![]() ,刚体运动又将
,刚体运动又将
![]() 变成
变成
![]() ,
,
则有
![]() ,
,
![]() ,
,
于是第二种正交变换为:
![]() 。
。
两种正交变换公式可以统一写成:
![]()
当
![]() 时为第一种正交变换,包括平移(
时为第一种正交变换,包括平移(
![]() ),旋转(
),旋转(
![]() );
);
当
![]() 时为第二种正交变换,包括轴反射(
时为第二种正交变换,包括轴反射(
![]() ,
,
![]() )。
)。
正交变换也常写成:
![]()
且满足正交条件
![]() ,且系数行列式为
,且系数行列式为
![]() 。
。
当
![]() 时为第一种正交变换;当
时为第一种正交变换;当
![]() 时为第二种正交变换。
时为第二种正交变换。
定理 平面上全体正交变换的集合是一个群
证明
(1)两个正交变换的乘积是正交变换
设正交变换
![]() 将平面上任意两点
将平面上任意两点
![]() 变成
变成
![]() ,正交变换
,正交变换
![]() 又将
又将
![]() 变成
变成
![]() ,
,
因为乘积
![]() 保持平面上点间的一一对应,所以
保持平面上点间的一一对应,所以
![]() 将两点
将两点
![]() 变成
变成
![]() ,
,
又由
![]() ,
,
得
![]() 故两个正交变换的乘积是正交变换。
故两个正交变换的乘积是正交变换。
(2)设正交变换
![]() 将点
将点
![]() 变成
变成
![]() ,且
,且
![]() ;其逆变换
;其逆变换
![]() ,使
,使
![]() ,对应
,对应
![]() ,且
,且
![]() ,所以
,所以
![]() 是一个正交变换。
是一个正交变换。
由(1)、(2)知,平面上全部正交变换的集合
![]() 是一个群,称为正交群或运动群。
是一个群,称为正交群或运动群。
二、平面上的相似变换群
定义 如果平面上的点变换,使任意一对对应线段
![]() 和
和
![]() ,总有
,总有
![]() ,
,
![]() 为确定的正的常数,称这个变换为相似变换,
为确定的正的常数,称这个变换为相似变换,
![]() 称为相似比或相似系数。
称为相似比或相似系数。
在相似变换下,如果图形
![]() 变成图形
变成图形
![]() ,称图形
,称图形
![]() 相似于图形
相似于图形
![]() ,记作
,记作
![]()
相似变换有以下基本不变性质:
性质1 把直线变成直线,且保持点和直线 的结合关系和共线三点的介于关系
证明 设
![]() 是直线
是直线
![]() 上的三个点,且点
上的三个点,且点
![]() 介于
介于
![]() 之间,
之间,
在相似变换下它们的对应点分别为
![]() ,
,
据定义则有
![]() ,
,
由此得
![]() ,
,
由于
![]() ,故
,故
![]() ,
,
所以
![]() 也在一直线上,且
也在一直线上,且
![]() 介于
介于
![]() 之间。
之间。
依据性质1,得到:
性质2 相似变换把不共线点变成不共线点。
由性质1、2,两相交直线变为相交直线,射线变为射线,角变为角。
性质3 相似变换把平行直线 变成平行直线。
证明 已知直线
![]() ,在相似变换下,它们的对应直线分别为
,在相似变换下,它们的对应直线分别为
![]() 和
和
![]() ,
,
假设
![]() 和
和
![]() 相交于点
相交于点
![]() ,据性质1,点
,据性质1,点
![]() 的原像
的原像
![]() 必既在直线
必既在直线
![]() 上,又在直线
上,又在直线
![]() 上。
上。
故
![]() 和
和
![]() 有公共点
有公共点
![]() 。
。
与已知矛盾。
定义 一条直线上三个点
![]() ,则点
,则点
![]() 与
与
![]() 构成的两个有向线段的比
构成的两个有向线段的比
![]() 称为这三点的单比,记作
称为这三点的单比,记作
![]() 。
。
![]() 称为基础点,
称为基础点,
![]() 称为分点。
称为分点。
如果
![]() 在线段
在线段
![]() 上,点
上,点
![]() 称为内分点,则
称为内分点,则
![]() ;
;
若
![]() 不在线段
不在线段
![]() 上,点
上,点
![]() 称为外分点,则
称为外分点,则
![]() 。
。
实际上单比
![]() 和中学几何线段
和中学几何线段
![]() 的分比
的分比
![]() ,(
,(
![]() 为分点),只差一个负号,
为分点),只差一个负号,
即
![]() 。
。
性质4 相似变换保持共线三点的单比不变。
证明 设共线三点
![]() ,在相似变换下变成三点
,在相似变换下变成三点
![]() ,
,
则有
![]() ,
,
由此得
![]() ,即
,即
![]() 。
。
性质5相似变换保持角的大小不变。
证明 对于任意
![]() ,
,
![]() 分别为两条边上的已知点,
分别为两条边上的已知点,
在相似变换下
![]() 变成
变成
![]() ,
,
![]() 对应点分别为
对应点分别为
![]() ,且
,且
![]() ,
,
因此
![]() ,故
,故
![]() 。
。
据上面基本性质,可推出:
定理3 相似变换由不共线的三对对应点惟一确定。
定义 把一个三角形变为同向三角形的相似变换称为第一种或同向相似变换;把一个三角形变为不同向三角形的相似变换,称为第二种或反向相似变换。
当相似变换的相似比
![]() 时,
时,
![]() 这时的相似变换就是正交变换,所以正交变换是相似变换的特殊情形。
这时的相似变换就是正交变换,所以正交变换是相似变换的特殊情形。
当对应点的连线都经过同一个确定点
![]() 时,相似变换就是位似变换,所以位似变换是相似变换的特殊情形。外位似变换的位似比等于相似变换的相似比
时,相似变换就是位似变换,所以位似变换是相似变换的特殊情形。外位似变换的位似比等于相似变换的相似比
![]() ,内位似变换的位似比等于
,内位似变换的位似比等于
![]() 。
。
定理 相似变换是位似变换与正交变换的乘积
证明:设相似变换
![]() (相似系数为
(相似系数为
![]() )将
)将
![]() 变成
变成
![]() ,
,
则
![]() 。
。
任取一点
![]() 为位似中心,
为位似中心,
![]() 为位似系数,经位似变换
为位似系数,经位似变换
![]() 将
将
![]() 变成
变成
![]()
则
![]() ,且
,且
![]() 。
。
经过一次运动
![]() ,将
,将
![]() 变成
变成
![]() ,
,
则变换积
![]() 将
将
![]() 变成
变成
![]() ,即
,即
![]() 。
。
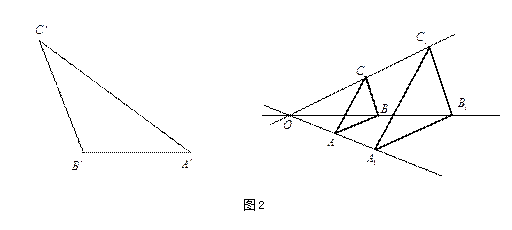
相似变换的坐标表示式:
取直角坐标系
![]() ,以坐标原点
,以坐标原点
![]() 为位似中心,以
为位似中心,以
![]() 为位似比的位似变换
为位似比的位似变换
![]() ,将平面上任意一点
,将平面上任意一点
![]() 变成
变成
![]() ,则
,则
![]() ,
,
再进行运动,将
![]() 变成
变成
![]() ,则
,则
![]() ,
,
这两个变换的积为
![]() ,
,
或写成
![]() ,
,
满足条件
![]() ,且系数行列式
,且系数行列式
![]() 。
。
当
![]() 时为第一种相似变换,当
时为第一种相似变换,当
![]() 时为第一种相似变换.
时为第一种相似变换.
定理 平面上全部相似变换构成的集合是一个群。
三、平面上的仿射变换群
定义 如果平面上的一个点变换,把共线的任意三点变成共线的三点,并且保持三点的单比不变,称这个点变换为仿射变换。
显然,正交变换和相似变换都是仿射变换的特殊情形。
仿射变换有以下基本不变的性质:
性质1 仿射变换把直线变成直线,并且保持共线三点的介于关系。
证明 由仿射变换的定义,设
![]() 为直线
为直线
![]() 上任意三点,则其对应点
上任意三点,则其对应点
![]() 也为共线三点,故仿射变换把直线变成直线。
也为共线三点,故仿射变换把直线变成直线。
若
![]() 介于
介于
![]() 之间,则
之间,则
![]() ,而
,而
![]() ,
,
故
![]() ,即
,即
![]() 位于
位于
![]() 之间。
之间。
性质2 仿射变换把不共线三点变成不共线三点。
证明 设不共线三点
![]() ,在仿射变换
,在仿射变换
![]() 下分别对应
下分别对应
![]() 点
点
假设
![]() 在同一直线
在同一直线
![]() 上,设
上,设
![]() 是平面上不与
是平面上不与
![]() 重合的任一点,过
重合的任一点,过
![]() 做一直线
做一直线
![]() ,
,
![]() 分别与直线
分别与直线
![]() 和
和
![]() 交于
交于
![]() 两点(如图所示)。
两点(如图所示)。
在变换
![]() 下,点
下,点
![]() 分别对应于
分别对应于
![]()
因为
![]() 共线,所以
共线,所以
![]() 也共线,则
也共线,则
![]() 在直线
在直线
![]() 上,
上,
同理
![]() 也在
也在
![]() 上;
上;
又
![]() 共线,所以
共线,所以
![]() 在
在
![]() 上。
上。
于是整个平面上的点都映到直线
![]() 上,这破坏了点变换的一一对应关系。
上,这破坏了点变换的一一对应关系。
故
![]() 不共线。
不共线。
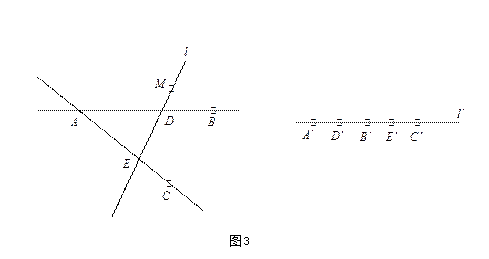
由性质1、2知,在仿射变换下相交直线仍变成相交直线,角变成角。
性质3 仿射变换把平行直线变成平行直线。
证明 设直线
![]() ,仿射变换
,仿射变换
![]() 将它们分别变为直线
将它们分别变为直线
![]() 。
。
若
![]() 与
与
![]() 相交于
相交于
![]() ,则
,则
![]() 的原像既在
的原像既在
![]() 上又在
上又在
![]() 上,产生矛盾,
上,产生矛盾,
故
![]() 。
。
性质4 在仿射变换下平行线段的比不变。
证明 设线段
![]() 平行于线段
平行于线段
![]() ,经仿射变换
,经仿射变换
![]() 后,其对应线段
后,其对应线段
![]() 和
和
![]() 也平行。
也平行。
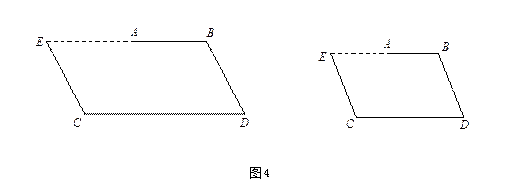
做
![]() ,与直线
,与直线
![]() 交于点
交于点
![]() ,则
,则
![]() 点的对应点
点的对应点
![]() 在直线
在直线
![]() 上,且
上,且
![]() ,因四边形
,因四边形
![]() 与
与
![]() 都是平行四边形,所以
都是平行四边形,所以
![]() ,
,
![]() 。由仿射变换
。由仿射变换
![]() 保持共线三点的单比,故
保持共线三点的单比,故
![]()
即
![]() ,所以
,所以
![]() 。
。
定理 不共线的三对对应点决定惟一的一个仿射变换。
(证法同正交变换中类似的定理,只需将距离换成共线三点的单比。)
在仿射变换下,图形的不变性质和不变量统称仿射性质,是仿射几何研究的对象和内容。
定理 平面上所有的仿射变换的集合是一个群
证明 (1)设
![]() 和
和
![]() 是任意两个仿射变换,且
是任意两个仿射变换,且
![]() 。
。
事实上,设
![]() 共线,则
共线,则
![]() 共线,
共线,
![]() 共线,
共线,
且
![]()
(2)设
![]() 是任意一个仿射变换。
是任意一个仿射变换。
将共线三点
![]() 变成
变成
![]() ,且
,且
![]()
则
![]() 把共线三点
把共线三点
![]() 变成
变成
![]() ,且
,且
![]()
于是
![]() 仍是仿射变换。
仍是仿射变换。
综上所证,平面上全体仿射变换的集合是一个群。
这个群称为仿射变换群,或仿射群。
它包含相似变换群,也包含正交变换群;正交变换群是前两者的子群。
四、平面上的射影变换群
本章开始讲了中心射影,为了使直线到直线的中心射影成为点的一一对应,在两条直线上各增加一个新点,称为无穷远点,并把成一一对应的中心射影称为直线
![]() 与直线
与直线
![]() 间的透视对应;为了使从平面
间的透视对应;为了使从平面
![]() 到
到
![]() 平面的中心射影是一一对应,在两个平面上各添加一条由无穷远点构成的无穷远直线。当把平面上的无穷远直线与通常意义下的直线不加区别地等同看待时,这样的平面称为射影平面,其上的直线称为射影直线。
平面的中心射影是一一对应,在两个平面上各添加一条由无穷远点构成的无穷远直线。当把平面上的无穷远直线与通常意义下的直线不加区别地等同看待时,这样的平面称为射影平面,其上的直线称为射影直线。
从平面
![]() 到平面
到平面
![]() ,再从平面
,再从平面
![]() 到平面
到平面
![]() ,再从平面
,再从平面
![]() 到平面
到平面
![]() ,经过有限次透视对应的乘积,可使平面
,经过有限次透视对应的乘积,可使平面
![]() 上的点和平面
上的点和平面
![]() 上的点建立一一对应的关系。称为平面
上的点建立一一对应的关系。称为平面
![]() 和平面
和平面
![]() 间的射影对应。
间的射影对应。
如果
![]() 与
与
![]() 是同一个平面,则此时构成平面到自身的一一对应,称为射影变换。
是同一个平面,则此时构成平面到自身的一一对应,称为射影变换。
定义 设
![]() 为平面上的四个共线点,称两个单比
为平面上的四个共线点,称两个单比
![]() 和
和
![]() 的比为这四点的交比或复比,记作
的比为这四点的交比或复比,记作
![]() ,其中
,其中
![]() 和
和
![]() 称为基础点对,
称为基础点对,
![]() 和
和
![]() 称为分点对。
称为分点对。
![]()
定义 如果四点
![]() 的交比
的交比
![]() ,则称点对
,则称点对
![]() 和
和
![]() 调和分离点对
调和分离点对
![]() 和
和
![]() ,或称点对
,或称点对
![]() 与点对
与点对
![]() 调和共轭,这时也称
调和共轭,这时也称
![]() 为
为
![]() 的第四调和点,交比值
的第四调和点,交比值
![]() 称为调和比。
称为调和比。
定理 中心射影保持共线四点的交比不变。
证明 如图
![]() 为射影中心,从直线
为射影中心,从直线
![]() 到直线
到直线
![]()
的中心射影
直线
![]() 上任意四点
上任意四点
![]() 在中心射影下的像分别是直线
在中心射影下的像分别是直线
![]() 上的
上的
![]() 。
。

设
![]() 的
的
![]() 边上的高长度为
边上的高长度为
![]() ,
,
![]() 的
的
![]() 边上的高长度为
边上的高长度为
![]() ,
,
则
![]() ,
,
于是
![]() ,
,
同理
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
于是
![]()
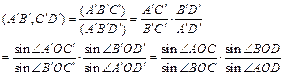
故
![]() 。
。
定义 如果平面上的点变换使共线三点还变成共线三点,并且保持共线四点的交比不变,称此变换为平面上的射影变换。
因为正交变换、相似变换、仿射变换都保持共线三点的单比不变,必然保持共线四点的交比不变,所以这些变换都是射影变换。
射影变换有以下基本不变性质:
性质1 直线变为直线并保持点线的结合关系。
性质2 把不共线点变为不共线点。
故射影变换把共线点变成共线点,把共点线变成共点线,把
![]() 边形变成
边形变成
![]() 边形等等。
边形等等。
射影变换下的不变性质和不变量统称为射影性质。
定理 平面上全部射影变换的集合构成群。
证明 (1)设
![]() 是平面上的两个射影变换,
是平面上的两个射影变换,
![]() 是共线四点,
是共线四点,
据定义有
![]() ,且
,且
![]() ;
;
![]() ,且
,且
![]() ,
,
所以
![]() 仍是射影变换。
仍是射影变换。
(2)设
![]() 是平面的上射影变换,且
是平面的上射影变换,且
![]() 。
。
![]() ,且
,且
![]() ,
,
所以
![]() 是射影变换。
是射影变换。
故平面上全部射影变换的集合构成群
称之为射影变换群,仿射变换群、相似变换群、正交变换群都是它的子群。
