我们知道，位移、力、速度与加速度等都是矢量，而时间、质量等都是数量，这些矢量与数量间常常会发生某些结合的关系，如我们熟知的公式

                 ,

这里 表示力， 表示加速度， 表示质量。再如公式

                 ,

这里 表示位移, 表示速度， 表示时间。

在矢量的加法中，我们也已看到， 个矢量相加仍然是矢量，特别是 个相同的非零矢量 相加的情形，显然这时的和矢量的模为 的 n 倍， 方向与 相同。 个 相加的和常记做 或  。

定义1   实数 与矢量 的乘积是一个矢量，记做 ，它的模是 ； 的方向，当 时与 相同，当 时与 相反。我们把这种运算称为数量与矢量的乘法，简称为数乘。

      从这个定义我们立刻知道，当 或 时， , 所以 ，这时就不必讨论它的方向了， 当 时， 就是 的反矢量，因此我们常常把 简写做 。

  已知矢量 和它的单位矢量 ，下面的等式显然成立：

             ，或 。            ( 1.3−1 )

  由此可知，一个非零矢量乘以它的模的倒数，结果是一个与它同方向的单位矢量。

定理1  数量与矢量的乘法满足下面的运算规律：

1 )               ；              ( 1.3−2 )

2 )    结合律         ；      ( 1.3−3 )

3 )    第一分配律    ；   ( 1.3−4 )

4 )    第二分配律    。    ( 1.3−5 ) ，这里 为矢量， 为任意实数。

 

   证   1 )  根据定义1， ( 1.3−2 ) 显然成立。

     2 )  证明结合律 成立。

   当 或 中至少有一为0时，( 1.3−3 ) 显然成立。当 ， 时，矢量 与 的模都等于 ，从而它们的模相等；而它们的方向，当 与 同号时，都与 的方向一致；当 与 异号时，都与 的方向相反，因此矢量 与 的方向相同，

    所以有                 。             

  3)  证明第一分配律 成立。

    如果 ，或 及 中至少有一个为 ，那么等式 显然成立。

 SHAPE  \* MERGEFORMAT

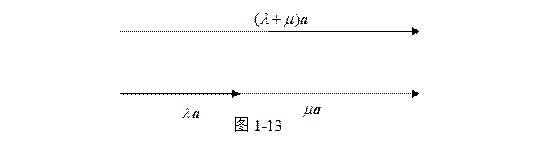
因此我们只须证明当 的情形。

     ( i ) 如果 （图1－13），这时显然 与 同向，  也同向，且

         ,

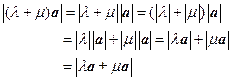所以     。

  ( ii )  如果 ，不失一般性，可设 ，再区分 和 两种情形。 下面只证前一种情形，后一种情形可相仿证明。

    假设 ， ， 。这时有 ， 根据(i)有

          ,

    所以                .

   4) 证明第二分配律 成立。

    如果 或 之中有一个为 ，等式显然成立，因此，这里只须对  

  的情形进行证明。

      ( i )  如果 共线，当 同向时，取 ；当 反向时，取 ，这样显然有 , 因此根据(1.3-3)与(1.3-4)有

             

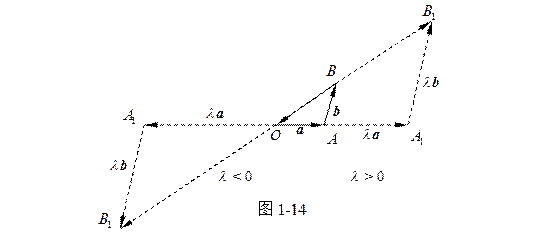
    ( ii )  如果 不共线，那么如图1−14 所示，显然由 为两边构成的 与由 为两边构成的 相似，因此对应的第三边所成矢量满足

                      ,

但                 ,

所以                 .

   从矢量的加法与数乘矢量的运算规律知，对于矢量也可以象实数及多项式那样去运算，例如

              .

   例1   设 是 的中线，求证 .

   证   如图1－15所示，

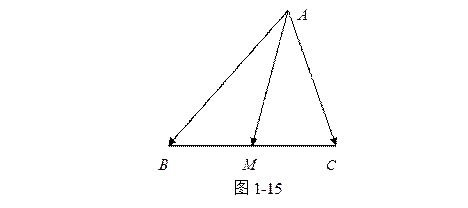
有           ,

所以          ,

但            ,

因而            ,

即               .

 

   例2   用矢量法证明“连结三角形两边中点的线段平行于第三边且等于第三边的一半”。

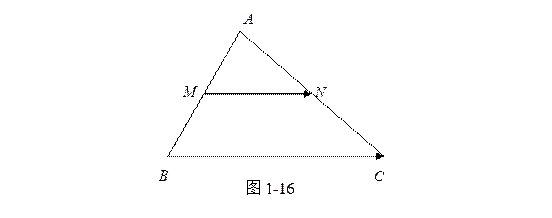
   证  设 的边 之中点分别为 （图1－16），那么

             

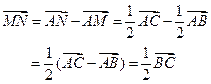
所以 ,且 。

  由此例可见，用矢量运算可以比较简洁地证明一些几何命题。