在研究两个矢量的数量积的基础上，现在我们来研究三个矢量的乘积。

如果我们先把矢量 作出数量积，然后再和第三个矢量 相乘，那么得到与矢量 共线的矢量，因此这样相乘的情况，不必再讨论。

     如果我们先把矢量 和 作出矢量积 ，那么这个矢量还可以与第三个矢量 再作数量积或矢量积，在前一种情形，我们得到 ，在后一种情形，我们得到 。在这一节我们先计论 的性质。

定义1  给定空间的三个矢量 ，如果先做前两个矢量 与 的矢量积，再做所得的矢量与第三个矢量 的数量积，最后得到的这个数称为三矢量 的混合积，记作 或 或 。

混合积具有下列性质：

定理1  三个不共面矢量 的混合积的绝对值等于以 为棱的平行六面体的体积 ，并且当 构成右手系时混合积是正数；当 构成左手系时，混合积是负数，也就是有 ，当 是右手系时 ；当 是左手系时 。

证  由于 三矢量不共面，把它们归结到共同的始点 可以构成以 为棱的平行六面体（图1-43），它的底面是以 为边的平行四边形，面积为 ，它的高 ，它的体积为 。

根据数量积定义 ,                   (1)

其中 是 和 的夹角。

当 成右手系时， ，因而由（1）得

。

当 成左手系时，

因而由(1)得

定理2  三矢量 共面的充要条件是 。

证  当 与 共线，即 时，或 时，显然 共面且又有 。下面假设 与 不共线，且 ，我们来证明定理也成立。

如果 ，即 ，则 ，另一方面据矢量积的定义知 ，所以三矢量 共面。

反过来，如果 共面，那么据 知 ，于是 ，即 。

定理3  轮换混合积的三个因子，并不改变它的值，对调任何两个因子要改变乘积的符号，即

         (1.9-2)

证  当 共面时，定理显然成立；当 不共面时，轮换因子或对调因子，混合积的绝对值都等于以 为棱平行六面体的体积（定理1）。又因为轮换 的顺序时，决不会把右手系变为左手系，也不会把左手系变为右手系，因而混合积不变，而当对调任意两个因子的位置时，就将右手系变成左手系，或将左手系变成右手系，所以这时混合积要改变符号。

推论1                            (1.9.3)

证 

例1  设三矢量 满足 ，试证三矢量 共面。

证 将 两边与 作数量积

得

而

所以 ，因而 共面。

下面在右手直角坐标系 下，我们用矢量的分量表示三个矢量的混合积。

定理4  若 ，那么

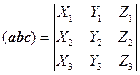             (1.9-4)

证  因为 ，

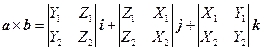根据数量积的分量表示法，得

，

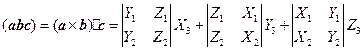所以(1.9-4)成立

根据定理2，从(1.9-4)式，立即可得：

三个矢量 ，共面的充要条件是 

        。

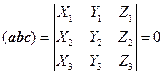例2  已知四面体 的顶点坐标 ，求它的体积。

解  四面体 的体积 等于以 和 为棱的平行六面体积的六分之一，因此；  

            

而 ，

所以 ，

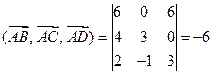从而

例3 设 为三个不共面的矢量，求矢量 对于 的分解式。

解  因为 不共面，所以 ，

为了要决定 的值，可在等式两边分别与矢量 作数量积，即在等式两边分别与 作混合积，那么有

而 ，

所以 ，

因为 不共面，所以 ，因此 ，

同理可求得 与 的值为 。

如果取直角坐标系，并设 的分量分别为

将这些分量代入上面的 对 的分解式与 的表达式，那么容易看出，上面的解法就是解线性方程组

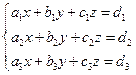
的克莱姆（Cramer）法则。