知识点十:三矢量的双重矢量积
定义1 给定空间三矢量,先作其中两个矢量的矢量积,再作所得矢量与第三个矢的矢量积,那么最后的结果仍然是一矢量,称为所给三矢量的双重矢量积简称为三矢矢积。
例如
![]() 就是三矢量
就是三矢量
![]() 的一个双重矢量积。
的一个双重矢量积。
首先我们可以明确
![]() 是和
是和
![]() 共面且垂直于
共面且垂直于
![]() 的矢量,这是因为根据矢量积的定义,立即知道
的矢量,这是因为根据矢量积的定义,立即知道
![]() 与矢量
与矢量
![]() 垂直,并且它与
垂直,并且它与
![]() 垂直,而
垂直,而
![]() 也与
也与
![]() 垂直,所以
垂直,所以
![]() 和
和
![]() 共面
共面
双重矢量积上述几何关系可以概括为下面一个定理:
定理 1
![]() (1.10-1)
(1.10-1)
证 如果
![]() 中有一个为零矢量,或
中有一个为零矢量,或
![]() 与
与
![]() 共线,或
共线,或
![]() 与
与
![]() 都垂直,那么(1.10-1)两边都为零矢量,定理显然成立。
都垂直,那么(1.10-1)两边都为零矢量,定理显然成立。
现在设
![]() 为三个非零矢量,且
为三个非零矢量,且
![]() 与
与
![]() 不共线,为了证明这时(1.10-1)也成立,我们先证明(1.10-1)中当
不共线,为了证明这时(1.10-1)也成立,我们先证明(1.10-1)中当
![]() 时成立,即有
时成立,即有
![]() (1 )
(1 )
由于
![]() 共面,而
共面,而
![]() 与
与
![]() 不共线,从而可设
不共线,从而可设
![]() (2 )
(2 )
(2)式两边先后与
![]() 作数量积得
作数量积得
![]() ,
(3)
,
(3)
![]() 。
(4)
。
(4)
利用公式(1.8-7)由(3)、(4)解得
![]() ,
(5)
,
(5)
(5)代入(2)即得(1)。
下面证(1.10-1)成立,因为三矢量
![]() 不共面,所以对于空间的任意矢量
不共面,所以对于空间的任意矢量
![]() ,根据(1.4-3)总有
,根据(1.4-3)总有
![]() ,
(6)
,
(6)
从而有
![]() ,
,
利用(1)式可得
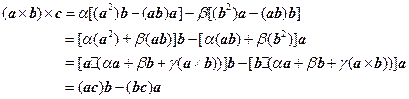 。
。
即(
必须指出,在一般情况下
![]()
这是因为
![]()
而
![]() 。
(1.10-2)
。
(1.10-2)
比较公式(1.10-1)和(1.10-2)可知,
![]() 和
和
![]() 在一般情况下是两个不同的矢量,因此双重矢量积不满足结合律。
在一般情况下是两个不同的矢量,因此双重矢量积不满足结合律。
利用公式(1.10-1)可以证明拉格朗日(Lagrange)恒等式
![]() 。
(1.10-3)
。
(1.10-3)
这是因为由公式(1.9-3),(1.10-1)得
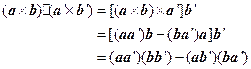
这就是(1.10-3)。
拉格朗日恒等式的一个特殊情况是
![]() 。
。
这就是(1.8-7)。
例1 试证
![]() 。
。
证 因为
![]() ,
,
![]() ,
,
![]()
三式相加得
![]() 。
。
例2 证明
![]()
证 设
![]() ,于是
,于是
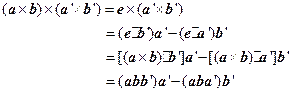 。
。
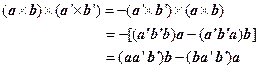 。
。
