在用向量法解几何问题时，要注意以下几个问题：

1．向量始点的选择

2．向量等式的运用

3．向量的线性关系

 

例1．求证连接平行四边形的一个顶点至对边中点的直线三等分对角线

                                       

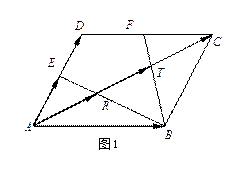
分析：设 为任意一个平行四边形， 、 分别为 及 的中点, 往证 三等分 。

证明  设 的交点分别为 ，

设 ，

则

（目标：证明 ）

由于向量 与 共线

故 （ 待定系数）    = 1 \* GB3 ①

由于 ，故 （ 待定系数）

而 ，故 ，

在 中，  

即               = 2 \* GB3 ②

由等式 = 1 \* GB3 ①与 = 2 \* GB3 ②得

即

由于 线性无关，

所以

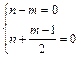
解得

代入 = 1 \* GB3 ①式得

同理可证 即

例2．证明以任意三角形的三中线为边可做一个三角形。

证明：设 为任意三角形， 分别为各边中点

设 ， ，

则

设 ， ，

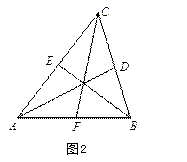
往证                      

在 中

在 中

在 中

于是

故命题得证

 

例3．试证 的三条中线 相交于一点 。

    证明：在 所在平面外任取一点 为坐标原点，

设 ， ，

则 ，

同理 ，

 

若 为直线 上的任一点且

由于三向量 终点在同一直线 上

故可设

            eq \o\ac(○,1)1

同理若 为 上的任一点，且 ，

则            eq \o\ac(○,2)2

若 为 上的任一点，且 ，

则            eq \o\ac(○,3)3

因此如果 是 和 的公共点，

则由 eq \o\ac(○,1)1和 eq \o\ac(○,2)2可得

由于 都是非零向量，且 不在同一平面上，

故

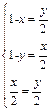
解得

同理由 eq \o\ac(○,1)1和 eq \o\ac(○,3)3和可得

从而

故命题得证。

例4.证明引自同一始点的空间四个向量的终点位于同一平面上的充要条件是它们满足系数之和为0的向量方程。

   

证明：设 为空间中有相同的始点O的四个向量，

设 ， ， ，

首先设终点 在同一平面上

故 共面，从而满足向量方程

而 ， ，

故

上式系数之和为

反之，设始点相同的四个向量满足方程 ，且 ，其中 不全为零

    不妨设 ，则有

于是有

即

这说明 三个向量共面，

即向量 共面，故 四点共面。

 

例5．用向量法证明梅内劳斯定理：

        设 为任意三角形， 为其内任一点，连接 并延长使之

分别交对边于

求证：

证明：取 所在平面外任一点 为坐标原点，

则向量 可用不共面的三个向量 表示：  eq \o\ac(○,1)1

因为 四点共面，据例4，有

设 ，

故

即             eq \o\ac(○,2)2

设

故                           eq \o\ac(○,3)3

于是

于是有

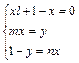
解得 ，

代入 eq \o\ac(○,1)1

得

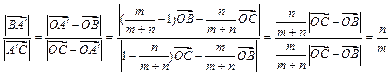
这说明 分线段 之比为

同理可证 ，

从而

 

例5．等腰三角形的中线垂直于底边。

证明：如图所示，取等腰三角形为 ，

记 ，

则

记中线 ，

则 。

故

据已知条件 即

故

即 。