知识点十二:立体几何中的向量方法
定义 如果直线垂直于平面内的每一条直线,则称直线
![]() 和平面
和平面
![]() 垂直,记为
垂直,记为
![]() 。
。
定理1 如果直线和平面内的两条相交直线垂直,那么直线和平面垂直。
已知:
![]() ,求证
,求证
![]() 。
。
证明:如图所示,
设为
![]() 平面
平面
![]() 内任一条直线,
内任一条直线,
在直线
![]() 和
和
![]() 上分别取不同于点
上分别取不同于点
![]() 的两点
的两点
![]() 和
和
![]() ,
,
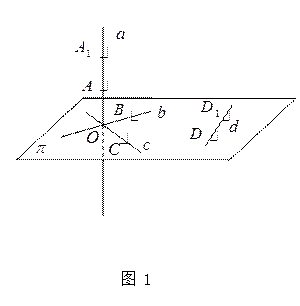
在
![]() 和
和
![]() 上各取不重合的两点
上各取不重合的两点
![]() ,
,
![]() ,
,
向量
![]() 和
和
![]() 不共线,
不共线,
则
![]() eq \o\ac(○,1)1
eq \o\ac(○,1)1
将
eq \o\ac(○,1)1式两边数乘向量
![]() ,
,
得
![]()
因为
![]() 和
和
![]() ,
,
所以
![]()
于是
![]() ,
,
由此知
![]() ,即
,即
![]() ,从而
,从而
![]()
例1 证明通过正方体的一个顶点的三条棱的另三个端点的平面垂直于正方体过这个顶点的对角线。

证明:如图所示,正方体正
![]()
往证
![]()
设
![]() ,
,
![]() ,
,
![]()
则
![]()
![]()
于是
![]()
![]()
由
![]() ,故
,故
![]()
因此
![]()
由此得出
![]()
类似地可以证明
![]()
故
![]()

例2.已知两条异面直线
![]() 和
和
![]() ,它们所成的角等于
,它们所成的角等于
![]() ,它们的公垂线
,它们的公垂线
![]() 的长度等于
的长度等于
![]() ,在已知直线
,在已知直线
![]() 和
和
![]() 上分别取点
上分别取点
![]() 和
和
![]() ,且
,且
![]() ,求
,求
![]()
如图所示,做向量
![]()
则
![]()
于是
![]() eq \o\ac(○,1)1
eq \o\ac(○,1)1
由于向量
![]() 垂直于向量
垂直于向量
![]() 和
和
![]() ,
,
所以
![]()
有两种情况
(1)
![]()
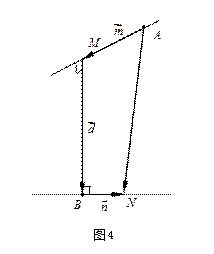
(2)
![]()
相应
![]() 有两种情况
有两种情况
(1)
![]()
(2)
![]()
故由式 eq \o\ac(○,1)1得
![]()
定义2 两个半空间,如果它们的边界是两个不平行的平面,那么它们的交叫做二面角。
定义3 二面角和垂直于它的棱的平面的交,叫做二面角的平面角。
定义4 二面角的平面角
![]() 的度数,叫做二面角的度数。
的度数,叫做二面角的度数。
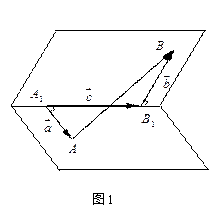
例3.线段的
![]() 端点属于大小为
端点属于大小为
![]() 的二面角的两个界面,
的二面角的两个界面,
![]() 和
和
![]() 到棱的距离分别为
到棱的距离分别为
![]() 和
和
![]() ,即
,即
![]() 和
和
![]() ,若
,若
![]() ,求
,求
![]()
解:设
![]()
则
![]()
故
![]()
由于
![]() ,
,
![]()
故
![]()
故
![]()
而
![]()
于是
![]()
例4.设
![]() 为任意一个四面体,
为任意一个四面体,
![]() 为
为
![]() 内部的任意一点,连接
内部的任意一点,连接
![]() ,延长之使其分别交对面于点
,延长之使其分别交对面于点
![]() ,
,

求证:
![]()
证明:取
![]() 为坐标原点,
为坐标原点,
设
![]()
则
![]() 可表为
可表为
![]()
由题设知
![]()
另外
![]()
![]()
由
![]() 共面,
共面,
得
![]()
而
![]()
故
![]()
![]() 线性无关
线性无关
得
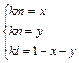
解得
![]()
因此
![]()
用同样的方法可证
![]()
所以
![]()
