模拟试题一 答案
一、填空题
1. ![]()
2. 全等的矩形
3. 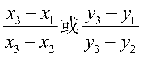
4. 完备
5. ![]()
二、选择题
1. A
2. A
3. A
4. C
5. C
三、简答题
答:众所周知,欧几里得《几何原本》是演绎体系的里程碑,虽然它不尽完善,但它确实是建立科学演绎体系的最早的代表作,它一经问世,就引起了学术界的广泛关注,欧几里得之后的数学家们在对《几何原本》的研究过程发现,它的第五公设的内容不象前四条公设叙述的那么简单,同时它又是在第二十九条命题之后才出现的,于是这些数学家很自然提出这样一个问题:是否底五公设它不是一条公理,而是一条命题呢?与是他们试图去论证第五公设的独立性,在这种论证过程中,罗巴切夫斯基与黎曼分别建立了新的无矛盾的科学演绎体系,即罗氏及何与黎曼几何,这两种几何与欧氏几何有共同的绝对几何公理体系,只是平行公理不同。
四、计算与证明题
1. 解:设正交变换为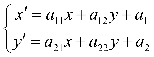
把对应点的坐标代入所设变换式,并利用正交变换式的系数关系得: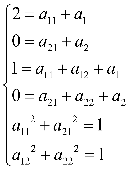
解这个方程组得: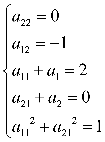
由![]() ,可得
,可得![]()
故所求正交变换为: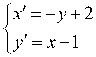 或
或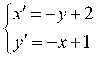 。
。
2. 证明:设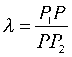 ,其中
,其中![]() 是分点,则
是分点,则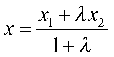 ,
,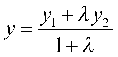
将![]() 分别代入直线方程
分别代入直线方程![]() ,解得
,解得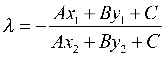 。
。
3. 解:(1) 不存在,因为无穷远点没有非齐次坐标。
(2) 存在,设![]() ,则这个点的非齐次坐标为2
,则这个点的非齐次坐标为2
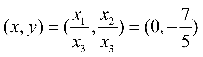
4. 解:
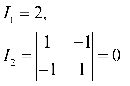
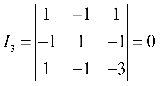
因为![]() , 所以为线心曲线。
, 所以为线心曲线。
它唯一的直径即中心线,也是主直径,其方程为:![]() ,取其为
,取其为![]() 轴,
轴,
再任取垂直与它的直线为![]() 轴,例如取
轴,例如取![]()
取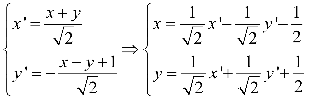 (为相应坐标变换公式)
(为相应坐标变换公式)
代入原曲线方程,得简化方程为![]() ,即
,即![]() 。
。