一、填空题

1. 

2. 

3. 自对应点

4. 共线 -1

5. 种差+邻近的属=被定义的概念

 

二、选择题

1. B

2. C

3. C

4. D

5. B

 

三、简答题

答：概括地说，几何学的公理化方法是从少数原始概念和公理出发，遵循逻辑原则建立几何学演绎体系的方法。用以推导出其它几何原理的不再加以证明的基本原理称为公理，用以解释其它概念而本身不再加以定义的概念称为原始概念，它们的性质由公理来制约，除了这些公理和原始概念外，其它定理和概念都必须由这些公理和原始概念逻辑地推到得出，这种方法就是公理法。公理法的结构由以下四部分组成：原始概念的列举；定义的叙述；公理的叙述；定理的叙述和证明。

 

四、计算与证明题

1. 解：设所求变换的逆变换为 。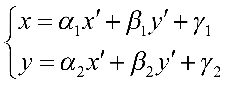

则直线变成，

由题设可知与表示同一条直线，

所以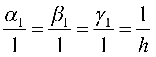（h为待定系数），故；

同理（k为待定系数）。

又因为点的象为原点，于是：

所以所求变换的逆变换式为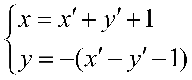

故所求仿射变换为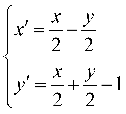

2. 证明：已知平面上任意四边形ABCD，设两组对边AB, CD与AD, BC 

分别交于点P, Q，在平面π之外任意选取一点O，设O与直线PQ所确定的平面为α，做与平面α平行的平面β，以为射影中心，做从平面π到平面β的中心射影，则在此中心射影下直线PQ是影消线，它的对应直线是平面β上的无穷远直线，由中心射影保持点线的结合性，故四边形ABCD的对应四边形A’B’C’D’满足：两组对边A’B’, C’D’与A’D’, B’C’分别交于无穷远点，所以四边形ABCD的对应四边形A’B’C’D’是平行四边形。

3. 解: 

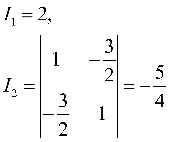，        系数矩阵：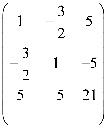

因为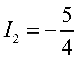, 所以为双曲型曲线。

其特征方程为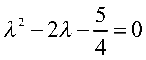

特征根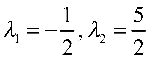

非渐近主方向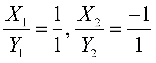 

x’轴: 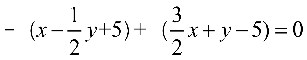 ，即

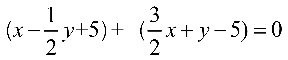y’轴:  ，即

取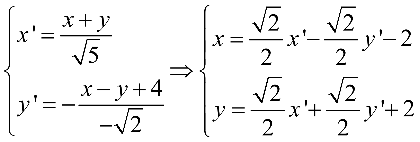（为相应坐标变换公式）

 

将其代入原曲线方程得简化方程为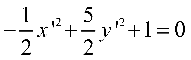，即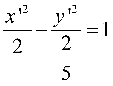。