数制与码制是数字系统功能实现的基础。将数字符号按序排列成数位，并遵照某种由低到高的进位方式计数来表示数值的方法，称为计数制。在数字系统中，要把十进制数转换成二进制数，并且为减小形成代码及传输错误，采用可靠编码。本章主要介绍数制及其变换，二进制数的表示与编码。

1.1 数制系统与数制

1.1.1 数制系统

今天的计算机主要应用四种数制系统：十进制、二进制、八进制和十六进制。每一种进制在不同的数据处理中都各有优点。在计算机的数制系统中，数的大小首先与其符号及其所在的位置决定。例如十进制数518有三个符号5、1、8和三个十进制位。其次，与数的读取顺序相关，数位可以从右到左升序读取，这时，最左端数位是最高有效位；也可以从左到右降序读取，最右端的数位是最高有效位。如十进制数518中，最高有效位是5，最低有效位是8。下面约定在没有特别声明时，本书的数制均按从右到左的升序机制实现。

1.1.2 数制

1. 十进制数

十进制是我们日常生活中经常使用的数制系统。其构成的数字符号有：0、1、2、3、4、5、6、7、8、9；符号位置的基础值为10，不同的位置以相应10的位置次幂即值权体现。例如，符号为5，其位置的权值为2（从右以0开始计数），十进制数值为5×102。表1-1给出了十进制权的排列。

这样，十进制数518可用符号与权表示为5×102+1×101+8×100。可见，在十进制中，每个权等于10的位置次幂，它的值等于符号与位置次幂的积。

2. 二进制数

 二进制是计算机运算的基础，它只有两个符号0与1，符号位置的基础值为2。二进制权的排列如表1-2。

例如，二进制数1101用符号与权表示为1×23+1×22+0×21+1×20。等价十进制数值为13，即1×23+1×22+0×21+1×20 = 13。

3. 八进制数

八进制数常常用于压缩方式表示二进制数，它的符号有：0、1、2、3、4、5、6、7，符号位置的基础值为8。八进制权的排列如表1-3。

例如，八进制数516用符号与权表示5×82+1×81+6×80。等价十进制数为334。

4. 十六进制数

十六进制数也是对二进制数的一种压缩表示形式，常用于程序设计中使用。十六进制符号有：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个。其中，A、B、C、D、E、F的十进制数分别表示为10、11、12、13、14、15。符号位置的基础值是16。十六进制权的排列如表1-4。

例如，十六进制数A16，用符号与权表示为A×162+1×161+6×160，等价十进制数为10×162 +1×161 +6×160，结果为2582。

一般地，N进制需要用到N个数码符号，符号位置的基础值为N，运算规律为逢N进一。N进制的M整数其用符号与权展开有如下表达式：

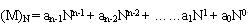
式中N为基础值，an-1、an-2、……a1、a0为符号。

由权展开式所得到的结果，就是将一个N进制数转换为十进制数的值。

1.2 数制变换

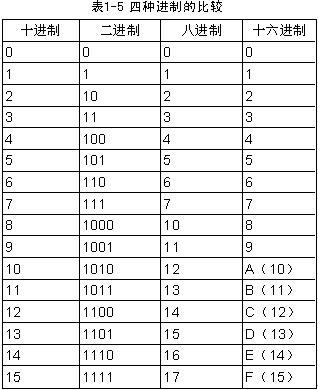
不同进制的数彼此可以相互转化，从一个进制的数转化为另一个进制的等价数。事实上，上面介绍的各种进制数按符号与权展开所表示的数值就等价于十进制数。下面表1-5给出了十进制、二进制、八进制与十六进制部分比较。

1. 从其它进制到十进制的转化

从其它进制到十进制的转化通常使用的方法是以符号和权的方式展开即可实现。
例如，二进制数110011转化为十进制数为：

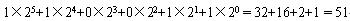
八进制数116转化为十进制数为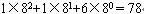

十六进制数4E转化为十进制数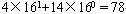

2. 从十进制到其它进制的转化

从十进制到其它进制的转化，常用的方法可使用进制数作除法求余数来实现。
例如，十进制数51转化为二进制数：

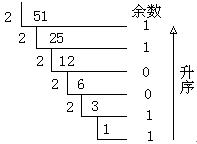
十进制数78转化为八进制数：

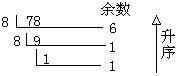
十进制数78转化为十六进制数：

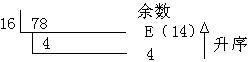
3. 其它进制间的相互转化

其它进制间的相互转化可以先转化为十进制数，再转化为相应的进制来实现。这是通用的转化方法，但是，二进制、八进制和十六进制之间由于权存在着2的幂次关系，所以，相互之间的转化存在简便方法。

例如，八进制数116转化为二进制数：

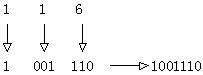
在这里八进制数116的最高位1的二进制数仍然是001，但由于最高位前的0无意义，所以去掉了。

十六进制数4E转化为二进制数：

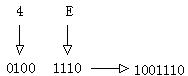
二进制数110011转化为八进制数：

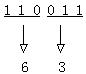
在这里每三个二进制符号表示一个八进制符号，因为八进制符号位置的基础值是8，为2的三次幂。所以，三个二进制符号表示一个八进制符号，最高位不足三位由0补足。

二进制数110011转化为十六进制数：

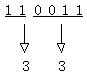
与八进制转化为二进制原理相同，二进制数转化为十六进制数可以从最低位起，每四个符号为一组，最高位不足四位由0补足。

八进制数与十六进制数相互转化，可以先转化为二进制数，再进行转化。

1.3 进制数的表示

在数字系统的处理中，使用和存储二进制数有两种格式：一是无符号数；二是有符号数。无符号的数即是没有“+”或“-”号的二进制数，指的是正数；有符号的数可以是正数也可以是负数。在计算机中通常使用三种格式表示有符号数。一是符号-绝对值；二是反码；三是补码

1.3.1 无符号数

在计算机中，使用缓存区来表示和存储数字信息，由于缓存区的空间是有限的，所以，也限制了表示和存储数字信息的大小。一个给定值的所有信息必须存入缓存区这个空间中，包括其正号与负号。如果给定值没有符号即是正值。对于16位缓存区表示或存储正值，其范围是从0~65535之间的任何数。如图1-1所示。

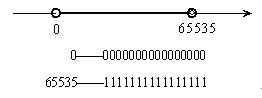
图1-1 无符号数的表示

但是，在缓存区中表示和存储的数具有模运算的特点，表现在当最大数值加1后，又回到0值。如同日常生活中使用的时钟。仍然对16位缓存区而言，当把十进制数51表示和存储于缓存区中，应如何进行呢？通常的方法是先把十进制数51转换为二进制数；然后把二进制数左端的空余位用0补足至16位。具体过程如下：

1)十进制数51转换为二进制数110011

2)用0补足二进制数110011左端的空余位到16位。即0000000000110011。

1.3.2 有符号数

有符号数比无符号数的表示和存储要复杂得多。通常的方法有符号-绝对值、反码和补码。

1. 符号-绝对值

符号-绝对值表示是以最高位保留作符号位使用。如果最高位是0，表示该数为正值；如果最高位是1，表示该数是负值。在这种表示法中，0有两种表示“+0”和“-0”，但其值都为0值。对于16位缓存区，由于符号位占用一位数值位，所以，只有15位用于表示和存储数字信息。如图1-2所示。

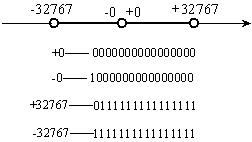
图1-2 符号-绝对值表示

由十进制数转换到符号-绝对值表示：

1) 将十进制数按其绝对值转换为二进制数；

2) 除二进制数最左端一位外，由0填充到缓存区的位数；

3) 如果该数是正值，二进制数最左端一位由0填充；如果是负值，二进制数最左端一位由1填充。

例如：将-51变换为符号-绝对值表示。（缓存区为16位）

-51的绝对值是51，转换为二进制数110011；留110011最左端一位，其余填充0至16位；因负数，110011最左端一位填1。其符号-绝对值表示为1000000000110011。

2. 反码

在反码中，所有的位都参加符号的表示。反码是一个对称系统，一个数和它的补成对出现。一个数与它的补的和运算为0。而一个数的补只要把该数的所有数位取反即可得到。通常对正数按符号-绝对值表示，负数按正数各位取反得到。反码用于数据通信的数据校验，以验证数据传输的正确性。如图1-3所示。

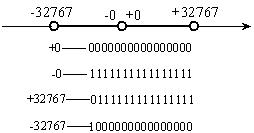
图1-3 反码表示

十进制数的反码表示步骤如下：

1) 将十进制数绝对值转换为二进制数；

2) 用0填充二进制数左边的所有空余位至缓存区位数；

3) 如果该数为正数，反码表示完成；如果为负数，则对每个数位取反（0变1；1变0）。

例如：-51的反码表示

将-51转换为二进制数110011；表示为符号-绝对值为0000000000110011；由于为负数，将各位取反1111111111001100。

3. 补码

补码同反码一样，都是各数位参与符号的变化。但是，它是一个非对称系统，只有一种0表示。这样便多出一个额外的负数（-32768）。如图1-4所示。

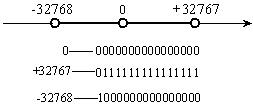
图1-4 补码表示

十进制数的补码表示步骤如下：

1) 将十进制数的绝对值转换为二进制数；

2) 用0填充二进制数左边所有空余位至缓冲区的位数；

3) 如果该数为正的，则完成；如果该数为负的，则对每个数位取补（将0变1；1变0），同时，将结果加1。如果加1的结果导致最高位上出现进位，则丢弃。

例如：将-51表示为补码。

-51的绝对值为51，转换为二进制数110011；对二进制数110011左端填充0至16位缓冲区数位0000000000110011；由于为负数，对该数取补得到1111111111001100，在对其加1运算得到补码1111111111001101。