2.4.2 基本公式

逻辑代数有一系列的定律和规则，用它们对逻辑表达式进行处理，可以完成对电路的化简、变换、分析和设计。

表2-3给出了逻辑代数的基本公式。这些公式也叫布尔恒等式。

表2-3 逻辑代数的基本公式

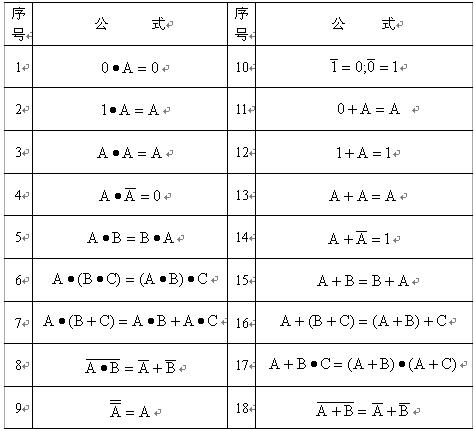
式(1)、(2)、(11)和(12)给出了变量与常量间的运算规则。

式(3)和(13)是同一变量的运算规律，也叫重叠律。

式(4)和(14)表示变量与它的反变量之间的运算规律，也称为互补律。

式(5)和(15)为交换律，式(6)和(16)为结合律，式(7)和(17)为分配律。

式(8)和(18)是著名的德?摩根(De?Morgan)定理，亦称反演律或反演定理。这一公式在逻辑函数的化简和变换中经经常要用到。

式(9)表明，一个变量经过两次求反运算之后还原为其本身，所以该式又称还原律。

式(10)是对0和1求反运算的规则，它说明0和1互为求反的结果。

这些公式的正确性可以用列真值表的方法加以验证。如果等式成立，那么将任何一组变量的取值代入公式两边所得的结果应该相等。因此，等式两边所对应的真值表也必然相同。
【例1】 用真值表证明表2-3中式(17)的正确性。

解：已知表2-3中的式(17)为

 A+B?C＝(A十B)? (A十C)

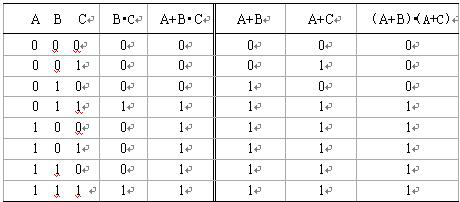
将A、B、C所有可能的取值组合逐一代入上式的两边，算出相应的结果，即得到下面的真值表。可见，等式两边对应的真值表相同，故等式成立。

表2-4式（17）的真值表

    

2.4.3 若干常用公式

表2-4中列出了几个常用公式。这些公式是利用基本公式导出的。可以给化简逻辑式的工作带来很大方便。

表2-4 若干常用公式

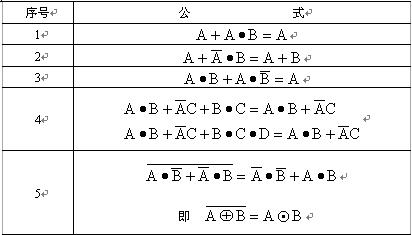
现将表2-4中的各式证明如下。

证明： A十A?B＝A

证：   A十A?B＝A?(1十B)＝A?1＝A

上式说明在两个乘积项相加时，若其中一项以另一项为因子，则该项是多余的，可以删去。

证明：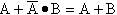

证：

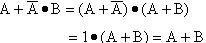
这一结果表明，两个乘积项相加时，如果一项取反后是另一项的因子，则此因子是多余的，可以消去。

证明：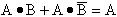

证：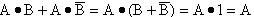

这个公式的含意是当两个乘积项相加时，若它们分别包含原变量和其反变量两个因子而其他因子相同，则两项可合并，且可将原变量和反变量两个因子消去。如上例中的B和B(—)合并消取。

证明：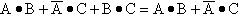

证：

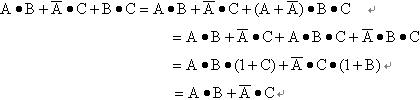
这个公式说明，若两个乘积项中分别包含A、 两个因子，而这两个乘积项的其余因子组成第三个乘积项时，则第三个乘积项是多余的，可以消去。

从上式不难进一步导出 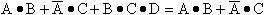这一结果

证明：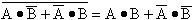

证：根据德?摩根定理可知

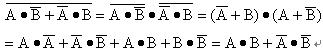
从以上的证明过程可以看出，这些常用公式都是由基本公式推导得出的结果。显然还可以推导出更多的公式。因为表2-4中的几个公式用的比较多，所以把它们特意列出。直接引用这些公式将有助于简化推演过程。