2.4.4 基本规则

1. 代人规则

在任何一个逻辑等式中，如果将等式两边出现的某变量A，都用一个逻辑式代替，则等式依然成立，这个规则称为代入规则。

因为任何一个逻辑式也和任何一个逻辑变量一样，只取二元常量0或1，所以代入规则是正确的。

例如，在B(A+C)=BA+BC中，将所有出现A的地方都代以逻辑式A+D，则等式仍成立，
即得

B[(A+D)+C]=B(A+D)+BC=BA+BD+BC

2. 反馈规则

根据摩根定律，求一个逻辑式L的反逻辑式 时，可以将L中的与(?)换成或(十)，或(十)换成与(?)；再将原变量换为非变量(如A换为 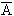)，非变量换为原变量；并将1换成0，0换成1；那么所得的逻辑式就是 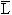。这个规则称为反演规则。 

利用反演规则，可以比较容易地求出一个逻辑式的反逻辑式。注意变换时要保持原式中“先括号、然后与、最后或”的运算次序，否则容易出错。例如，要求 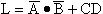的反逻辑式 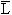时，按照上述法则，得  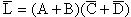，而不能写成  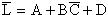。另外不属于单个变量上的反号应保留不变。

3. 对偶规则

L是一个逻辑表达式，如把L中的与(?)换成或(十)，或(十)换成与(?)；1换成0，0换成1，那么就得到一个新的逻辑式，这就是L的对偶式，记作L'。 。例如 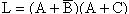， ，则 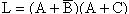变换时仍需注意保持原式中的运算次序。

所谓对偶规则，是指当某个逻辑恒等式成立时，则其对偶式也成立。

根据对偶规则，有时为了证明两个逻辑式相等，可以通过证明它们的对偶式相等来完成，因为有些情况证明它们的对偶式相等更加容易。例如

试证明表2-3中的式（17），即

A+BC=(A+B)(A+C) 

证明：首先可写出等式两边的对偶式，它们分别是

 A(B+C)和AB+AC

根据乘法分配律即可看出这两个对偶式是相等的，即A(B+C)=AB+AC。由对偶规则可知，原来的两式也相等，于是式（17）得到证明。