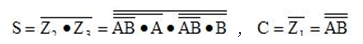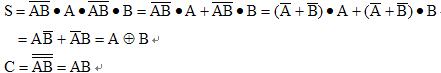逻辑电路按输入输出信号的关系，分为组合逻辑电路和时序逻辑电路两大类。本章首先介绍组合逻辑电路。

3.2.1 组合逻辑电路的特点

逻辑电路按其输出信号对输入信号响应的不同可以分为组合逻辑电路和时序逻辑电路两大类。

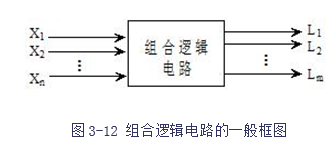
若逻辑电路在其任一时刻的输出仅取决于该时刻输入变量取值的组合，而与电路以前的状态无关，则该逻辑电路就称为组合逻辑电路（简称组合电路）。图3-12给出了组合逻辑电路的一般框图，从图中可看到，当输入变量X的取值（共有种可能的组合状态）确定以后，输出变量Li（m个）的取值便随之而定，因而输入与输出之间乃是一种函数关系，我们将这种函数关系称为逻辑函数，写作

从电路的结构和功能上看，组合逻辑电路具有如下特点：

（1）电路中不存在输出端到输入端的反馈通路。

（2）电路主要由各种门电路组合而成，其中不包含存储信息的记忆元件。

（3）电路的输入状态一旦确定后，输出状态便被惟一地确定下来。所以,输出变量是输入变量的逻辑函数。

（4）电路的输出状态不影响输入状态，电路的历史状态也不影响输出状态。

3.2.2 组合电路的一般分析方法

对给定的组合逻辑电路图，求解其逻辑功能的过程称为组合逻辑电路的分析。所谓分析，就是找出组合逻辑电路输入、输出之间的关系，也就是找出何种输入状态组合下电路输出为1、何种输入状态组合下电路输出为0。通过分析，可以了解组合逻辑电路的功能和设计思路，从而进一步对电路作出评价和改进。

通常，只要列出组合逻辑电路的真值表，就可以知道该电路的逻辑功能。因此，组合逻辑电路的分析，实质上是由逻辑函数的逻辑图形式入手，通过逻辑表达式，最终转换成函数的真值表形式的过程。

组合逻辑电路的一般分析可按如下步骤进行：

第一步：根据给出的组合逻辑电路电路图，由输入端逐级向后递推，写出每个门的输出对于输入的逻辑关系，最后得到整个组合逻辑电路的输出变量对于输入变量的逻辑函数表达式。

第二步：利用逻辑代数法或卡诺图法，对所得的逻辑函数表达式进行转换或化简，得到逻辑函数的标准表达式或最简表达式。

第三步：由逻辑函数的标准表达式或最简表达式列出对应的真值表。

第四步：由真值表判断出组合逻辑电路的逻辑功能。

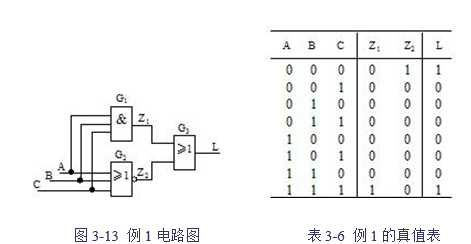
【例1】试分析图3-13所示的组合逻辑电路的功能。

解：（1）由G1、G2、G3的各个门电路的输入、输出关系，推出整个组合逻辑电路的表达式：Z1=ABC，Z2=，F=Z1+Z2= ABC+。

（2）对该逻辑式进行化简：第四步：由真值表判断出组合逻辑电路的逻辑功能。

（3）根据化简后的函数表达式，列出如表3-6所示的真值表。

（4）从真值表中可以看出，当A、B、C三个输入一致时（或者全为0、或全为1），输出才为1，否则输出为0。所以，这个组合逻辑电路具有检测“输入不一致”的功能，也称“不一致电路”。

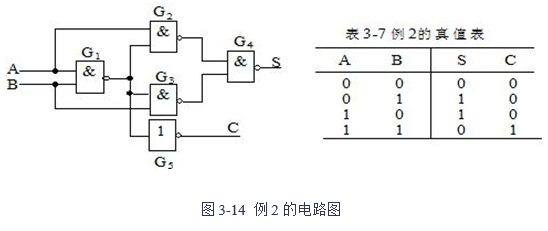
【例2】试分析图3-14所示的组合逻辑电路的功能。

解：（1）由G1、G2、G3、G4、G5各个门电路的输入、输出关系，推出整个组合逻辑电路的表达式：Z1=，Z2= =，Z3= =

（2）对该逻辑表达式进行化简：

（3）根据化简后的函数表达式，列出如表3-7所示的真值表。

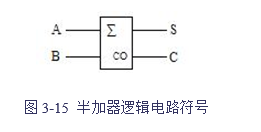
（4）若设A、B各为一位二进制加数，则从真值表中可以看出，S为两加数相加后的一位和、C为两加数相加后的进位值。由此可见，这个组合逻辑电路实现了加法器的功能。由于这种加法器不计低位来的进位，所以称它为“半加器”。半加器是运算器的基本单元电路，其符号见图3-15。