逻辑设计是数字电路技术中的一个重要课题。任何一个可描述的事件或过程，都可进行严格的逻辑设计。根据要求规定的逻辑功能，通过抽象和化简，进而求得满足功能要求的组合逻辑电路图的过程，称为组合逻辑电路的设计。可见，组合逻辑电路的设计是分析的逆过程。

3.3.1组合逻辑电路的一般设计方法

一般组合逻辑电路的设计可按如下步骤进行：

第一步：根据所需的功能的要求和条件，弄清输入、输出变量的个数及它们之间的逻辑关系，列出满足逻辑要求的真值表。

第二步：由真值表列出逻辑函数的标准“与或”式或最简表达式。

第三步：根据所选的门电路类型及实际问题的要求，将逻辑函数转换成所需的表达式形式。

第四步：由所得的逻辑表达式画出逻辑电路图。

以上步骤中，关键的是第一步。一个事件或过程的功能描述，最初总是以文字的形式提出的，设计者必须对这些描述有全面、正确的理解。只有先弄清哪些是输入变量、哪些是输出变量，以及输入、输出变量之间的逻辑关系，才能列出正确的真值表。正确的真值表是组合逻辑电路设计的基础。

需要指出的是，一个最简的逻辑表达式不一定就对应一个最简的逻辑电路。当采用中、小规模集成电路（一片包括数个门至数十个门）产品，因此应根据具体情况,尽可能减少所用的器件数目和种类，这样可以使组装好的电路结构紧凑，达到工作可靠而且经济的目的。

    

3.3.2 组合逻辑电路设计举例

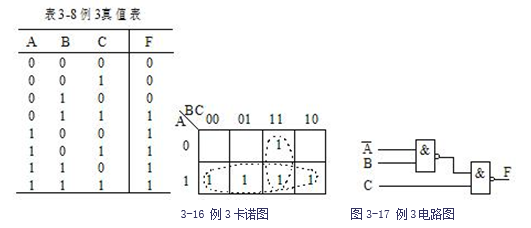
【例3】三人按少数服从多数原则对某事进行表决，但其中一人有决定权,即主要他同意，不论同意者是否达到多数，表决仍将通过。试用“与非门”设计该表决器。

解：（1）由题意可知该表决器有三个输入变量和一个输出变量。设A、B、C为输入变量（1表示同意，0表示不同意），且A为有决定权的变量，L为输出变量（1表示通过，0表示不通过）。将表决器的逻辑功能描述为：当A为1或B、C均为1时，L才为1，否则L为0。由此，可以列出真值表如表3-8所示。

 （2）由真值表列出逻辑表达式为:            用卡诺图化简此逻辑式（如图3-16所示），得到最简“与或”表达式 L=A+BC.

（3）将表达式转换成用“与非”逻辑实现的形式 

（4）根据逻辑表达式画出如图3-17所示的逻辑电路。这里假设系统能提供所有的原、反变量，否则还需增加一个“非门”以实现。

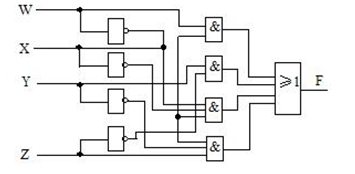
【例4】人类有四种血型，A、B、AB和O型。AB型可以接受任何血型，但它只能输给AB型；A型能输给A型或AB型，可以接受A型或O型；B型能输给B型或AB型，可以接受B型或O型；O型能输给所有血型，但只能接受O型。设计一个血型检测器。 

解：（1）首先，把实际问题转化为逻辑问题。由题意可知,该检测器具有四个输入变量和一个输出变量。输入变量表示输血和受血的血型，当受血者能接受时，输出变量为1，否则为0。用变量WX表示输血，YZ表示受血。这样，四种血型编码表示如下： WX=00为A型，YZ=00为A型，WX=01为B型，YZ=01为B型，WX=10为AB型，YZ=10为AB型，WX=11为O型，YZ=11为0型。 

（2）由题意条件列出真值表，如表3-9所示

（3）由表3-9得到图3-18卡诺图。

对卡诺图3-18化简得到逻辑表达式：

（4）由逻辑表达式画出逻辑图3-19：

图3-19 例4逻辑图