时序逻辑电路的分析与设计是数字逻辑电路应用的基础。生产实际应用中控制输出，不仅与当时的输入有关，常常还与输入前的状态有关，使其应用具有一定的记忆性。本章重点阐述时序逻辑电路的分析与设计的经典方法，尤其对中小规模逻辑电路的分析与设计。

5.1 时序逻辑电路概述

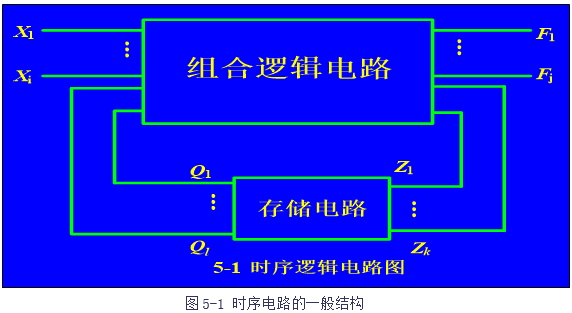
在数字电路中,存在两种类型的电路。一是组合逻辑电路；二是时序逻辑电路。组合逻辑电路的特点是电路的输出仅由电路的当时输入状态决定。时序逻辑电路的输出不仅由电路当时的输入状态作用，而且还由输入以前的状态影响，表现电路的输出既与现在状态变量有关，还与电路记忆的状态变量有关。输出函数是当前状态变量与电路记忆的过去状态变量的逻辑函数。从电路结构上看，是组合逻辑电路与存储电路共同作用的结果。如图5-1给出了时序逻辑电路的一般结构图。时序逻辑电路在结构上通常由两部分组成，一是包含存储电路，二是由存储电路构成反馈。

在时序电路中，输入逻辑变量有两部分：一是时序电路的输入，二是内部电路的输入；输出逻辑变量有两部分：一是时序电路的输出，二是内部电路的输出。内部电路的输入与输出变换是经过存储电路实现的。通常，时序电路的输入是指外部的输入，时序电路的输出是指外部电路的输出。而时序电路的状态是指存储电路的输出或内部电路的输入，其内部电路的输出称为驱动或激励。事实上，时序逻辑电路通过存储电路引入了反馈机制。时序电路的函数关系如下：

时序电路输出=f(时序电路输入，内部电路输入)

驱动或激励=g(时序电路输入，内部电路输入)

存储电路的次态输出=h(存储电路输入，存储电路的现态)

存储电路通常由触发器电路构成，存储电路的现态（用Qn+1表示）是触发器时钟动作前的状态，即所记忆的状态；次态（用Qn表示）则是触发器时钟动作后的状态，是存储电路输入与现态共同作用结果的状态。在时序电路中，通常有多个触发器，按照触发器的动作特点分为同步时序逻辑电路和异步时序逻辑电路。同步时序逻辑电路中所有触发器状态的变化是在同一时钟信号下同时动作；异步时序逻辑电路其存储电路中的触发器状态的变化不是在同一时钟下进行的，动作的步调是不一致的。

此外，根据输出信号的特点,可以把时序逻辑电路分为Mealy型和Moore,Mealy型时序逻辑电路输出变量由存储电路的状态和输入变量共同决定；Moore型时序逻辑电路输出变量仅由存储电路的状态决定,通常没有输入变量。它是Mealy型时序逻辑电路的一种特例。

5.2 时序逻辑电路的描述方法

由于时序逻辑电路输出是电路的输入与电路现态共同作用的结果，它不象组合逻辑电路，输出仅是输入（现态）函数。这样在描述时序逻辑电路时，就很少使用适合于组合逻辑电路的真值表、逻辑函数、卡诺图等方法。为了揭示时序电路的内在时序关系，常用的方法有方程法、状态表/状态转换表、状态图/状态转换图、时序图方法等。

1.方程法

方程法是描述小规模时序逻辑电路的有效的方法，它直接从电路的结构分析中列出电路的各种函数关系，从而求解出逻辑电路的输出。在上一节，从时序逻辑电路的一般结构中分析出三个函数关系，这三个函数关系就构造了时序电路的三个方程：

由驱动或激励=g(时序电路输入，内部电路输入)构造了驱动方程或激励方程

由存储电路的次态输出=h(存储电路输入，存储电路的现态)构造了状态方程

由时序电路输出=f(时序电路输入，内部电路输入)构造了输出方程

在这里函数关系g、h、f是依电路结构而定的。

2.状态表/状态转换表

状态表是反映时序逻辑电路次态与现态的转换表。通常由电路的状态数构造表的行,由输入信号的组合数构造表的列。对于Moore型电路时，该表仅有次态和现态表项，没有输入表项。状态表主要揭示了时序逻辑电路在时钟的作用下，电路次态与现态的转换关系。

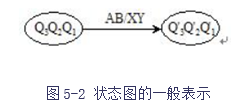
3.状态图/状态转换图

状态图是状态表的图形化表示，通常用圆圈表示某一状态，有向线段表示状态的变换，有向线段上的标识表示状态转换的条件（输入变量取值/输出值）。如图5-2所示。

状态表与状态图是分析时序逻辑电路的主要方法，尤其对于中规模以上的时序逻辑电路的分析更为重要。

4.时序图

时序图通常由仿真软件或实验所绘制的波形图，用于电路功能的检测。在时钟的作用下，电路的状态及其输出随时间的变化规律。