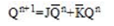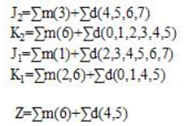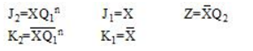5.4 同步时序逻辑电路的设计

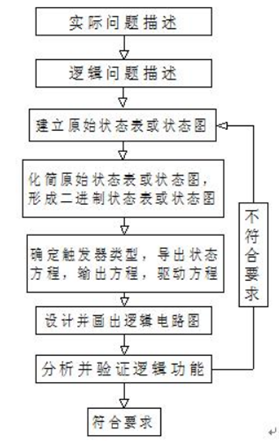
时序逻辑电路的分析是对给定的逻辑电路进行逻辑性能研究，以此说明逻辑电路的功能。然而，在实际应用中，通常会根据具体需要，设计一个逻辑电路，以完成某些逻辑功能。事实上，逻辑时序电路的分析是其设计的逆过程。其一般步骤如下：

1.根据逻辑功能要求，把实际问题转化为逻辑问题，并建立原始状态表或状态图

2.化简原始状态表或状态图。

3.对简化的状态表或状态图进行状态分配与编码，即进行二进制状态表的转化，以此得到逻辑电路的状态表或状态图。

4.选择触发器类型，并由电路状态数确定最小触发器数，导出状态方程，列出输出方程，确定驱动方程。

5.根据输出方程和驱动方程设计并画出逻辑电路图。

6.最后对逻辑电路图进行逻辑分析，以验证其逻辑功能。

其流程图如下：

上面是时序逻辑电路设计的基本步骤，在实际应用中，可根据具体情况进行适当调整。下面结合具体实例来说明时序逻辑电路的设计方法。

【例5】 用JK触发器设计一个110数字序列检测器。

该题目的实际要求很接近逻辑问题。由题意可知，该电路应有一个输入变量X和一个输出变量Z。当输入的数字序列包含110时，输出变量Z置1，否则为0。这样，电路的输出不仅与输入有关还与电路状态有关，可设计为一mealy型同步时序逻辑电路

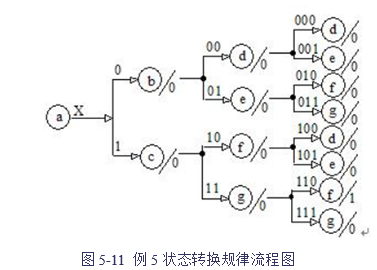
根据题意，确定电路原始状态转换规律。列出不同的输入变量X下，电路状态变化规律与输出变量Z的值。其状态转换规律流程图5-11。

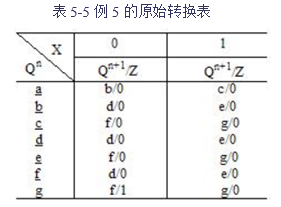
在图中，a为初始状态，X输入为0时，状态转换为b；输入为1时，状态转换为 c，此时的输出Z为0。同理，在状态b时，输入0进入状态d；输入1进入状态e，此时输出仍为0。在状态c时，输入0进入状态f；输入1进入状态g，此时输出仍为0。在d、e、f、g状态下，输入0或1，应与d、e、f、g状态比较，看是否存在新的状态，如果与前一状态相同即用前一状态表示，如果存在序列110输出Z即为1。由上面流程图的分析，画出原始状态表5-5如下：

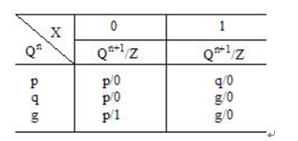
在原始状态图中，下划线的状态可以进行合并，得到简化的状态表5-6。

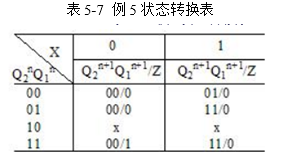
由简化状态表可知，电路状态共有三个，记为S0(p)、S1(q)、S2(g)。三个状态所需计数状态最小数为4，可选两个JK触发器（N≦22）。两个触发器的状态Q2Q1共有00、01、10、11，所以，可在这四种状态中任选三种。这里选取S0=00，S1=01，S2=11。构造出状态转换表5-7。

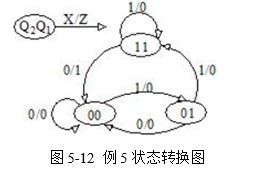
根据状态转换表画出状态图如图5-12所示。

 由状态图，根据JK触发器特征方程：

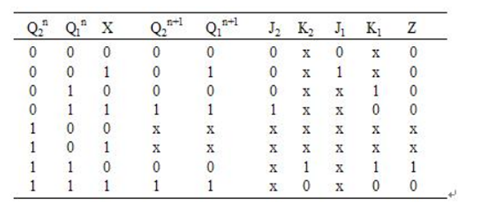
列出驱动方程和输出方程真值表5-8。

表5-8 例5驱动方程和输出方程真值表

驱动方程和输出方程的逻辑表达式如下：

式中∑m为最小项之和，∑d为无关项之和。利用卡诺图化简，得到最简的驱动方程和输出方程如下：

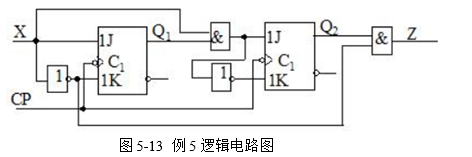
    由驱动方程和输出方程画出逻辑电路图如图5-13所示。

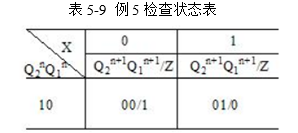
最后对电路进行检验，检验一是电路的功能是否符合要求；二是电路可否能自启动。在这里，对电路进行分析得知电路功能符合要求。在本设计中，由于存在“10”无关状态，所以要检查电路可否由10状态转入有效状态。其检查状态表5-9如下：

可见，设计电路功能符合要求，并且能够自启动。