轴心压杆可能破坏形式 |
| 强度 |
| 整体稳定 |
| 局部稳定 |
| 刚度 |
第五章拉杆、压杆和柱
第三节实腹式轴心受压构件的整体稳定
|
|
轴心受压构件的截面如无削弱,一般不会发生强度破坏,因为整体失稳或局部失稳总发生在强度破坏之前,轴心受压构件的截面如有削弱,则有可能在截面削弱处发生强度破坏,整体失稳破坏是轴心受压构件的主要破坏形式。
一、理想杆件的屈曲形式
所谓理想轴心压杆,须满足以下几个条件:
1)截面的形心纵轴是一直线
2)压力的作用线与形心纵轴重合
3)杆件为等截面
4)材料是完全均匀和弹性的
对于理想轴心压杆,其整体失稳的破坏形式与截面形式有密切关系,与构件的细长程度有时也有关系,一般情况下,可能发生以下几种屈曲形式:
1)弯曲失稳:
双轴对称截面,如I字形截面,H形截面(如图所示)
2)弯扭失稳:
单轴对称截面,如不对称I字形截面,[形截面,T形截面等绕对称轴的失稳,但上述截面形式绕不对称轴的失稳仍为弯曲失稳(如图所示)
3)扭转失稳:
十字形截面和Z形截面(如图所示)
二、理想杆件的临界应力(如图所示)
根据欧拉理论,理想压杆的弹性微分方程为:
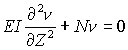
结合边界条件,解上述微分方程,可得:
欧拉临界力: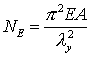 ;,这就是著名的欧拉公式
;,这就是著名的欧拉公式
相应的应力为: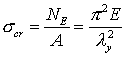 ;,称为欧拉临界应力
;,称为欧拉临界应力
如[弹出-交互图5-5a]中曲线1所示,当![]() ;时,压杆维持直线平衡状态;
;时,压杆维持直线平衡状态;![]() ;时,压杆处于曲线平衡状态,出现了平衡分枝现象,称之为屈曲。
;时,压杆处于曲线平衡状态,出现了平衡分枝现象,称之为屈曲。
欧拉临界应力与长细比的关系曲线(如图所示)
当压杆处于弹性阶段时,E为常量,而压杆处于非弹性失稳时,弹性模量E发生变化,须由香莱理论来解决压杆稳定问题,详见(如图所示)所示,为了简化计算,常用切线模量临界力作为压杆失稳的依据,与欧拉公式的推导一样,可得:
切线模量临界力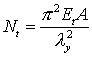 ;
;
切线模量临界应力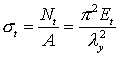 ;
;
其中:![]() ;为切线模量
;为切线模量
除切线模量理论外,研究压杆非弹性失稳还有双模量理论,折算模量理论,钢结构中常用的是切线模量理论。
三、影响压杆稳定的主要因素
1.残余应力
由于各种因素,如轧制、焊接、切割等均在压杆截面上产生残余应力,特别对于焊接结构,焊接残余应力尤为严重。
①不同轴线失稳残余应力影响不同(如图所示)绕强轴残余应力时![]() ;的影响比绕弱轴小
;的影响比绕弱轴小
②长细比![]() ;增大,残余应力对
;增大,残余应力对![]() ;的影响下降
;的影响下降
③钢材强度愈高,残余应力对![]() ;的影响下降
;的影响下降
2.初变形影响
包括初弯曲和初扭曲,实际轴压杆的纵轴不可能是一直线
3.初偏心影响
压力作用点与截面形心存在偏心,即存在N,M,对![]() ;产生影响,但钢结构设计规范中未加考虑,而桥梁规范中考虑了这一因素。
;产生影响,但钢结构设计规范中未加考虑,而桥梁规范中考虑了这一因素。
4.截面形状的影响
双轴对称截面:弯曲失稳
单轴对称截面:弯扭失稳
弯扭失稳对![]() ;影响比弯曲失稳大
;影响比弯曲失稳大
5.支座条件
由于![]() ;与长细比
;与长细比![]() ;有关,而
;有关,而![]() ;,其中
;,其中![]() ;为杆件的计算长度,对于不同的支座条件,其
;为杆件的计算长度,对于不同的支座条件,其![]() ;的值是不同的。
;的值是不同的。
![]() ;
;
其中:l——杆件的实际长度
![]() ;——计算长度系数,(如图取值)
;——计算长度系数,(如图取值)
由于上述因素的影响,使压杆一受压就发生弯曲,不存在由直线平衡到弯曲平衡的分枝点,因此也不存在屈曲临界力。
四、实际杆件的临界应力
由于残余应力、初弯曲、初偏心、截面形状、支座条件的影响,使得压杆的稳定极限承载力低于理想轴压杆,根据大量的试验数据,得到多条柱子曲线,所谓柱子曲线,就是反映稳定系数![]() ;和长细比
;和长细比![]() ;关系的曲线,我国钢结构设计规范将柱子曲线分为a,b,c三组(高层钢结构增加了d曲线),(如图所示)(如图所示)
;关系的曲线,我国钢结构设计规范将柱子曲线分为a,b,c三组(高层钢结构增加了d曲线),(如图所示)(如图所示)
分别给出了Q235钢,![]() ;钢和
;钢和![]() ;钢a,b,c三条柱子曲线的数值,设计时直接查表即可。不同的截面分类,不同的对称轴,所对应的曲线类别是不同的,可直接由查得曲线类别。
;钢a,b,c三条柱子曲线的数值,设计时直接查表即可。不同的截面分类,不同的对称轴,所对应的曲线类别是不同的,可直接由查得曲线类别。
求稳定系数![]() ;的步骤:
;的步骤:
1.先求出长细比![]() ;
;
2.(见表),确定压杆的柱子曲线类别
3.根据不同的曲线类别,(见表)
得稳定系数![]() ;
;
稳定系数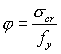 ;,求出稳定系数,实际杆件的临界应力即可求出,即:
;,求出稳定系数,实际杆件的临界应力即可求出,即:![]()
五、实腹式压杆整体稳定计算公式
考虑一定的安全系数,实腹式压杆整体稳定计算公式为:
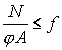 ;(5-3)
;(5-3)
其中:![]() ;——压杆的稳定系数,是长细比
;——压杆的稳定系数,是长细比![]() ;的函数
;的函数
A——压杆的毛截面面积