第四章 弯曲内力 习题
概念题
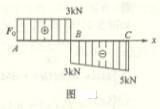
4.1
4.2
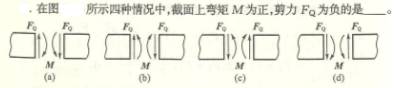
4.3
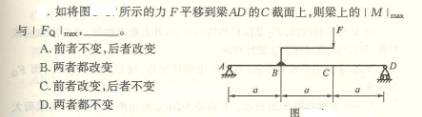
4.4
4.5
4.6
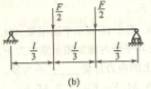
4.7
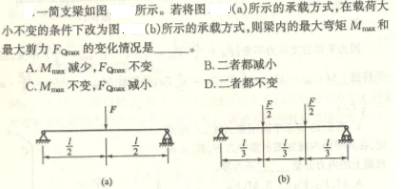
4.8
4.9
4.10
4.11
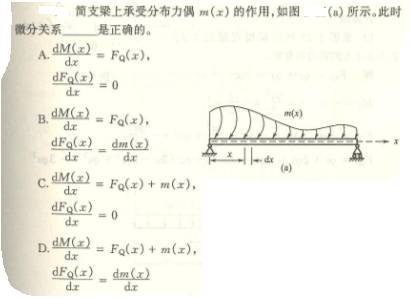
4.12
计算题
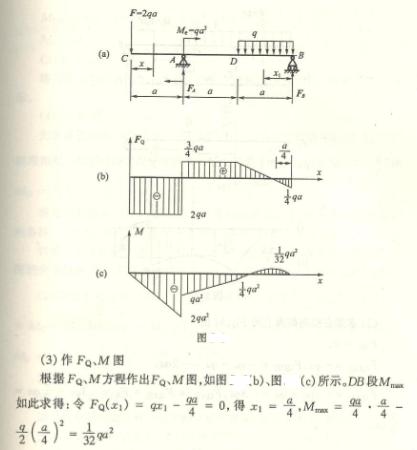
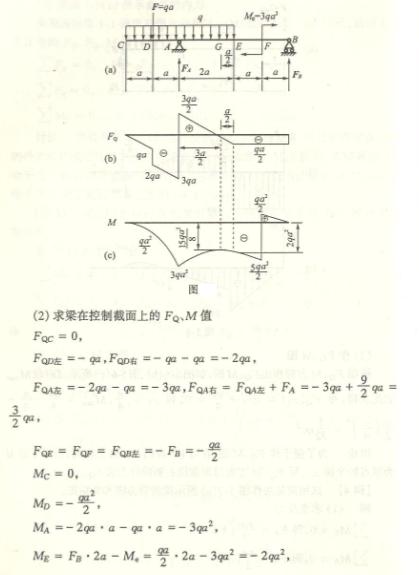
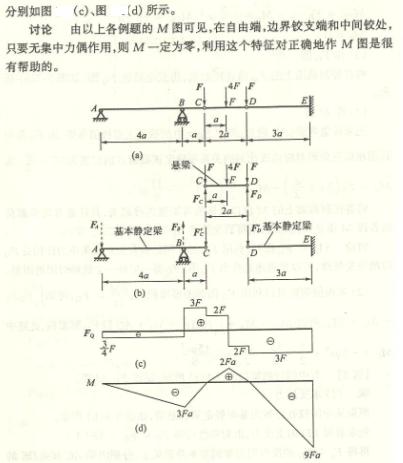
4.1
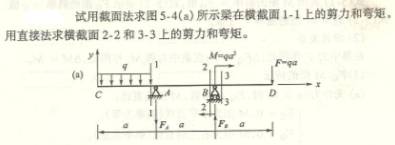
4.2
4.3
4.4
4.5
4.6
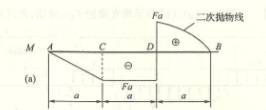
4.7
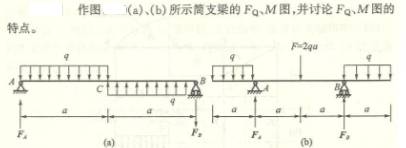
4.8
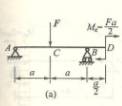
4.9
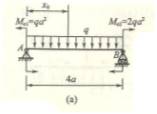
4.10
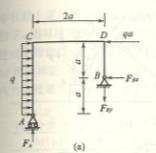
4.11
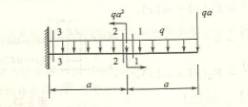
4.12
4.13
4.14
4.15
4.16
4.17
4.18
课后习题
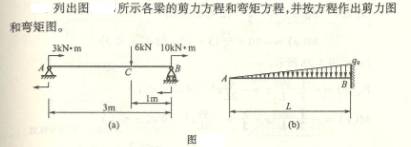
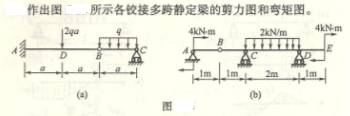
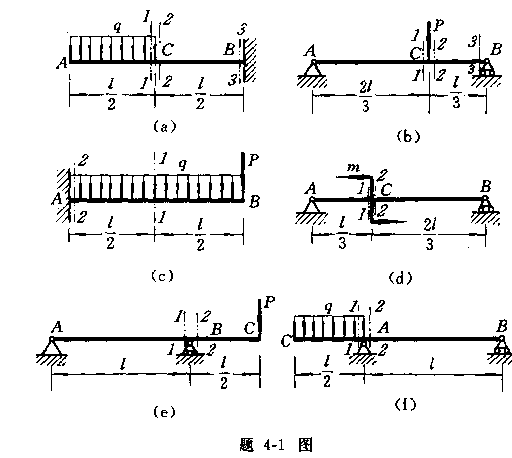
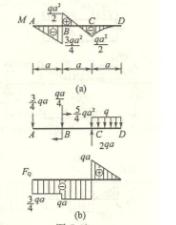
4-1
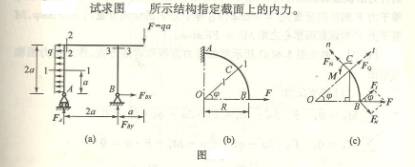
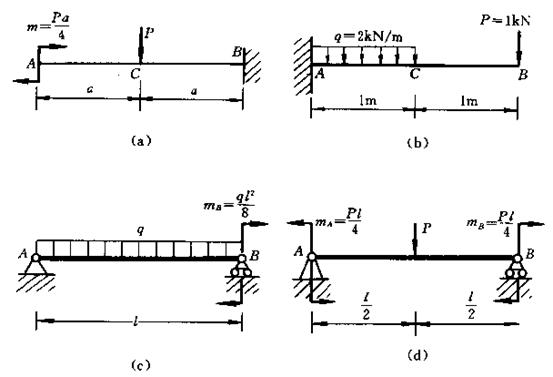
求下列各梁指定截面上的剪力Q和弯矩M。各截面无限趋近于梁上A、B、C等各点。
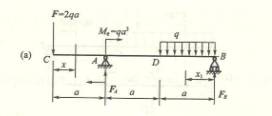
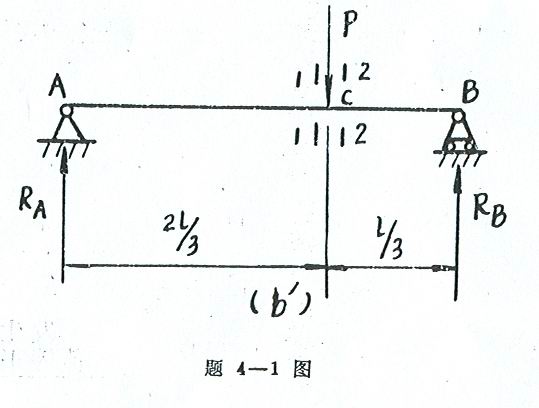
4-2 试列出下列各梁的剪力方程和弯矩方程，作剪力图和弯矩图，并求
和
。
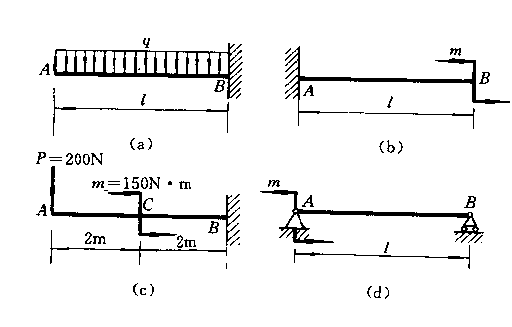
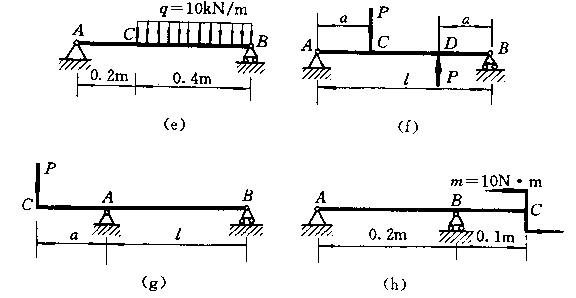
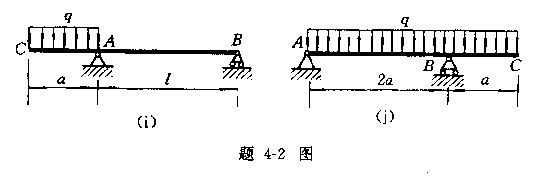
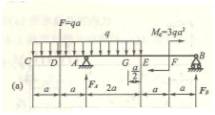
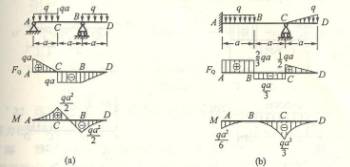
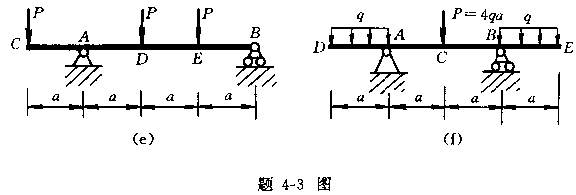
4-3 用叠加法作以下各梁的弯矩图。并求出
。
4-4
用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
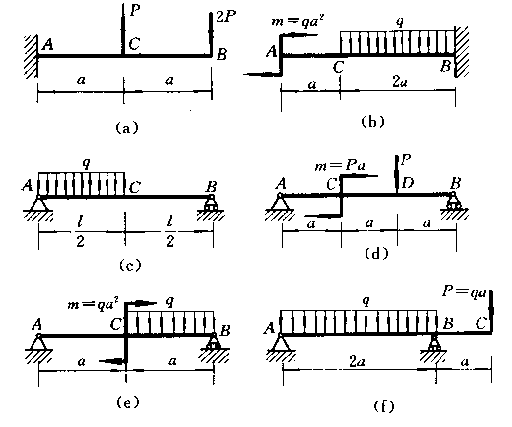
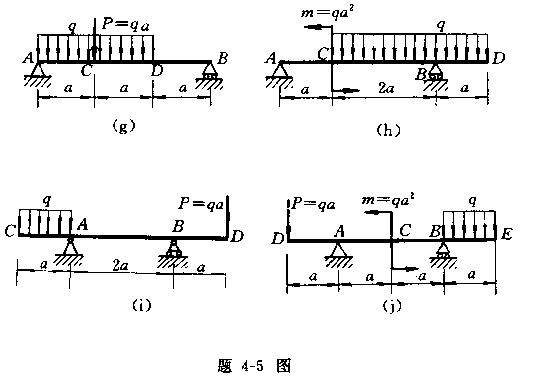
4-5
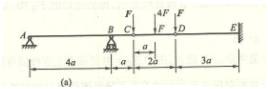
不列剪力方程和弯矩方程，作以下各梁的剪力图和弯矩图，并求出和。
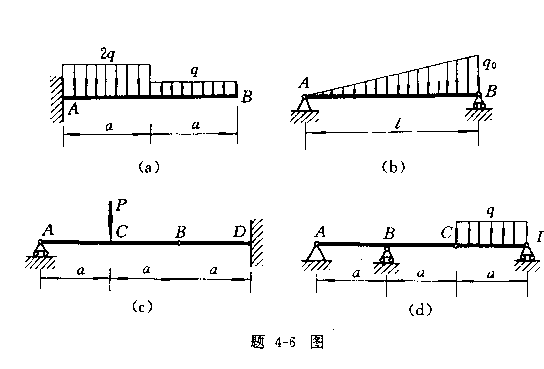
4-6
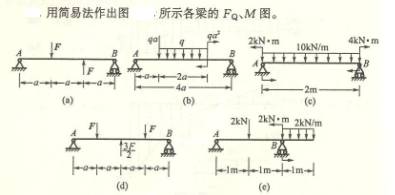
用合适的方法作下列各梁的剪力图和弯矩图。
4-7
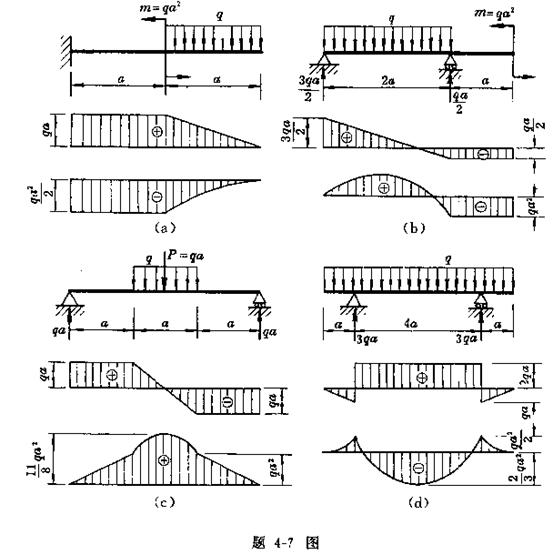
试根据载荷、剪力图和弯矩图之间的关系，检查下列各梁的剪力图和弯矩图是否正确，并对错误之处加以改正。
4-8
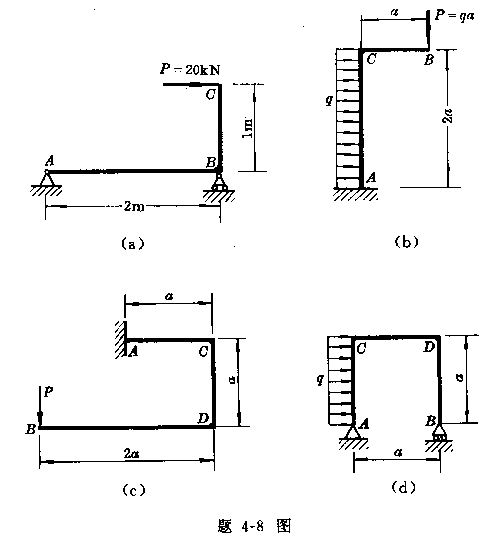
作下列构件的内力图。
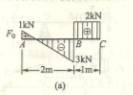
4-9
在梁上行走的小车二轮的轮压均为P ，如图所示。问小车行至何位置时梁内的弯矩最大？最大弯矩值是多少？设小车的轮
距为c，大梁的跨度为
。
参考答案
概念题答案
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
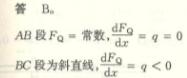
4.10
4.11
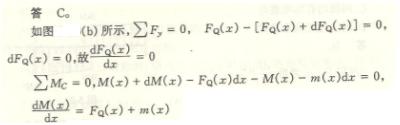
4.12
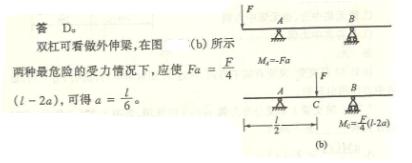
计算题答案
4.1
4.2
4.3
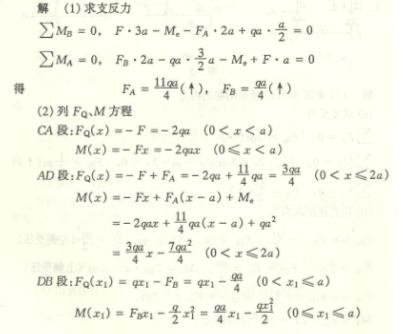
4.4
4.5
4.6
4.7
4.8
4.9
4.10
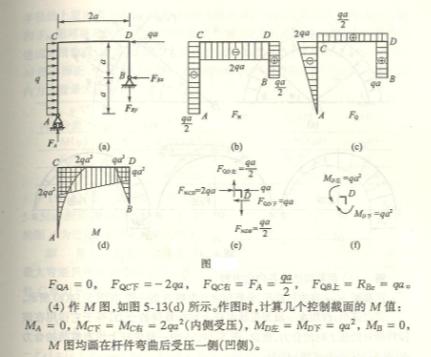
4.11
4.12
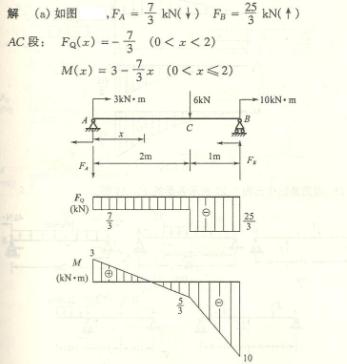
4.13
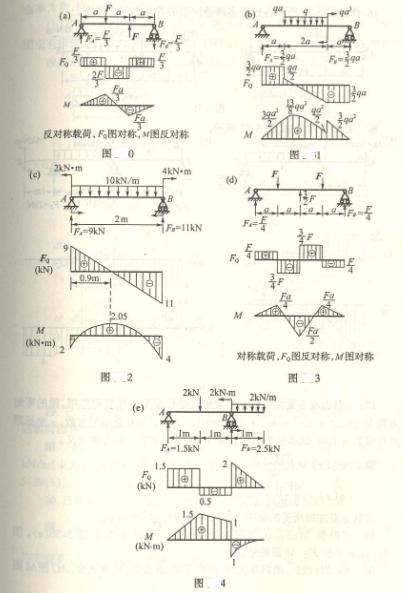
4.14
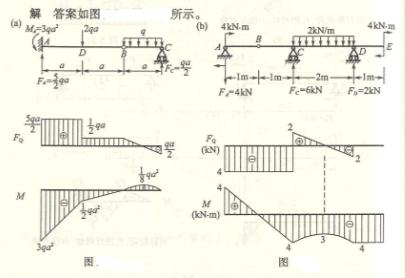
4.15
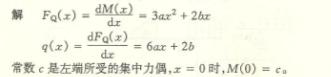
4.16
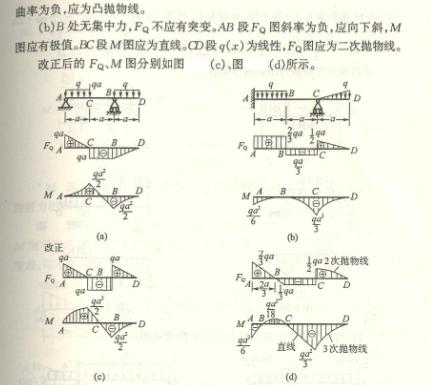
4.17
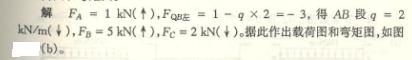
4.18
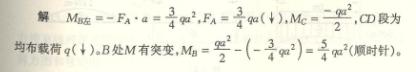
课后习题答案
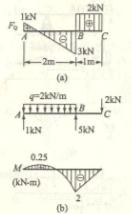
4-1 解：
题（b）
（1） 求支反力（见图
）
由
，
l-P
l=0 
=
由
，
（2）剪力
按计算剪力的规则
（3）弯矩
按计算弯矩的规则
其它各题的答案：
（a）
（c）
（d）
（e）
（f）
4-2 解：题c
(1)
剪力和弯矩方程 以左端A为原点，任一截面距左端的距离为x（图
）\
剪力方程:
弯矩方程:
(2 )剪力图与弯矩图
按上述剪力方程和弯矩方程绘剪力图和弯矩图
（3）
与值 由及得
=200N
=950
题（f）
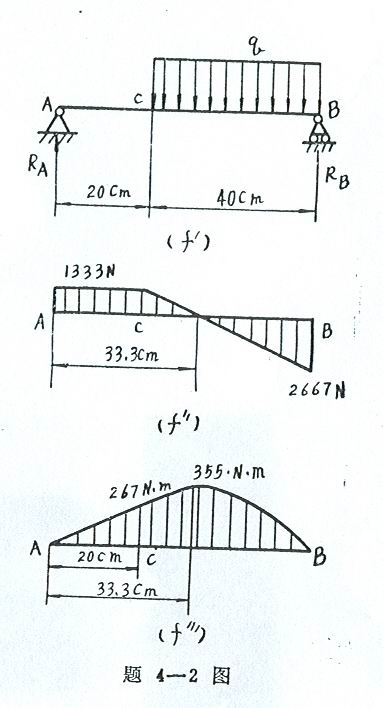
（1） 求支反力（见图
）
由
，
600-1004040=0
=
由
，q4020-
60=0
=
校核：
+=2667+1333=4000N=q40=10040 所以支反力计算正确
（2）剪力和弯矩方程
以左端为原点，任一截面距左端的距离为x，
则得剪力方程 ：
弯矩方程
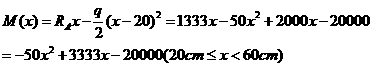
（2） 剪力图和弯矩图
按上述剪力及弯矩方程绘出图
及
所示的剪力图和弯矩图所示剪力图和弯矩图.
图中最大弯矩的截面位置可由
，即剪力
的条件求得
Q（x）=3333-100x=0
x=
（4）及
由及得
=2667N
，=355
其他各题的答案：
（a）=ql =
（b）
（d）
（e）
（g）
（h）
（i）
（j）
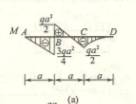
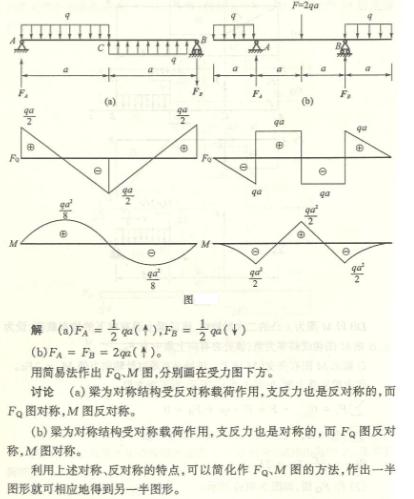
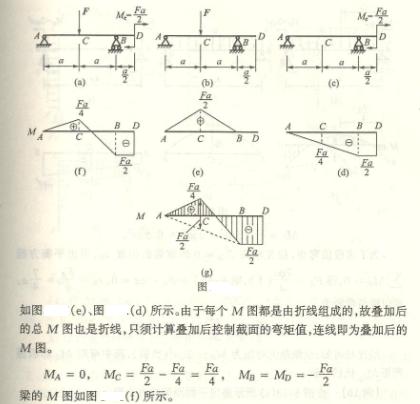
4-3 解：题c
分别作
、q单独作用时的弯矩图（图、），然后将此二图叠加得总的弯矩图
。由可知
题（）
分别作P和q单独作用时的弯矩图（图、
），然后将此二图叠加得总的弯矩图
。由可知
其他各题答案为：
（a）
（b）
（d）（e）
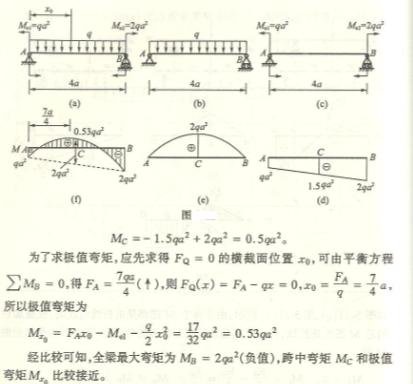
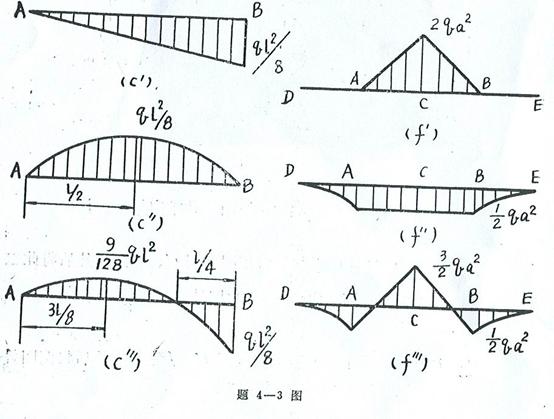
4-5 解：题（d）
（1） 求支反力（图
）
由，
=
由
Pa-Pa-
=0
=0
校核 +=P+0=P
满足
计算正确
（2） 绘剪力图及弯矩图如图
、
所示
（3） 及
其他各题答案：
（a）=2P,|
=3 Pa
(b) =2qa,|=q
(c) =
ql, =
q
4-6 解:题(a)
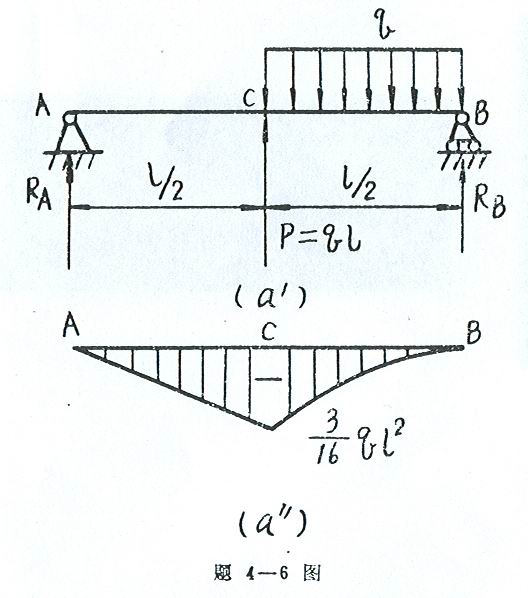
(1) 求支反力(图
)
由
=0，
×l-q×
×
+ql×=0
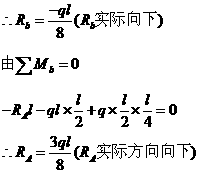
校核
（2）绘弯矩图 如
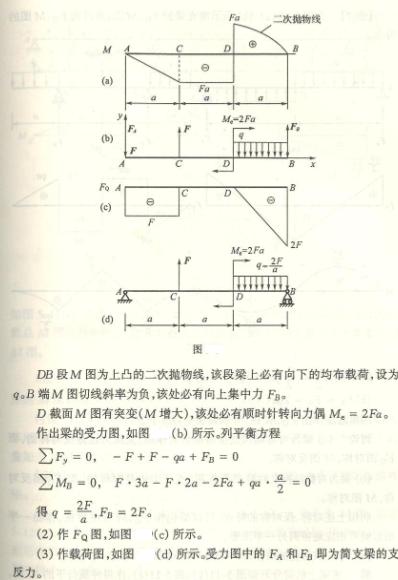
4-7 解：题（b）
此梁为带中间绞的静定梁。求解时可将梁AB段视为中点受集中力P的简支梁，梁BD段视为在悬臂端受集中力
作用的悬
臂梁，值可由AB梁的平衡条件求得 =
=
。由此绘出两段梁的弯矩图分别如图
、
所示。
由图、知|=
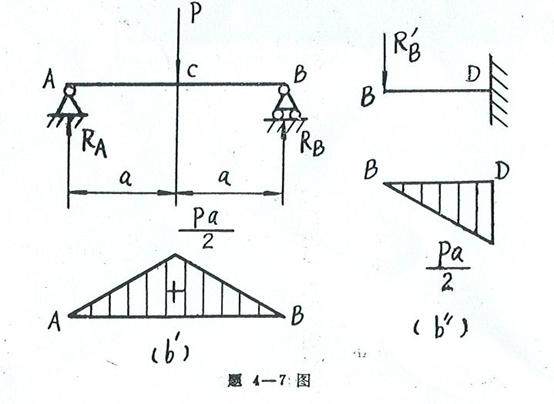
题(c)
(1) 求支反力（图
）
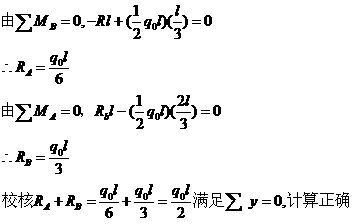
（2） 弯矩方程 以A为截面位置的坐标x的弯矩方程为：
（3）弯矩图如图
所示。
（4）|=0.06415
其他各题答案
（a）|= 
(d)
|=
4-9 答：
或
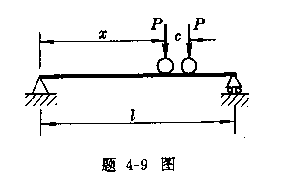
