第六章 弯曲变形 静不定梁习题
概念题
6.1
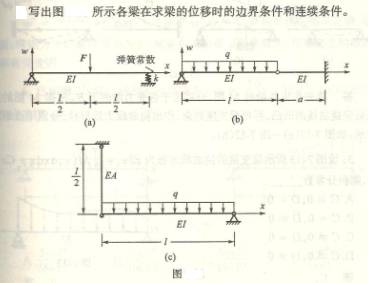
6.2
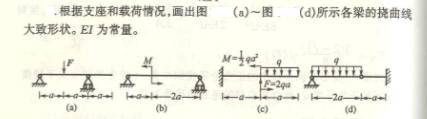
6.3
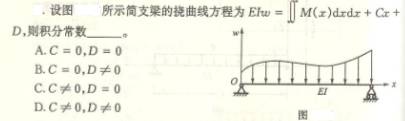
6.4
6.5
6.6
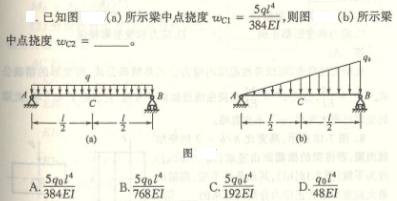
6.7
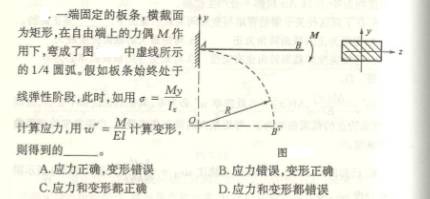
6.8
6.9
6.10
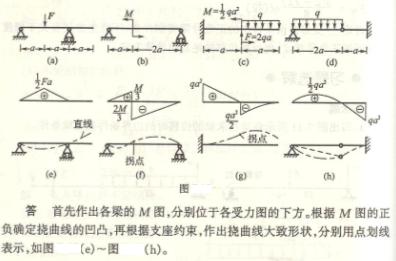
在下面关于梁、挠度和转角的讨论中，（）是错误的
A. 挠度的一阶导数等于转角
B. 可以用简支梁的跨度中点的挠度代替最大的挠度
C. 弯矩为零的一段梁上各界面的转角相等，挠度不一定相等
D. 挠度最大的截面和转角不一定为零
计算题
6.1
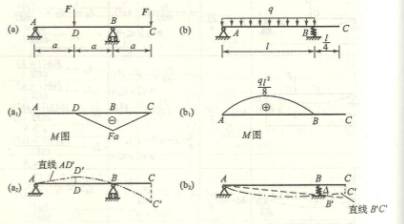
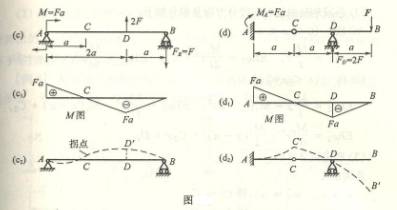
6.2
6.3
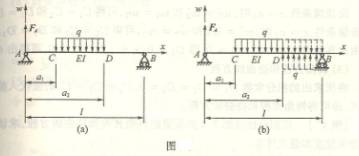
6.4
6.5
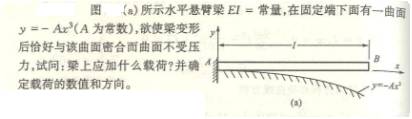
6.6
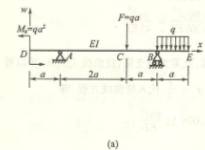
6.7
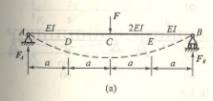
6.8
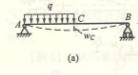
6.9
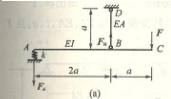
6.10
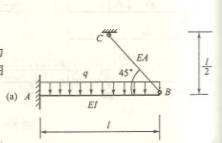
6.11
6.12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.20
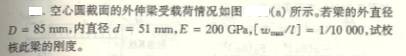
6.21
6.22
6.23
课后习题
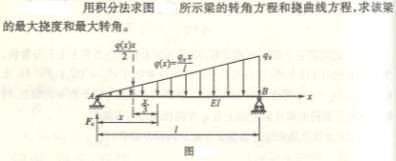
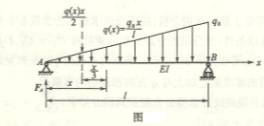
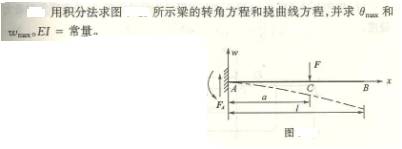
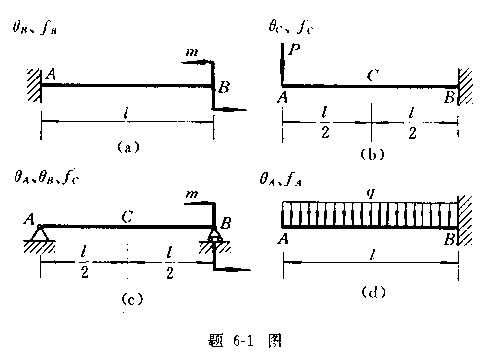
6—1 用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。已知抗弯刚度EI为常数。
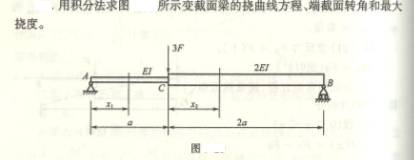
6-2、用积分法求以下各梁的转角方程、挠曲线方程以及指定的转角和挠度。已知抗弯刚度EI为常数。
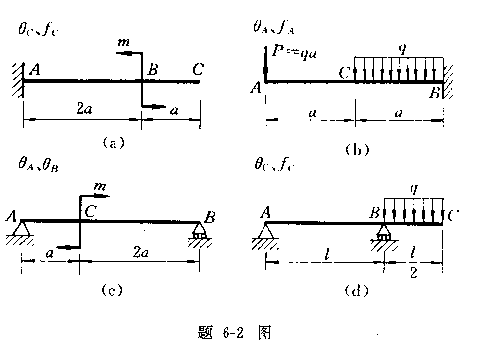
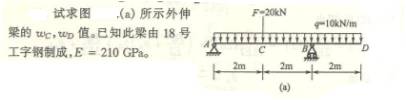
6-3、用叠加法求图示各梁中指定截面的挠度和转角。已知梁的抗弯刚读EI为常数。
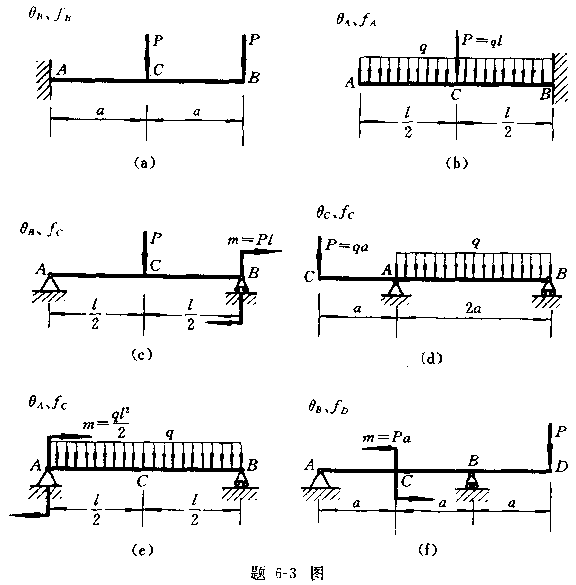
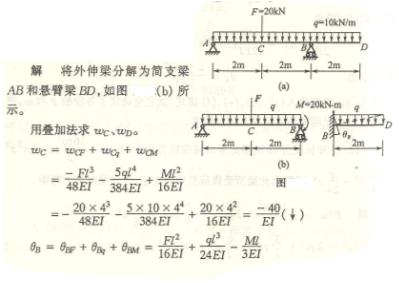
6-4阶梯形悬臂梁如图所示，AC段的惯性矩为CB段的二倍。用积分法求B端的转角以及挠度。
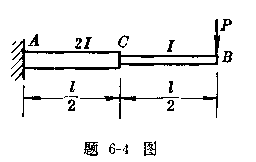
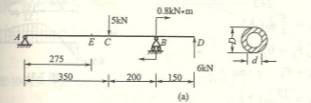
6-5一齿轮轴受力如图所示。已知：a=
]
=0.005rad。近似的设全轴的直径均为d=
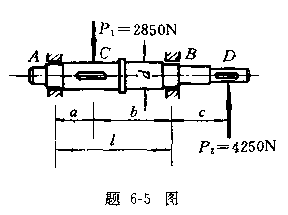
回答：
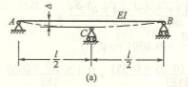
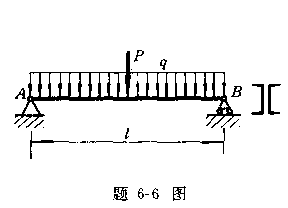
6-6一跨度为
]=160Ma,梁的许
用挠度[
]=
。试选择槽钢的号码，并校核其刚度。梁的自重忽略不计。
6-7两端简支的输气管道，外径D=
=
试确定管道的最大跨度。
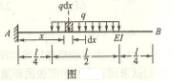
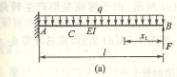
6-8 
，求梁所能承受的布满全梁的
最大均布载荷q。
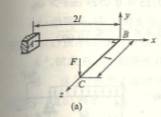
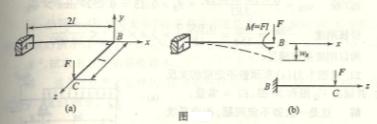
6-9一直角拐如图所示，AB段横截面为圆形，BC
段为矩形，A段固定，B段为滑动轴承。C端作用一集中力P=60N。有关尺寸如
图所示。材料的弹性模量E=210Gpa,剪切弹性模量G=0.4E。试求C端的挠度。
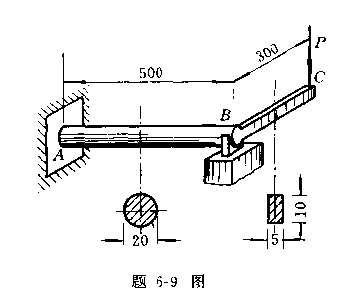
提示：由于A端固定，B端为滑动轴承，所以BC杆可饶AB杆的轴线转动。C端挠度由二部分组成；（1）把BC杆当作悬臂梁，受
集中力P作用于C端产生的挠度
，
；（2）AB杆受扭转在C锻又产生了挠度
，
。最后，可得
C端的挠度
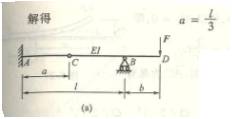
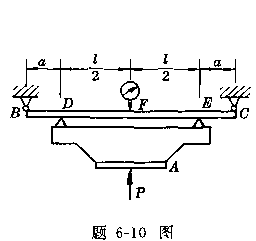
6-10、以弹性元件作为测力装置的实验如图所示，通过测量BC梁中点的挠度来确定卡头A处作用的力P，已知
,
梁截面宽b=
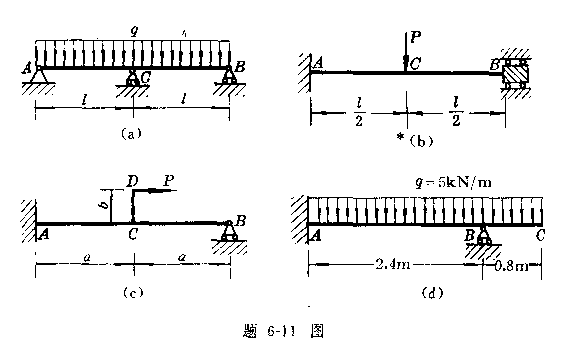
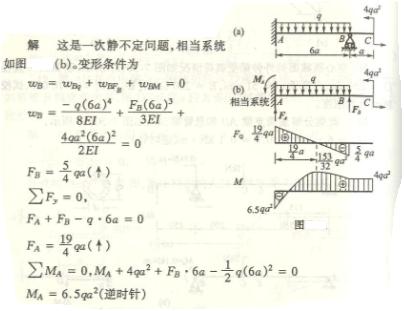
6-11试求以下各梁的支反力，并做弯矩图。
由图可见有三个支反力，但在平面能够力系中，只可列出二个静力平衡方程，可知此梁是静不定梁问题。
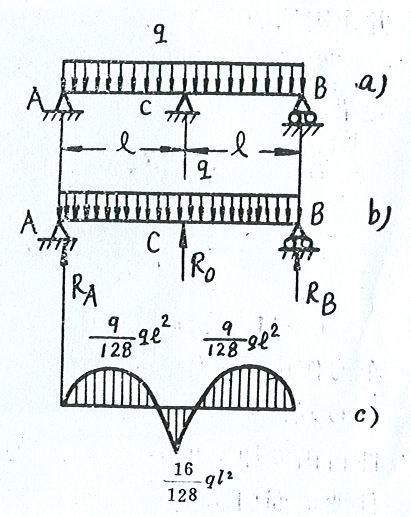
（1）选取静定基，建立变形条件
假想解除多余约束C，选取静定基如图（b），变形条件为
（2）计算变形
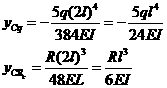
（3）
建立补充方程，解出多余反力
利用变形条件，可得补充方程
算出中间支座的反力，
（4） 由平衡条件求其他支座反力
因为此梁的载荷和结构有对称性，可知
（5） 作弯矩图如图c) 
在中间支座处
6-12加热炉内的水管横梁，支持在三个支点上，承受纵管传来的钢锭载荷。求A、B、C处的反力。并作横梁的弯矩图。
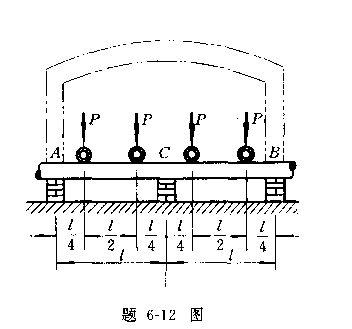
提示：横管简化成三支点的静不定梁。
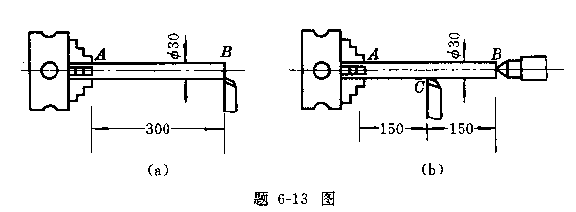
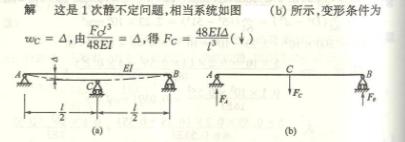
6-13在车床加工工件，已知工件的弹性模量E=220GP
a,试问（1）按图（a）方式加工时，因工件而引起的直径误差是多少？
（2）如在工件自由端加上顶尖 后，按车刀行至工作中点时考虑（b），这时因工件变形而引起的直径误差又是多少？（3）二
者误差的百分比如何？
提示：（a）情形可简化成在右端作用一集中力P的静定是悬臂梁，（b）情形可简化成左端固定右端简支的静不定梁，在中点作
用一集中力Ｐ。计算直径的误差时，应是所求得挠度的二倍。
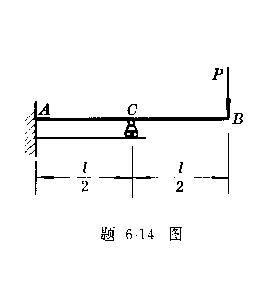
６－１4、悬臂梁ＡＢ因强度和刚度不足，用同材料同截面的一根短梁ＡＣ加固，如图所示。问（１）支座Ｃ处的反力
为多
少？（２）梁ＡＢ的最大弯矩和最大挠度要比没有梁
AＣ支撑时减少多少？
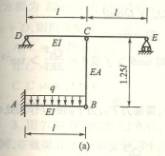
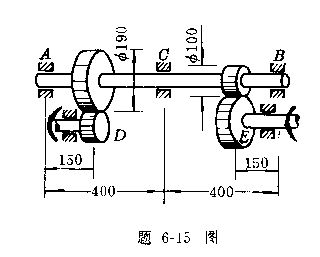
6-15、图示一铣床齿轮轴AB，已知传动功率
，转速n=230rpm,D轮为主动轮。若仅考虑齿轮切向力的影响，试求此
轴的弯矩图。
参考答案
概念题答案
6.1
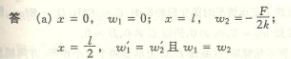
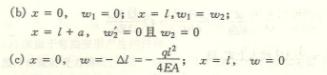
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
B（提示：挠曲线无拐点时才可以）
计算题答案
6.1
6.2
6.3
6.4
6.5
6.6
6.7
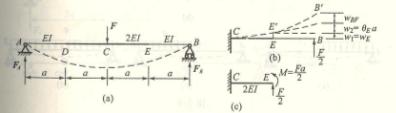
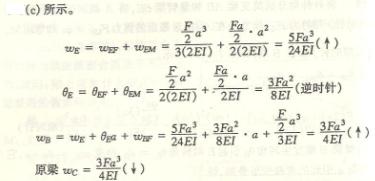
6.8
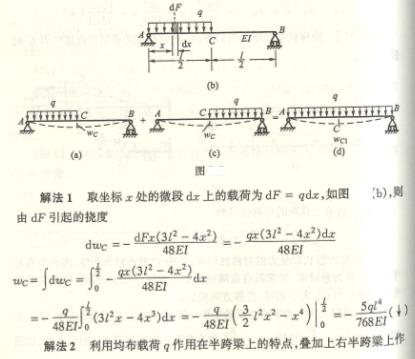
6.9
6.10
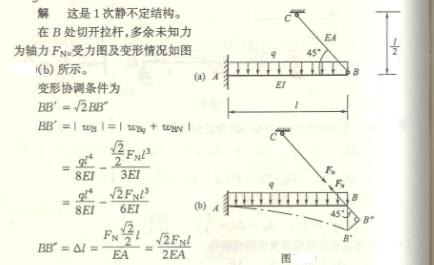
6.11
6.12
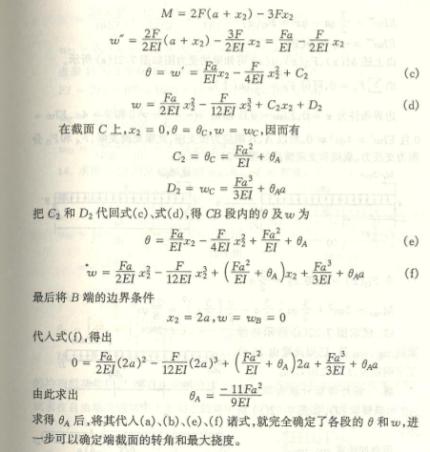
6.13
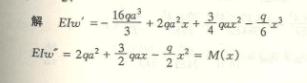
6.14
6.15
6.16
6.17
6.18
6.19
6.20
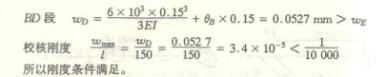
6.21
6.22
6.23
课后习题答案
6—1 解：(a)
挠曲线微分方程为：
积分得：
（1）
（2）
在固定端A，转角和挠度均应等于零，即：
当x=0时， 
；
把边界条件代入（1），（2）得
C=0
D=0
再将所得积分常数
（3）
（4）
求B点处转角和挠度
x=l时代入（3），（4）
（b）任意截面上的弯矩为： 
挠曲线的微分方程： 
积分得 
(1)
(2)在固定端B
当x=0时
将边界条件代入（1）、（2）中，得：
C=D=0
再将所得积分常数C和D代回（1）、（2）式，得转角方程和挠曲线方程
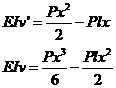
以截面C的横坐标x=l/2代入以上两式，得截面C的转角和挠度分别为
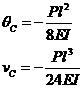
(c)求支座反力：
=0
选取如图坐标，任意截面上的弯矩为：
挠曲线的微分方程为：
积分得：
（1）
（2）
铰支座上的挠度等于零，故
x=0时
因为梁上的外力和边界条件都对跨度中点对称，挠曲线也对该点对称。因此，在跨度中点，挠曲线切线的斜率
截面的转角都应等于零，即
x=
时
=0
分别代入（1）、（2）式，得
，D=0
以上两式代入（1）（2）得
当x=0时，
当x=l/2时，
6-2解：AC段，
（d）、
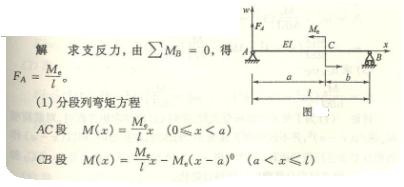
解：取坐标系如图。
（1）、求支坐反力、列弯矩方程
支座反力，
AB段，
BC段，
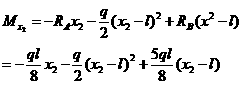
(2)列梁挠曲线近似微分方程并积分
AB段，
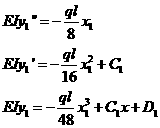
BC段，
（3）确定积分常数
利用边界条件：
处，
，代入上面
式中，得
，
处，，再代入式中，得
处，
，由
和
式可得
。
处，
，代入
式中，得
（4）转角方程和挠度方程
AB段，
BC段，
最后指出，列弯矩方程时，
不变，
也可取截面右侧的载荷列出，
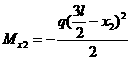，这样可使计算大为简化。
6-3、解：（a）计算转角
左、右集中力P分别为
和
表示集中力作用下引起的转角，
集中力作用下引起的转角，
所以 
（1） 计算挠度
集中力作用下引起的挠度，
集中力作用下引起的挠度
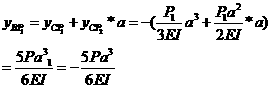
所以
答（b）
，
（c）(1) 计算转角
力偶
作用下引起的转角
力P作用下引起的转角
所以
（2）、计算挠度
力偶 作用下引起的挠度
力P作用下引起的转角
所以
回答
(d )
,
(e) 
,
(f) 解答：
（1计算转角力P作用下引用的转角
力偶作用下引起的转角
所以 
（2计算挠度
力P作用下引起的挠度
力偶作用下引起的挠度
所以 
6-5回答：
6-6解：（1） 选择截面
采用迭加法可求得最大弯矩
由正应力强度条件可得
（2） 校核刚度
采用迭加法可求得最大挠度
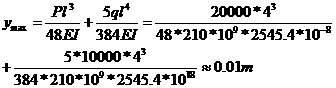
计算可知
，此钢梁的刚度够。
6-7 答：
6-8 答：
6-9提示：由于A端固定，B端为滑动轴承，所以BC杆可饶AB杆的轴线转动。C端挠度由二部分组成；（1）把BC杆当作悬臂梁，受
集中力P作用于C端产生的挠度，；（2）AB杆受扭转在C锻又产生了挠度，。最后，可得
C端的挠度
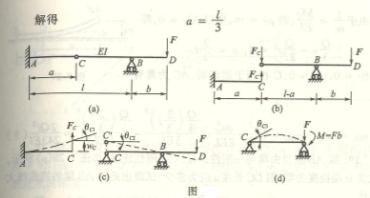
6-11答：（b） 
提示：题（c）在固定端处，除有反力偶
及竖直反力
外，还有水平反力
，此梁是一次静不定梁。可以解除支
座B，选择反力
作多余反力，建立补充方程求解。
答：
答（d）
，在固定端。
6-12答：
在距离两端的
处。
6-13答：（１）
二者误差百分比为２.７３％
６－１4解：（1）计算约束反力
根据在加固处两个悬臂梁的挠度相等这个变形条件，来计算约束反力。即
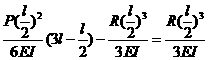
可得
（2） 比较最大弯矩
没有加固梁时，
有加固时，
比较可知，梁AB加固后，最大弯矩可减少一半。
（3） 比较最大挠度
没有加固梁时，
有加固时，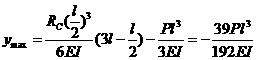
经加固后，梁AB在右端的最大挠度要减少
6-15解：
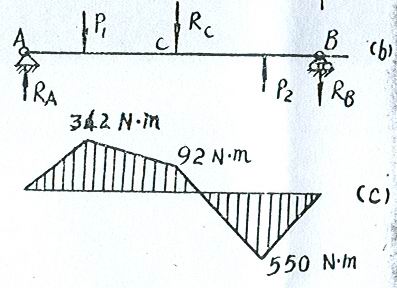
（1） 计算AB轴上的外力
AB轴上的外力偶矩
作用于AB轴的左右齿轮上的切向力为
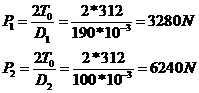
（2） 求AB轴上的约束反力
AB轴是一次静不定梁，取静定基如图（b）,变形条件为
而
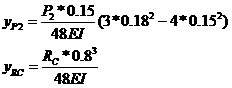
代入有关数据，再代回变形条件中，可得
由平衡条件，
（3） 作弯矩图
AB轴的弯矩图如图（c）
。