第三章 习题

一、简答

1.什么是基本体？如何分类？

2.简述圆柱的投影特性

3. 在圆锥表面取点有几种方法？简述素线法的作图原理。

4. 简述用纬圆法圆在圆锥表面取点的作图原理。

5. 什么是平面体？什么是曲面体？各举两个例子说明。

6. 简述判断平面体表面上的点投影可见性的方法。

二、填空

7．平面立体棱线上的点称为 点，表面上的点称为 点。

8. 回转体投影外形线上的点称为 点，表面上的点称为 点。

9．用过圆锥顶的直线在其表面上取点的方法，叫做 。

10．用纬圆法求圆锥表面上的点时，纬圆的直径大小与纬圆的圆心到锥顶的距离 。距离小，则直径 ，反之，直径 。

11．当圆柱体的轴线垂直于水平面时，圆柱面的水平投影具有 ，其形状是 。

12. 在圆柱表面所作的直线一定与圆柱轴线 。

13. 在圆锥表面所作的直线一定是过 的。

14.基本体有两种，分别是 体和 体。

15.当圆锥的轴线垂直于H面时，圆锥底面的水平投影为 形，其正面与侧面投影是与相应轴线 的 ，

16. 当圆锥的正面投影为圆时，锥顶的正面投影位置在该圆的 。

17. 基本体三面投影之间的对应关系是：正面投影与水平投影 ；

正面投影与侧面投影 ；侧面投影与水平投影 。

18. 棱柱体的上下两个底面是互相 且 的。

三、判断（对T, 错F）

19. 圆锥面的三个投影都没有积聚性。

20. 圆球表面也有直线。

21. 圆球的三个投影一定是直径相等的圆

22. 构成一个棱柱体的棱线数与棱面数是相等的。

23. 圆柱体的轴线一定是与水平面垂直的。

四、选择(单选、多选)

24．铅垂圆锥面上锥顶的水平投影位于（ ）。

A. 圆心B. 水平直径的左端点 C. 竖直直径的后端点 D. 水平直径的右端点

25. 棱线为铅垂线的棱柱顶面上的点，其水平投影是（ ）。

A. 可见的 B. 不可见的 C. 不确定

26. 轴线为正垂线的圆柱体最右外形线上的点，其侧面投影位于（ ）， 而且是（）

A. 轴线上，可见B. 投影外形线上，不可见C. 轴线上，不可见D. 均不确定

27. 因为圆锥的三个投影都没有积聚性，所以当

A. 轴线垂直H面时，圆锥面上点的水平投影都可见

B. 轴线垂直V面时，圆锥面上点的正面投影均可见

C. 轴线垂直V面时，圆锥底面上点的正面投影都可见。

D. 轴线垂直H面时，圆锥底面上点的水平投影都不可见。

28. 当棱锥的底面与水平面平行时，该面的水平投影具有（ ），且该底面上点水平的投影（ ）。

A. 真实性，可见B. 积聚性，可见 C. 类似性，不可见 D. 真实性，不可见

五、看图分析并回答问题：

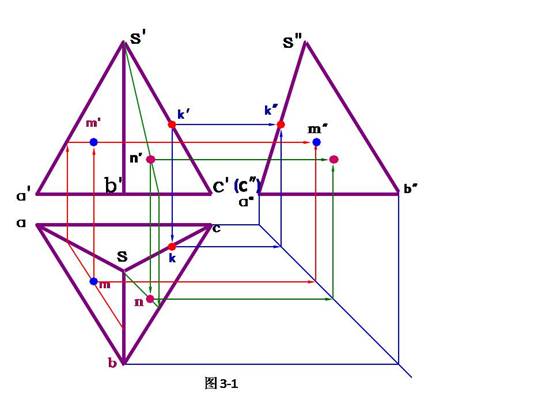
29.找出图3-1中的特殊点和一般点，并指出它们所在的位置。

30.判断点N的侧面投影可见性及其在图上的表示方法。

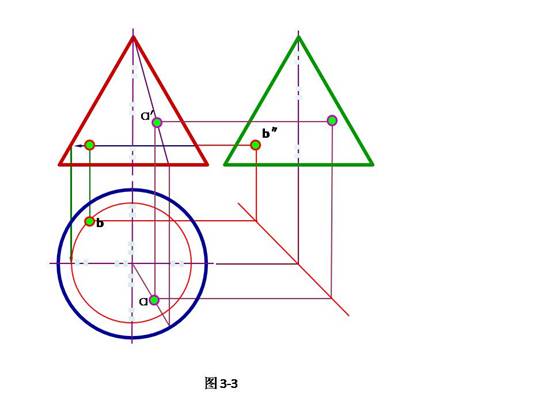
六、 如图3-3所示，回答下列问题：

31. 圆锥表面上的点A，B的取点方法是什么？

32. A、B两点是什么类型的点？

33. 若已知圆锥表面上点B的侧面投影，按图3-3所示方法写出求该点水平投影和正面投影的作图步骤，并判别可见性。

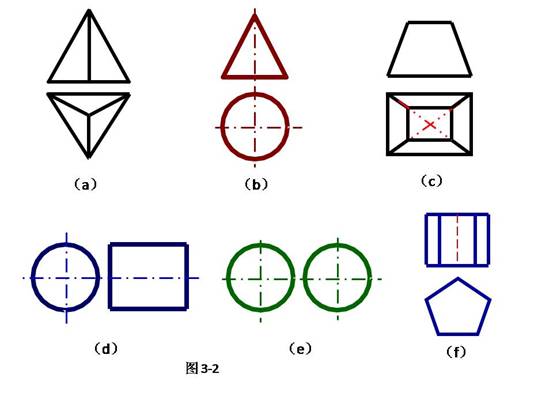
七、看图3-2回答问题

34. 表面具有积聚性投影特性的立体有哪些？并指出它们相对哪个投影面具有积聚性。

35.图3-2(f)中的正面投影的虚线表示的含义是什么？

36.将图中所给立体分类

参考答案

一、简答

1.把工程上常用的单一几何形体称为基本体。基本体分为两类，一类是平面体，另一类是曲面体

2.当圆柱的轴线与某个投影面垂直时，圆柱在该投影面上的投影具有积聚性，其投影为一个与圆柱直径大小相等的圆。另外两个投影为大小相等的矩形。

3. 在圆锥表面取点有两种方法，纬圆法和素线法。

素线法的作图原理：过点及锥顶作直线，即为圆锥表面的素线，求出该素线的投影，而点在圆锥表面上，也在圆锥表面的一条素线上。

4. 纬圆法的作图原理是：过已知点作与圆锥底面的平行圆，在与之平行的投影面上投影反映实形，另外两个投影积聚为与投影轴平行的直线，点即为该辅助圆上的的点。辅助圆的直径等于积聚性投影与圆锥投影外形线相交处的长度。

5. 完全由平面所围成的立体称为平面立体。如四棱柱，三棱锥。

完全由曲面或曲面与平面所围成的立体称为曲面体。如圆球，圆柱。

6. 平面体表面上的点在某个投影面上的投影是否可见，首先应判断该点所在的平面在该投影面上是否可见，如平面的投影可见，则该面上的点投影也可见，反之，则为不可见。

二、

7．特殊点，一般点 8. 特殊点，一般点 9.素线法 10.有关，小，大

11. 积聚性，圆 12. 平行 13. 圆锥的锥顶 14. 平面，曲面

15. 圆，平行，直线 16. 圆心 17. 长对正，高平齐，宽相等18. 平行，相等

三、19. T 20. F 21. T 22. T 23. F

四、24．A 25. A. 26. C 27. A,B,D 28. D

五、

29. 点K是特殊点，位于棱线SC上。点M、N是一般点，分别位于三角形棱面SAB和SBC上。

30. 因为N点所在的平面的侧面投影不可见，所以点N的侧面投影不可见，在图上应表示为（n”）。

六、

31. 其中点A的取点方法是素线法，点B的取点方法是纬圆法。

32. 点A、点B均为圆锥表面上的一般点。

33. 作图步骤：1）过b”X轴平行线，与圆锥轮廓线相交；

2）以圆锥水平投影圆的圆心为圆心，正面投影轴线到轮廓线的距离为半径，在水平投影面上画圆；

3）作45°辅助线，根据点B的侧面投影可见，且在后半圆锥面上，将点的水平投影确定，为可见，

4）求出点的正面投影，根据上述分析，B点的正面投影不可见，表示为（b”）。

七、

34.（d）（f）的立体的投影具有积聚性。其中（d）的轴线与正面垂直，所以正面投影具有积聚性，而（f）的轴线与水平面垂直，所以水平投影具有积聚性。

35.表示五棱柱的最后一条棱线的正面投影不可见。按规定，不可见轮廓线的投影画虚线。

36.分为两类：平面立体包括：三棱锥、四棱台和五棱柱

曲面立体包括：圆锥、圆柱和圆球