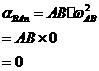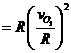第九章 习题
概念题:
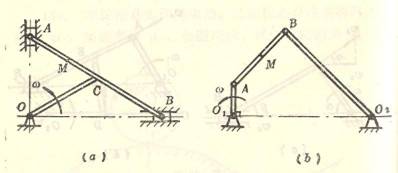
9.1

9.3 9.2
![]()

9.4

9.5

9.6
![]()
9.7
![]()
9.8
![]()
9.9
![]()
9.10

9.11

9.12
![]()
9.13

计算题:
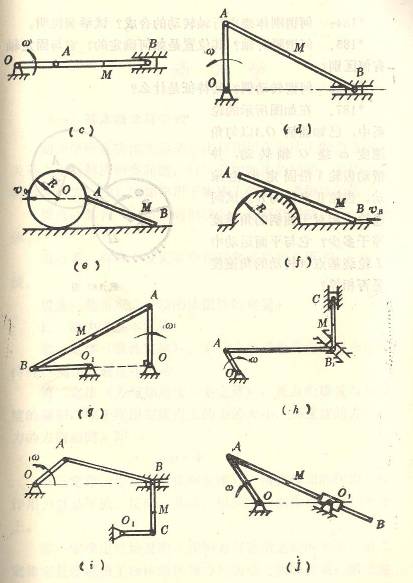
9.1

9.2

9.3

9.4
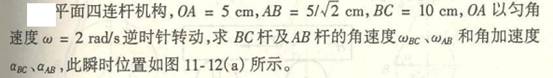
9.5

9.6

9.7
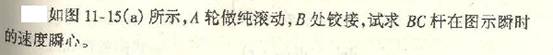
9.8

9.9

9.10

9.11

9.12

9.13

9.14

9.15


9.17 9.16

9.18


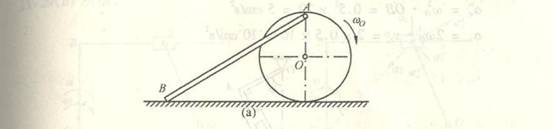
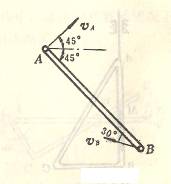
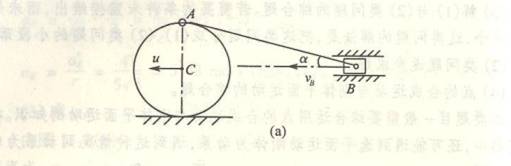
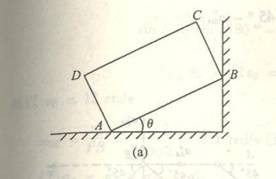
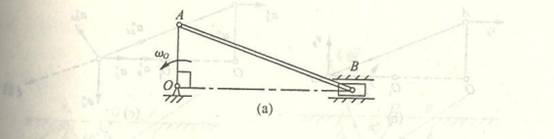
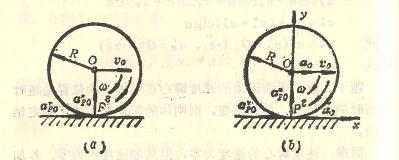
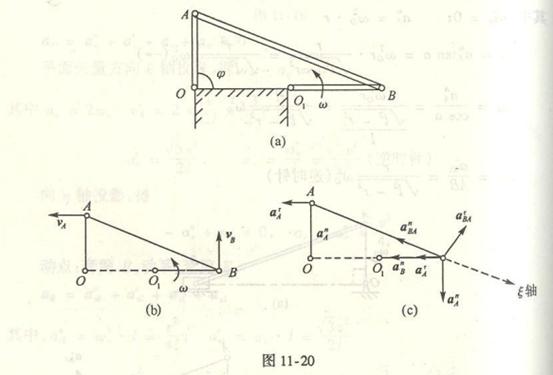
4-1椭圆规尺AB由曲柄OC带动,曲柄以匀角速度![]() =2rad/s绕O轴转动。已知OC=BC=AC=12cm;求当
=2rad/s绕O轴转动。已知OC=BC=AC=12cm;求当![]() =
=![]() 时A点与B点的速
时A点与B点的速
度。
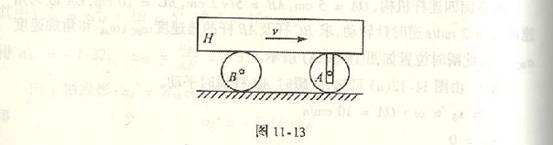
4-2履带拖拉机以速度![]() 沿直线道路行驶(不滑动),已知前后轮半径为R。求履带上
沿直线道路行驶(不滑动),已知前后轮半径为R。求履带上![]() 、
、![]() 、
、![]() 、
、![]() 四点的速度。
四点的速度。

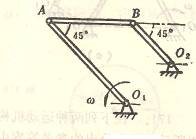
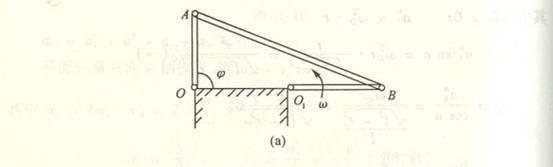
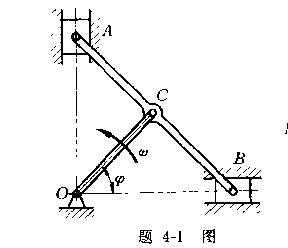
4-3偏置曲柄连杆机构,曲柄以匀角速度 ![]() =0.5rad/s绕O轴转动。如OA =40cm,AB=200cm,OC=20cm。求当曲柄在两水平和铅
=0.5rad/s绕O轴转动。如OA =40cm,AB=200cm,OC=20cm。求当曲柄在两水平和铅
直位置时滑块B的速度。
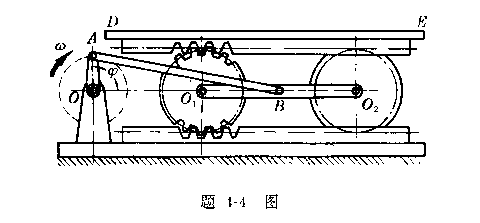
4-4图示为曲柄连杆机构带动平台DE作往复直线运动的机构。曲柄作匀角速度转动,其角速度![]() =2
=2![]() rad/s。OA=10cm,
rad/s。OA=10cm,
AB=30cm,齿轮![]() ,
,![]() 上下均与齿条啮合。求当
上下均与齿条啮合。求当![]() =
=![]() 时平台DE的速度和加速度。
时平台DE的速度和加速度。
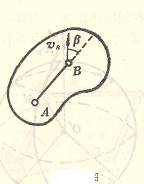
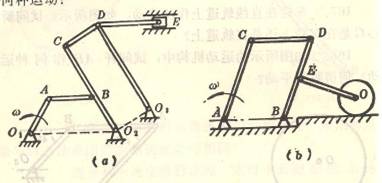
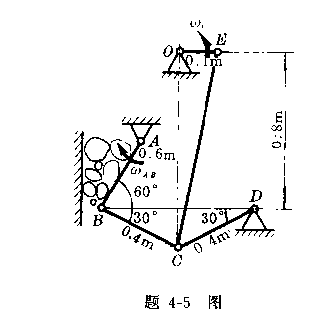
4-5腭式破碎机的简图如图所示。OE,EC,CD,DO是一四连杆机构,曲柄OE绕O轴以![]() 匀速转动,通过连杆EC带动CD杆绕D
匀速转动,通过连杆EC带动CD杆绕D
点摆动。DC、CB、BA、AD又是一四连杆机构,CD杆通过连杆CB带动腭板AB绕A点来回摆动,把矿石压碎。已知![]() =10rad/s;
=10rad/s;
各杆长度及其尺寸如图所示。长度单位为m。求图示位置时腭板摆动的角速度![]() 。
。
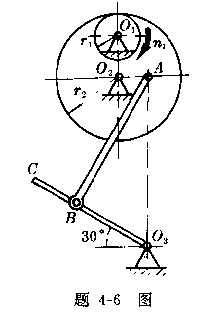
4-6人力打稻机的传动机构如图所示。踏板![]() 通过连杆AB带动大齿轮绕
通过连杆AB带动大齿轮绕![]() 轴转动,大齿轮又带动小齿轮转动,小齿轮与打稻
轴转动,大齿轮又带动小齿轮转动,小齿轮与打稻
机滚筒安装在同一轴上。已知![]() =4cm,
=4cm,![]() =6cm,
=6cm,![]() =20cm,
=20cm,![]() =30cm。若滚筒转速
=30cm。若滚筒转速![]() =120r/min;求图示位置(
=120r/min;求图示位置(![]()
![]() AB,
AB,
![]()
![]()
![]()
![]() ,
,![]() 水平,A在
水平,A在![]() 同一直线上,
同一直线上,![]() =
=![]() )踏板上的C点速度。
)踏板上的C点速度。
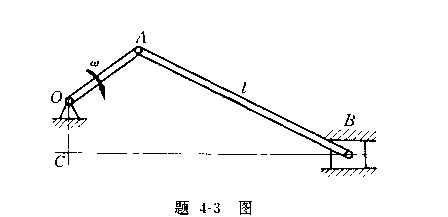
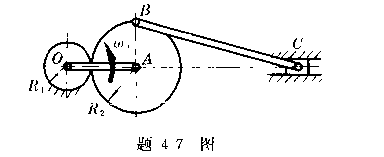
4-7曲柄OA=30cm,以角速度![]() =0.5rad/s绕O轴转动。半径
=0.5rad/s绕O轴转动。半径![]() =20cm的齿轮在半径
=20cm的齿轮在半径![]() =10cm的固定齿轮上滚动而不是滑动,并
=10cm的固定齿轮上滚动而不是滑动,并
带动与其连接的连杆BC,BC=20![]() cm。当半径AB垂直于曲柄OA时,求连杆的角速度及B点与C点的速度。
cm。当半径AB垂直于曲柄OA时,求连杆的角速度及B点与C点的速度。
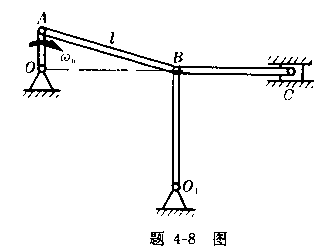
4-8求在如图所示的机构中,当曲柄OA与![]() 为铅垂时,B点与C点的速度与加速度。已知曲柄OA 以等角速度
为铅垂时,B点与C点的速度与加速度。已知曲柄OA 以等角速度![]() =5rad/
=5rad/![]() 转
转
动,并在此瞬时其角速度为![]() =10rad/s,OA=r=20cm,
=10rad/s,OA=r=20cm,![]() =100cm,AB=l=120cm,BC=100cm。
=100cm,AB=l=120cm,BC=100cm。
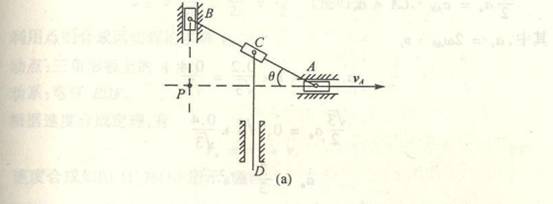
4-9由曲柄连杆机构OAB带动滑道作变角速度转动。OA=r=5,AB=BD=l=13cm,![]() =10rad/s。当曲柄在铅直位置时,滑道与水平
=10rad/s。当曲柄在铅直位置时,滑道与水平
成![]() 的夹角。求此瞬时摆杆
的夹角。求此瞬时摆杆 ![]() 的角速度及滑块D的速度。
的角速度及滑块D的速度。
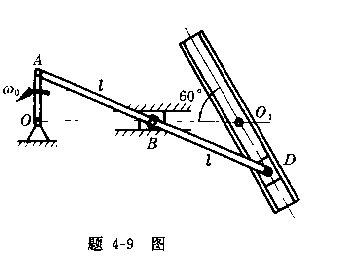
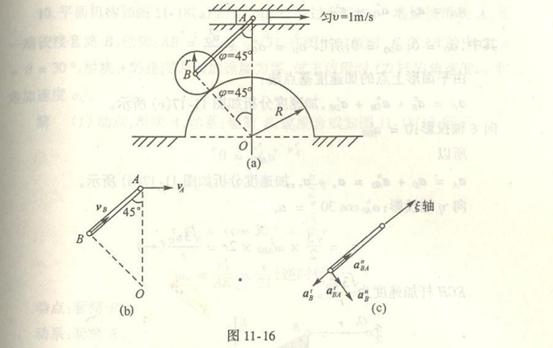
4-10冲床的曲柄四连杆机构如图所示,当曲柄OA作等角速度 ![]() 绕O轴转动时,连杆AB使杆B
绕O轴转动时,连杆AB使杆B![]() 绕
绕![]() 轴摆动,又通过连杆BC带
轴摆动,又通过连杆BC带
动滑块C上下运动。已知OA=r,AB=L,B![]() =BC=l,试求图示位置时滑块C 的速度。
=BC=l,试求图示位置时滑块C 的速度。
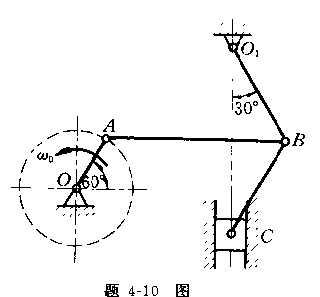
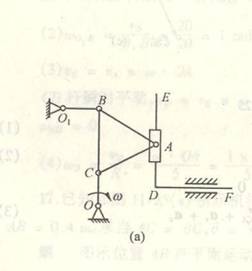
4-11已知小型锻压机的尺寸,OA=![]() B =10cm,EB=BD=AD=40cm。曲柄OA、
B =10cm,EB=BD=AD=40cm。曲柄OA、![]() B分别绕O、
B分别绕O、![]() 定轴转动,EBD是一根直的连
定轴转动,EBD是一根直的连
杆。在图示位置时,OA![]() AD,
AD,![]() B
B![]() ED,
ED,![]() D和OD分别为水平和铅直。当曲柄OA的转速n=120r/min时,求重锤F的速度。
D和OD分别为水平和铅直。当曲柄OA的转速n=120r/min时,求重锤F的速度。
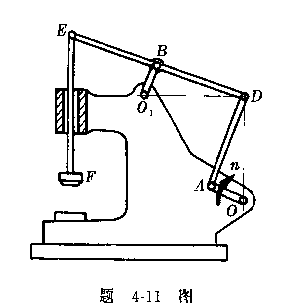
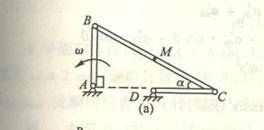
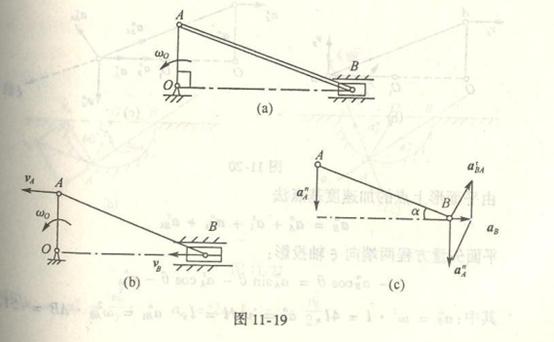
4-12在四连杆机构中,曲柄OA=r,以匀角速度![]() 转动,连杆AB =4r。求在图示位置时摇杆
转动,连杆AB =4r。求在图示位置时摇杆![]() B的角速度与角加速度,并求连杆
B的角速度与角加速度,并求连杆
中点M的加速度。
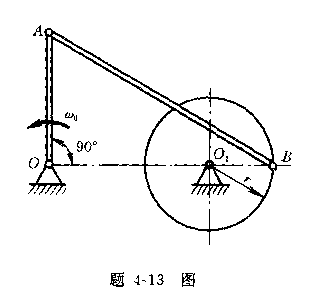
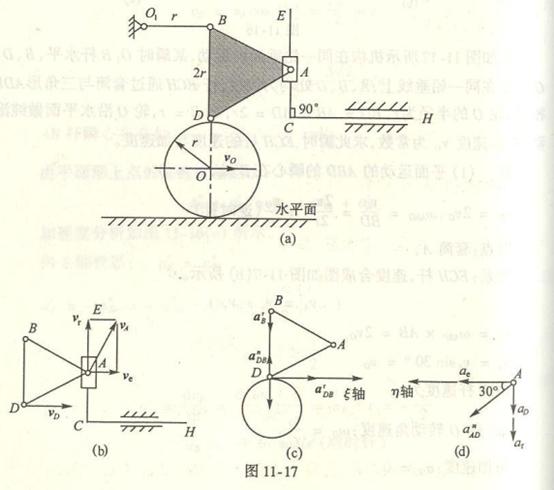
4-13长为0.2m的曲柄OA以匀角速度 ![]() =2rad/s转动,连杆AB长l=0.4m,半径r=0.1m的圆盘绕
=2rad/s转动,连杆AB长l=0.4m,半径r=0.1m的圆盘绕![]() 轴转动,在题4-13图所示位置
轴转动,在题4-13图所示位置
时,求B点的速度和加速度。
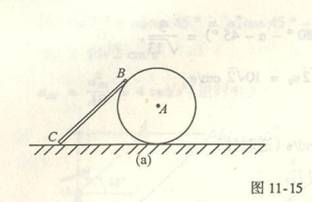
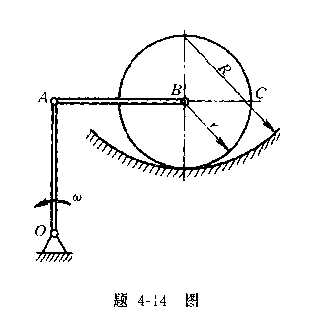
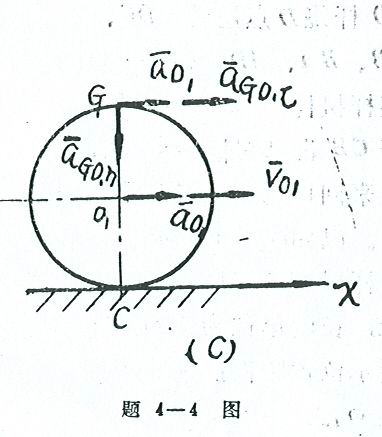
4-14曲柄OA以匀角速度![]() =2rad/s绕O轴转动,借助杆AB使半径为r的轮子运动,轮子沿半径R的圆槽作无滑动的滚动。已知:
=2rad/s绕O轴转动,借助杆AB使半径为r的轮子运动,轮子沿半径R的圆槽作无滑动的滚动。已知:
OA=AB=R=2r=1m,求图示位置时B点和C点的速度和加速度。
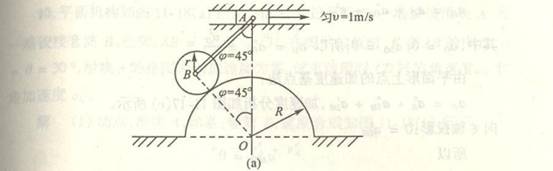
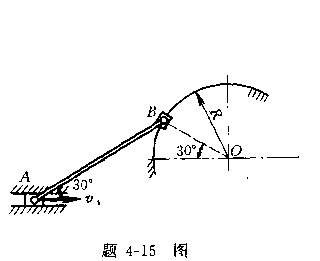
4-15杆AB的两端铰接有滑块A与B,其中滑块A沿水平方向向右以匀速度![]() =0.4m/s滑动,滑块B沿半径R=0.2m的圆弧滑动。已知
=0.4m/s滑动,滑块B沿半径R=0.2m的圆弧滑动。已知
AB=0.4m,试求在图示位置时,B点的速度和加速度及杆AB的角速度和角加速度。
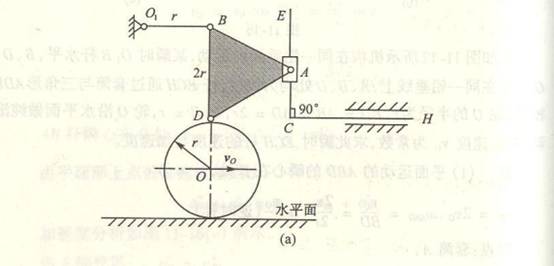
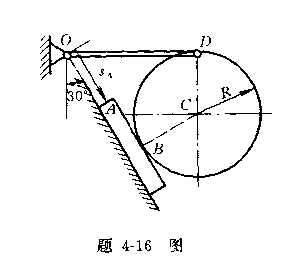
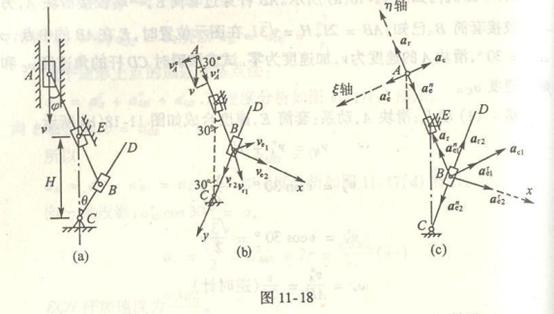
4-16平板A沿斜面按规律![]() =0.1
=0.1![]() +0.4t m运动,半径R=0.2m的圆盘沿平板无滑动的滚动。长0.4m的OD杆与滚子在D点铰接,并
+0.4t m运动,半径R=0.2m的圆盘沿平板无滑动的滚动。长0.4m的OD杆与滚子在D点铰接,并
绕O轴转动。当t=1s时,机构在图示位置,试求此时圆盘的角速度和角加速度以及B、C、D点的速度与加速度。
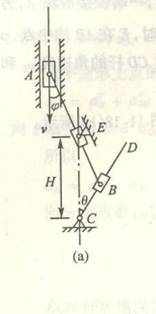
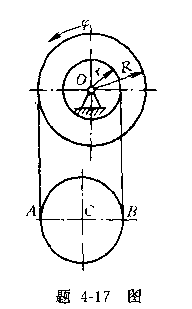
4-17鼓轮O的半径分别为r=0.1m,R=0.2m,按规律![]() =
=![]() -3t rad绕O轴转动。不可伸长的绳子绕在鼓轮O及滑轮C上。假定绳子与
-3t rad绕O轴转动。不可伸长的绳子绕在鼓轮O及滑轮C上。假定绳子与
鼓轮和滑轮无相对滑动,试求在t=1s时滑轮C的角速度和角加速度及滑轮C上A、B、C三点的速度和加速度。
4-18平行四边形铰接机构中两个曲柄OA与![]() D 用杆AD相连,滑块C沿着AD滑动,它通过杆BC与曲柄OA铰接。已知
D 用杆AD相连,滑块C沿着AD滑动,它通过杆BC与曲柄OA铰接。已知
OB=BA=0.1m。在图示位置时,曲柄角速度![]() =2 rad/s,角加速度
=2 rad/s,角加速度![]() =1 rad/s,试求滑块C的速度和加速度。
=1 rad/s,试求滑块C的速度和加速度。

参考答案
概念题答案:
9.1
9.3 9.2

![]()



9.4

9.4

9.5

9.6

9.7

9.8
9.9
![]()
9.10

9.11

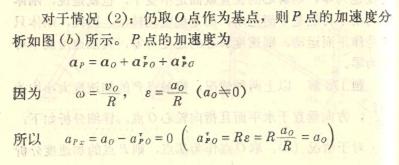
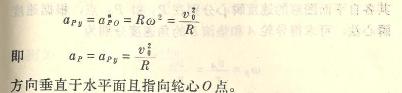
9.12

9.13

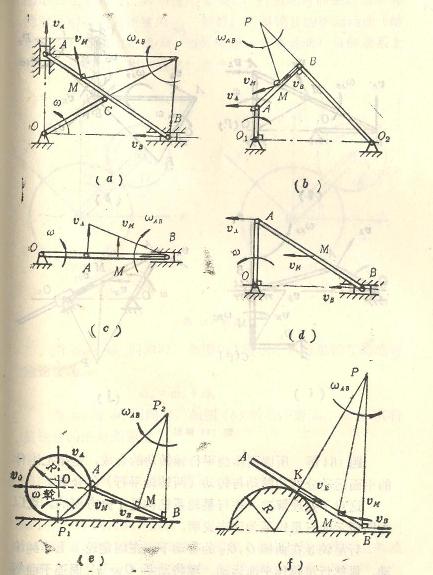
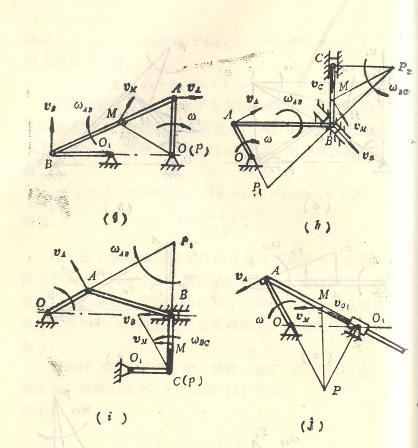
计算题答案:
9.1


9.2
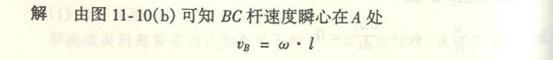
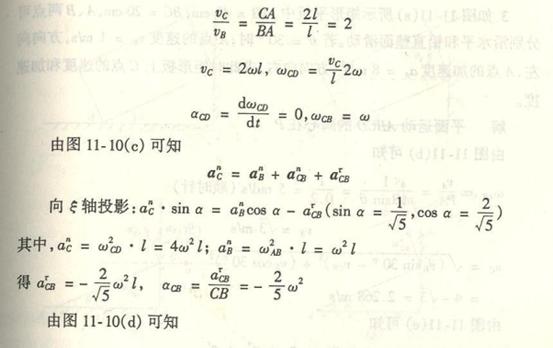
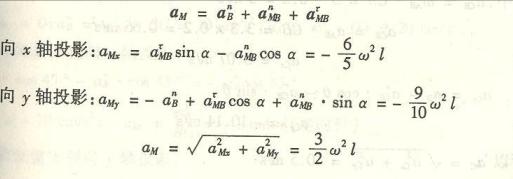
9.3


9.4

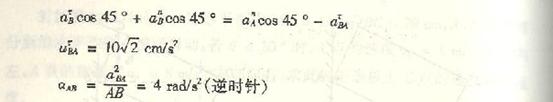
9.5
![]()
9.6
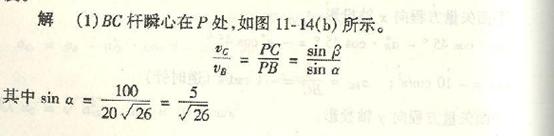

9.7
![]()
9.8

9.9


9.10



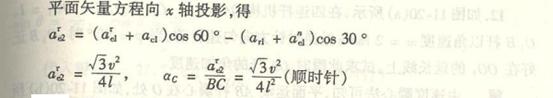
9.11

9.12

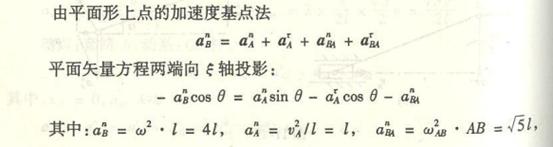
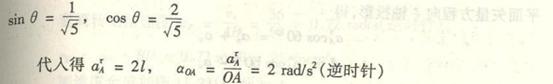
9.13

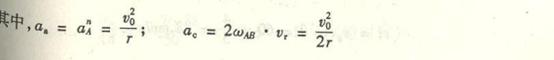
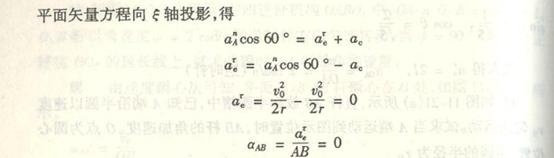
9.14
![]()
9.15

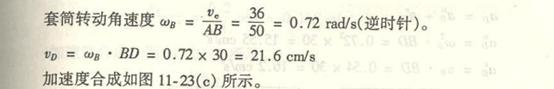
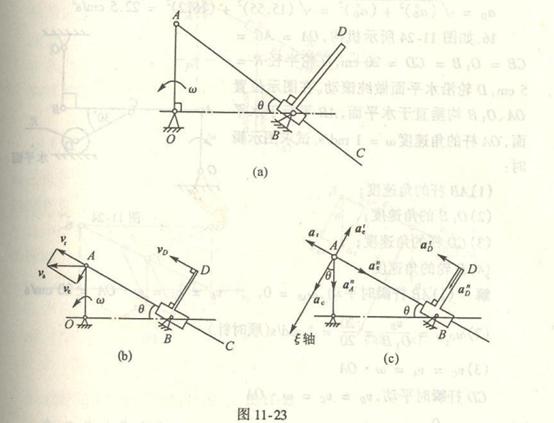

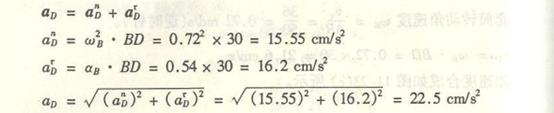
9.16

9.17

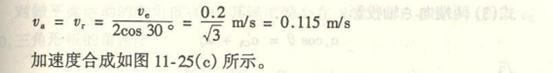


9.18




9.19

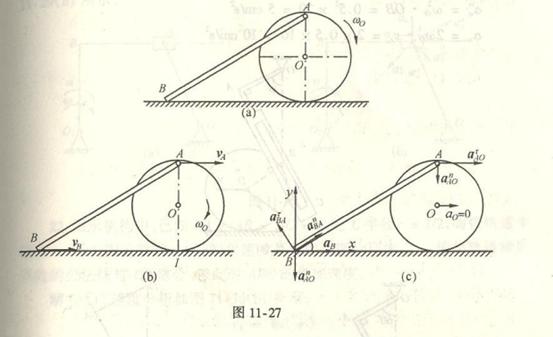
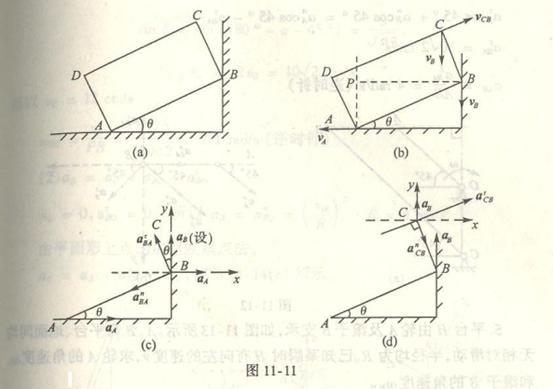
4-1解:
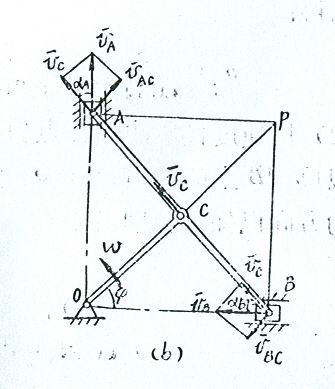
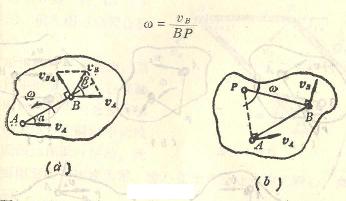
取AB杆为研究对象,AB杆作平面运动其上C点的速度v的大小和方向均可求得,其大小为:
![]()
方向垂直于曲柄OC。
(1)
用合成法求A点与B点的速度。
由于规尺AB上的C点的速度已知,所以选C点为基点。这样B点的运动,可以视为随基点C的平动与绕基点C的转动的合成运
动。
由速度合成法公式:
![]()
求未知量。在本题中,基点C的速度![]() 的大小和方向已经求得;B点相对于基点C的转动速度
的大小和方向已经求得;B点相对于基点C的转动速度![]() 方向垂直AB,大小未知;B点
方向垂直AB,大小未知;B点
的绝对速度v沿水平方向。这样,即可作出速度平行四边形,如图所示。由几何关系得
![]()
仍以C点为基点求A点的速度。A点的运动,可以视为随基点C的平动与绕基点C的转动的合成运动。
由速度合成法公式:
![]()
求A点的速度,在上式中,基点C的速度![]() 的大小和方向已求得;A点相对于基点C的转动速度
的大小和方向已求得;A点相对于基点C的转动速度![]() 的方向垂直AB,A点的绝对
的方向垂直AB,A点的绝对
速度![]() 方向沿铅直方向。这样可作出速度平行四边形,如图所示,由几何关系得:
方向沿铅直方向。这样可作出速度平行四边形,如图所示,由几何关系得:
![]()
(2)
用速度投影法求A点和B点的速度。因为规尺AB上的C点速度![]() 大小和方向均已求得,而A点和B点速度方向已知,分别
大小和方向均已求得,而A点和B点速度方向已知,分别
沿铅直与水平滑槽方向。根据速度投影定理,则有:
![]()
即
![]()
或
![]()
计算可得
![]()
(3)
用速度瞬心法求A点和B点的速度。
规尺AB作平面运动,A点和B点的速度![]() 和
和![]() 的方向已知,分别沿铅直与水平滑槽方向。过A、B点分别作
的方向已知,分别沿铅直与水平滑槽方向。过A、B点分别作![]() 、
、![]() 的垂线,其
的垂线,其
交点P就是规尺AB在图示位置瞬时的瞬心(见图b)。
因为C点是曲柄AC和规尺的联结点,C点的速度![]() 应同时满足这两构件的运动情况,即:
应同时满足这两构件的运动情况,即:
![]()
式中![]() 为AB杆在图示瞬时的角速度,
为AB杆在图示瞬时的角速度,
因此
![]()
A点的速度是
![]()
B点的速度是
![]()
4-2解:
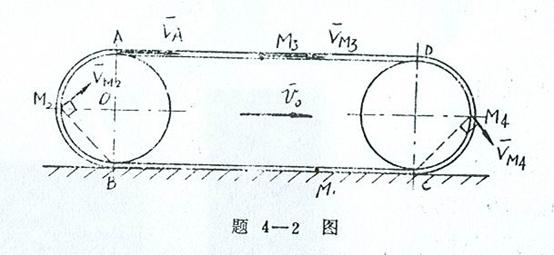
(1)分析运动。前后链轮作平面运动,沿地面滚动而不滑动;链条的运动分为三种:BC段在地面上静止不动,AD段作平动,A
![]() B段、C
B段、C![]() D段随链轮一起作平面运动。
D段随链轮一起作平面运动。
(2)求各点速度
![]() 点不动,故
点不动,故![]() ;
;
B点为后链轮的瞬心,链轮轮心O点的速度等于拖拉机的速度![]() ,设链轮的角速度为
,设链轮的角速度为![]() ,则有
,则有
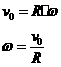
所以![]() 点的速度是
点的速度是
![]()
其方向垂直于B![]() ,如图所示。
,如图所示。
![]() 点是前链轮上的一个点,因为前后链轮半径相同,均为R,
点是前链轮上的一个点,因为前后链轮半径相同,均为R,
故前链轮的角速度也为![]() ,则
,则![]() 点的速度是
点的速度是
![]()
其方向垂直于![]() ,如图所示。
,如图所示。
因为AC段链条作平动,故![]() ,而
,而
![]()
4-3答:![]()
![]()
4-4解:
分析运动,选研究对象。机构中的曲柄OA作匀速定轴转动,连杆AB作平面运动,齿轮![]() 与
与![]() 作平面运动,杆
作平面运动,杆![]()
![]() 作平动,
作平动,
平台DE作平动。为了求平台的速度与加速度,需要选取连杆AB为研究对象,其次选取齿轮![]() 为研究对象。
为研究对象。
求连杆上B点速度。因为连杆上B点的速度方向与A的速度方向相同,如图a所示,故知连杆AB作瞬时平动,得
![]()
连杆![]()
![]() 作平动,图示瞬时其上各点速度相同,故有:
作平动,图示瞬时其上各点速度相同,故有:
![]()
选取齿轮![]() 为研究对象。它作平面运动,C点瞬时速度中心,设其角速度
为研究对象。它作平面运动,C点瞬时速度中心,设其角速度![]() ,则有
,则有
![]()
![]()
![]()
齿轮![]() 与平台DE相啮合的G点的速度为:
与平台DE相啮合的G点的速度为:
![]()
即为平台DE的速度,其方向垂直CG,水平向右。
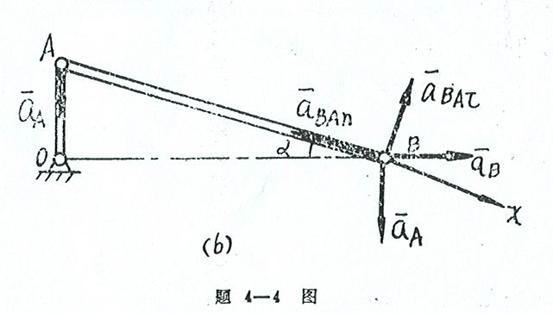
求平台DE的加速度。取连杆AB为研究对象。因为A点的加速度是已知的,故以A点为基点,则B点的运动,可以视为随基点A的
平动,与绕基点A的转动的合成运动。
根据加速度合成公式,列B点加速度表达式:
![]()
式中各加速度向量要素的已知和未知情况列表如下:
|
|
B点加速度 |
基点A的加速度 |
B点相对基点A的切向加速度 |
B点相对基点A的法向加速度 |
|
大小 |
未
知 |
曲柄作等速转动A点只有法向加速度
|
未
知 |
已
知 |
|
方向 |
方向沿直线轨迹 |
方向沿曲柄OA,指向O点 |
方向垂直AB,设指向如图B所示 |
沿BA方向 |
式中十个要素已经知道八个,故可求解。把各加速度向量画在图上,如图(b)所示。利用合向量投影定理,将各向量投影于x
轴上,得
![]()
![]()
![]()
![]()
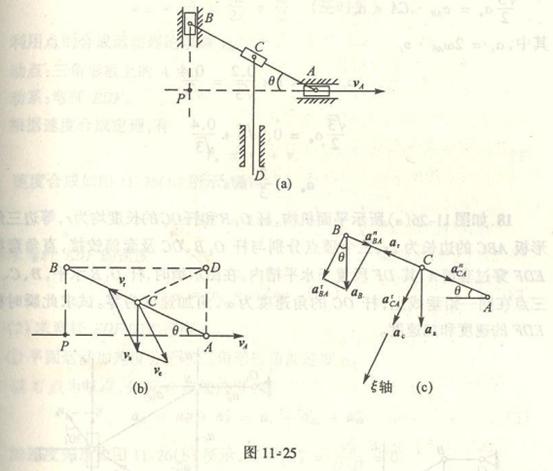
最后选齿轮![]() 为研究对象。
为研究对象。
因为连杆![]()
![]() 作平动,所以齿轮轮心
作平动,所以齿轮轮心![]() 的加速度,即
的加速度,即
![]()
其方向水平向右。选![]() 点为基点。根据加速度合成公式,列G点的加速度表达式:
点为基点。根据加速度合成公式,列G点的加速度表达式:
![]()
式中各加速度向量要素的已知和未知情况列表如下:
|
|
G点加速度 |
基点 |
G点相对于基点 |
G点相对于基点 |
|
大小 |
未知 |
已知:
|
已知 |
|
|
方向 |
未知 |
已知,如图(c)所示。 |
已知,方向垂直CG,设指向如图(c)所示。 |
已知,沿GC方向。 |
由表中可知,式中八个要素已知六个,故可求解,把各加速度向量画在图(c)上,利用合向量投影定理,将各向量投影于x轴
上
![]()
![]() 为齿轮G点加速度在水平方向的分量,也就是平台的加速度。
为齿轮G点加速度在水平方向的分量,也就是平台的加速度。
4-5答:![]()
4-6解:
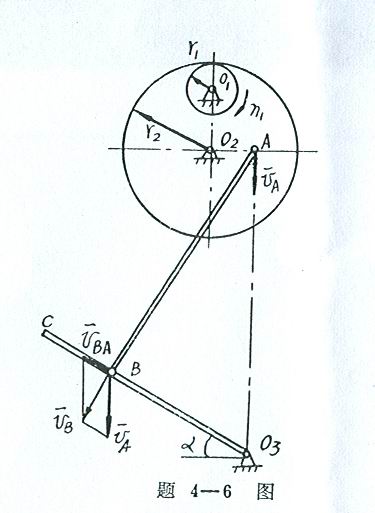
在该机构中,![]() 轮与
轮与![]() 轮作定轴转动,踏板
轮作定轴转动,踏板![]() C作转动,因此选AB连杆为研究对象。由于连杆AB上A点的速度可以预先求
C作转动,因此选AB连杆为研究对象。由于连杆AB上A点的速度可以预先求
出,故可以选A为基点,这样B点的运动,可以视为随基点A的平动和绕基点A的转动的合成运动。
根据速度合成法,列B点的速度表达式如下:
![]()
式中:![]() 为基点A的速度,其大小求法如下:
为基点A的速度,其大小求法如下:
![]() 轮的角速度是
轮的角速度是
![]()
![]() 轮的角速度是
轮的角速度是
![]()
A点的速度大小是
![]()
其方向垂直![]() A,指向如图所示;
A,指向如图所示;
![]() 为B点相对基点A的转动速度,其方向垂直杆AB,B点的绝对速度
为B点相对基点A的转动速度,其方向垂直杆AB,B点的绝对速度![]() 垂直踏板
垂直踏板![]() C。
C。
作B点速度平行四边形,如图所示。由图的几何关系,得B点的速度大小为
![]()
设C点的速度大小为![]() ,则
,则
![]()
![]()
![]()
4-7答:![]()
![]()
![]()
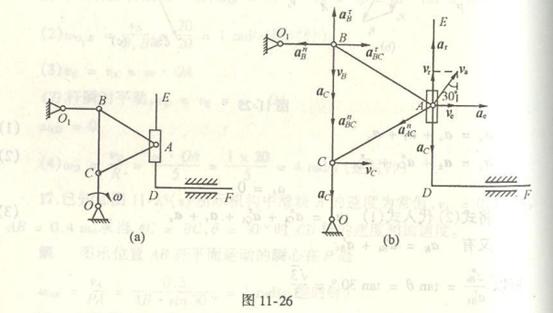
4-8解:
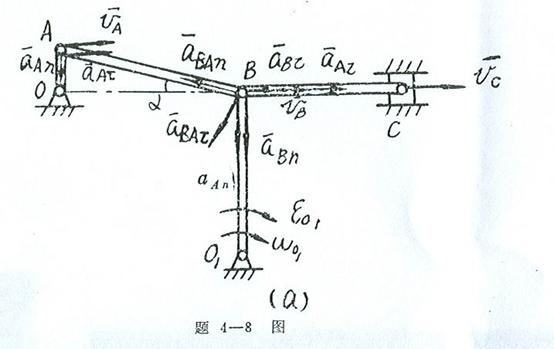
在该机构中,曲柄OA与杆OB作定轴转动,连杆AB与BC作平面运动,因此我们先选取连杆AB为研究对象。
因为连杆AB上的A点的速度![]() 的大小和方向都是已知的,即
的大小和方向都是已知的,即
![]()
其方向垂直于曲柄OA,水平向右。B点速度![]() 的方向与A点速度
的方向与A点速度![]() 的方向相同,故连杆AB在此瞬时作瞬时平动,所以有
的方向相同,故连杆AB在此瞬时作瞬时平动,所以有
![]()
同理,连杆BC在此瞬时也作瞬时平动,故
![]()
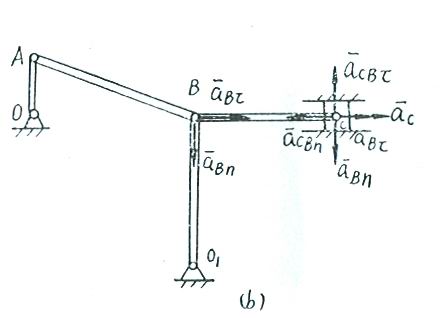
设![]() B杆的角速度为
B杆的角速度为![]() ,则有
,则有
![]()
![]()
![]()
其次求B点的加速度。
连杆AB上A点的加速度![]() 的大小和方向都是已知的。A点法向加速度
的大小和方向都是已知的。A点法向加速度![]() 的大小为
的大小为
![]()
其方向沿曲柄OA方向;A点切向加速度![]() 的大小为
的大小为
![]()
其方向垂直于曲柄OA。
选A为基点,根据加速度合成法,列B点的加速度表达式如下:
![]()
式中:
![]() ——B点绝对法向加速度,其大小
——B点绝对法向加速度,其大小
![]()
其方向沿杆![]() ;
;
![]() ——B点绝对切向加速度,其大小未知道,方向垂直于杆
——B点绝对切向加速度,其大小未知道,方向垂直于杆![]() ;
;
![]() ——B点绕基点A转动的法向加速度,因为连杆AB作瞬时平动,其角速度
——B点绕基点A转动的法向加速度,因为连杆AB作瞬时平动,其角速度![]() ,故
,故![]() ;
;
![]() ——B点绕基点A转动的切向加速度,其大小未知,方向垂直于杆AB。
——B点绕基点A转动的切向加速度,其大小未知,方向垂直于杆AB。
将各加速度向量画在B点上,如图(a)所示。用分析法求解,利用合向量投影定理,将B点加速度表达式中各向量投影于AB轴
上,得
![]()
![]()
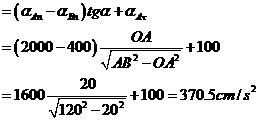
即:
![]() ,
,
![]()
最后求C点加速度![]()
BC杆作瞬时平动,虽然杆上各点速度相同,但各点加速度不相同。
在连杆BC上的加速度表达式如下:
![]()
式中:
![]() ——C点的绝对加速度,其大小是待求的未知量,方向沿滑槽水平方向;
——C点的绝对加速度,其大小是待求的未知量,方向沿滑槽水平方向;
![]() 与
与![]() ——分别为基点B的法向加速度与切向加速度,其大小与方向如前所述;
——分别为基点B的法向加速度与切向加速度,其大小与方向如前所述;
![]() ——C点绕B点转动的法向加速度,因为杆作瞬时平动,其角速度
——C点绕B点转动的法向加速度,因为杆作瞬时平动,其角速度![]() ,所以
,所以![]() ;
;
![]() ——是C点绕B点转动的切向加速度,方向垂直于杆BC,指向如图(b)所示,其大小未知。
——是C点绕B点转动的切向加速度,方向垂直于杆BC,指向如图(b)所示,其大小未知。
将C点加速度表达式中的各加速度向量画在C点上,如图(b)所示。用分析法求解,将C点各加速度向量投影于BC轴上,由合向
量投影定理得。
![]() 。
。
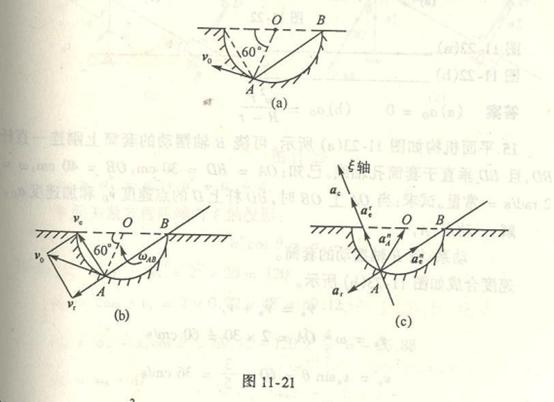
4-9解:
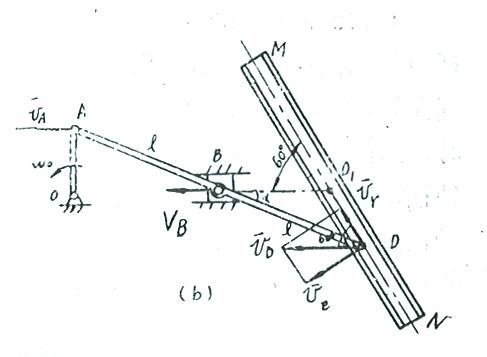
在研究的机构中,曲柄OA作定轴转动,连杆ABD作平面运动,滑道MN作定轴转动,滑块B作平动。选取连杆ABD为研究对象。
因为滑块B的速度![]() ,即连杆ABD上的B点的速度,其方向与A点速度
,即连杆ABD上的B点的速度,其方向与A点速度![]() 的方向相同,故知连杆ABD在图示瞬时作瞬时平动,则
的方向相同,故知连杆ABD在图示瞬时作瞬时平动,则
得![]() 。其方向水平向左。
。其方向水平向左。
因D点的绝对速度![]() 已知,滑块D在摆杆MN的滑槽中滑动,它与摆杆MN有相对运动,故取滑块D为动点,摆杆MN为动参考
已知,滑块D在摆杆MN的滑槽中滑动,它与摆杆MN有相对运动,故取滑块D为动点,摆杆MN为动参考
系。相对速度![]() 方向沿摆杆MN滑槽,其大小是待求的未知量;牵连速度
方向沿摆杆MN滑槽,其大小是待求的未知量;牵连速度![]() 为动参考系上D点相对定参考系的速度,其方向垂直
为动参考系上D点相对定参考系的速度,其方向垂直
MN,大小是未知的。
由速度合成定理,作D点速度平行四边形,如图所示。由图的几何关系得:
![]()
![]()
![]()
![]()
在三角形![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
![]()
![]()
设摆杆角速度为![]() ,则
,则
![]()
![]()
![]()
4-10答:![]()
4-11解:在此机构中,两曲柄OA与![]() 作转动,两连杆AD与DE作平面运动,杆EF作直线平动。分别选取连杆AD和DE为研究对
作转动,两连杆AD与DE作平面运动,杆EF作直线平动。分别选取连杆AD和DE为研究对
象。
应用瞬心法求未知量。因为杆EF作直线平动,故E点速度![]() 的方向沿铅垂向下,曲柄
的方向沿铅垂向下,曲柄![]() 作转动,故B点速度
作转动,故B点速度![]() 的方向垂直
的方向垂直
![]() 。所以连杆DE的瞬心可以求出。过E点与B点分别作速度向量
。所以连杆DE的瞬心可以求出。过E点与B点分别作速度向量![]() 与
与![]() 的垂线EP与BP,其交点P为连杆DE的瞬心,如图所
的垂线EP与BP,其交点P为连杆DE的瞬心,如图所
示。
其次,找连杆AD的瞬心。因为连杆AD上的D点速度![]() 方向已知,A点的速度
方向已知,A点的速度![]() 的方向垂直曲柄OA,所以,过A点与D点分别作
的方向垂直曲柄OA,所以,过A点与D点分别作
速度向量![]() 与
与![]() 的垂线AC与DC,其交点C则为连杆AD的瞬心。如图所示。
的垂线AC与DC,其交点C则为连杆AD的瞬心。如图所示。
由图的几何关系,则得A、D、E各点速度之间的关系式如下:
![]() (a)
(a)
![]() (b)
(b)
由(a)![]() (b)得
(b)得
![]() (c)
(c)
在(c)式中:![]()
![]()
![]() ,将所得各值代入(c)式,则得
,将所得各值代入(c)式,则得
![]()
因为杆EF作平动,所以锤头F的速度![]() 的大小是
的大小是
![]()
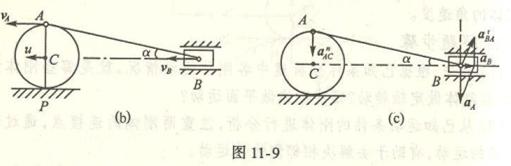
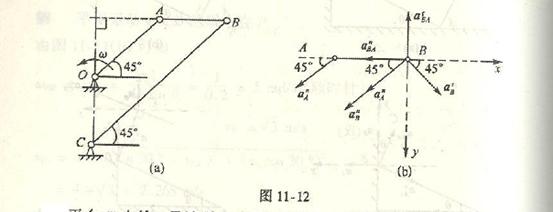
4-12解:在四连杆机构中,曲柄OA作定轴转动,![]() 杆也作定轴转动,杆AB作平面运动。我们选取杆AB为研究对象。
杆也作定轴转动,杆AB作平面运动。我们选取杆AB为研究对象。
由于连杆上A点的速度及加速度已知,所以选A点为基点,则B点的运动视为随基点A的平动与绕基点A的转动的合成运动。
根据速度合成法,列B点速度表达式
![]()
求未知量。
在题中,已知![]() 的大小:
的大小:![]() ,方向垂直OA。B点相对A点的转动速度
,方向垂直OA。B点相对A点的转动速度![]() 垂直AB,指向和大小未知。B点的绝对速度
垂直AB,指向和大小未知。B点的绝对速度![]()
垂直![]() 。作B点的速度平行四边形,由图可知,
。作B点的速度平行四边形,由图可知,![]() ,即B点为杆AB在图示瞬时的瞬心;并且,
,即B点为杆AB在图示瞬时的瞬心;并且,![]() ,
,
设AB杆的角速度为![]() ,则
,则
![]()
![]()
![]()
因为![]() ,所以
,所以![]() 杆的角速度
杆的角速度![]() 。
。
根据加速度合成法,列B点加速度表达式,
![]()
因为A、B点的绝对运动为圆周运动,B点相对于A点的运动也是圆周运动,故B点表达式可写成
![]()
式中:![]() ,
,![]() 为待求的
为待求的![]() 杆的角加速度,其方向垂直
杆的角加速度,其方向垂直![]() ;
;
![]() ,因为
,因为![]() 杆角速度
杆角速度![]() ,
,
![]() ,因为曲柄OA作匀速转动;
,因为曲柄OA作匀速转动;
![]() ,方向沿AO;
,方向沿AO;
![]() ,
,![]() 为AB杆角加速度,
为AB杆角加速度,![]() 的大小是未知的,而其方向垂直AB;
的大小是未知的,而其方向垂直AB;
![]() ,方向沿BA。
,方向沿BA。
将(a)式中各加速度向量画在图(b)中的B点上。由合向量投影定理,将(a)式中各加速度向量投影于预先选定的x、y轴
上,得
![]() (b)
(b)
![]() (c)
(c)
由(b)式:
![]()
![]()
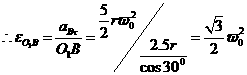
由(c)式:
![]()
![]()
![]()
![]() 为负值,说明AB杆的角加速度实际方向与图示方向相反。
为负值,说明AB杆的角加速度实际方向与图示方向相反。
求M点加速度。以A为基点,根据加速度合成法,列M点的加速度表达式:
![]()
(d)式中:
![]() ,方向沿AO;
,方向沿AO;
![]() ,其实际方向垂直AB,如图(b)所示;
,其实际方向垂直AB,如图(b)所示;
![]() ,方向沿MA;将(d)式各加速度向量画在图(b)的M点上,可得M点的加速度
,方向沿MA;将(d)式各加速度向量画在图(b)的M点上,可得M点的加速度![]() 的大
的大
小为
![]()
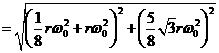
![]()