第四章 二元关系

1.填空：

1．如果A、B都是有限集，且|A|=m, |B|=n，则 |A´B |=( a )

2．A´Φ=Φ´B=( b )

2.设A={0,1}， B={a,b}，分别求A´B ，B´A，A´A 。

3.证明 (A∪B)´C= (A´C)∪(B´C)

4.名词解释

1．二元关系：

2．关系的定义域：

3．关系的值域：

5.X={a,b,c} Y={s} ，求X到Y的所有关系。

6.设|A|=n ，有多少个A上的关系？为什么？

7.选择填空： 如果|A|=m, |B|=n，则可以定义( )个从A到B的不同的关系。

供选择答案：A： mn B： mⁿ C： n^m D：2^mn

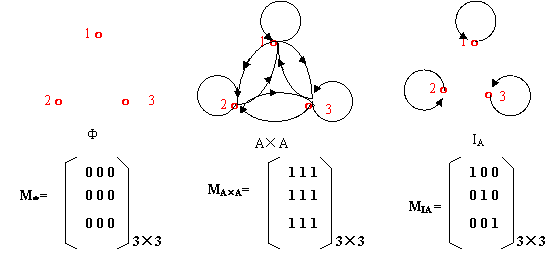
8.令A={2,3,5}，分别画出A上空关系Φ、完全关系(全域关系)、恒等关系I_A的关系图。再分别写出它们的矩阵。

9.设R是集合A中的关系，分别写出R是自反、反自反、对称、反对称、传递的谓词定义。

10.如何从R的关系图判断R是否有自反、反自反、对称、反对称性。

11.如何从R的关系矩阵判断R是否有自反、反自反、对称、反对称性。

12.判断下面命题的真值，并说明理由。

1．一个关系不是自反的，就是反自反的。

2．一个关系如果它是对称的，就不是反对称的。反之如果它是反对称的，就不是对称的。

13.设A={1,2,3}，给定A中如下四个关系，如图所示。

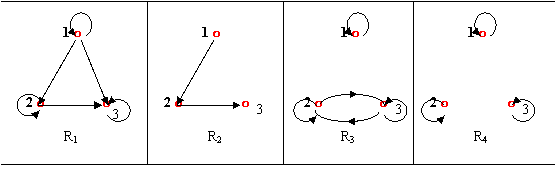
1．判断这四个关系是否有如下性质，用Y表示有，用N表示无，填下表。

	自反性	反自反性	对称性	反对称性	传递性
R1
R2
R3
R4

2．这四个关系中哪些是等价关系？是等价关系求对应的商集。哪些是偏序关系，对偏序关系画出哈斯图。

14.令I是整数集合，I上关系R定义为：

R={<x,y>|x-y可被3整除}，求证R是自反、对称和传递的。

15.设R是集合A上的一个自反关系, 求证：R是对称和传递的，

当且仅当 <a,b>和<a,c>在R中，则有<b,c>也在R中。

16. R和S都A上是自反、对称、传递的，求证R∩S也是自反、对称和传递的。

17.已知R是A上的反自反的、传递的二元关系，Ｒ是否是反对称的？为什么？

18.给定A={1,2,3},A中关系R和S如下：

R={<1,1>,<1,2>,<1,3>,<3,3>}

S={<1,1>,<1,2>,<2,1>,<2,2>,<3,3>}

分别求复合关系RoS， SoR，I_AoR, RoI_A 。

19. 已知F表示父子关系，M表示母子关系，S表示儿子与母亲关系，D表示女儿与母亲关系。问 FoF、FoS、 Do(DoM)分别表示什么关系？

20.填空，令R和S都是人类上的关系，且

R={<x,y>|x是y的父亲} S={<x,y>|x是y的母亲} 则

RoS表示( )关系。SoR表示( )关系。

RoS^C表示( )关系.

21.令R和S都是人类上的关系，且

R={<x,y>|x是y的父亲} S={<x,y>|x是y的母亲}，则

<x,y>ÎRoS 表示x是y的( )。

<x,y>ÎSoR 表示x是y的( )。

<x,y>ÎRoS^C表示x是y的( )。

22. 令RÍA×B SÍB×C TÍB×C 证明 Ro(S∪T)=(RoS)∪(RoT)

23.令RÍA×B SÍB×C TÍB×C 证明 Ro(S∩T)Í(RoS)∩(RoT)

24.R和S都是A上关系，判断下面命题的真值。并给予证明或者举反例说明之。

1．R和S都自反，RoS 也自反。

2．R和S都反自反，RoS 也反自反。

3．R和S都对称，RoS 也对称。

4．R和S都传递，RoS 也传递。

25.S是Ｘ上关系，证明Ｓ传递，当且仅当SoSÍＳ。

26. S是Ｘ上关系。证明Ｓ自反，当且仅当 I_XÍS。 (可用此定理判定自反)

27.S是Ｘ上关系，证明Ｓ是自反和传递，则SoS =S。其逆为真吗？

28.集合X上关系R和S都具有对称性。证明RoS是对称的充分和必要条件是

RoS = SoR。

29.R是A上关系，判断下面命题的真值。证明或者举反例说明之。

1．R自反，R^c也自反。

2．R对称，R^c也对称。

3．R传递，R^c也传递。

30.令R、S都是从X到Y的关系，证明 (R－S) ^C = R ^C－S ^C 。

31. 令R是从X到Y的关系，证明 (~R) ^C = ~R ^C 。

32.令R是从X到Y的关系，S是Y到 Z的关系，则

(RoS) ^C = S ^CoR ^C 。

33.R是A上关系，证明R是对称的，当且仅当 R ^C =R 。

34.R是A上关系，证明R是反对称的，当且仅当 R∩R ^C ÍI_A。

35.R的有向图如图所示，求r(R)、s(R)、t(R)。

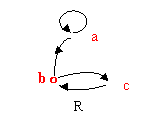
36.R1和R2是A上关系，且R2 ÍR1，求证

a) r(R2) Ír(R1), b) s(R2) Ís(R1), c) t(R2) Ít(R1)。

37.R1和R2是A上关系，求证

a) r(R1∪R2)= r(R1)∪r(R2) ,

b) s(R1∪R2)= s(R1)∪s(R2) ,

c) t(R1)∪t(R2) Í t(R1∪R2)。

38.令X={1,2,3}, 下面哪些集合是A的覆盖？哪些是A的划分？哪些是A的最大划分？哪些是A的最小划分？

A1={{1,2,3}}, A2={{1},{2},{3}}, A3={{1,2},{3}},

A4={{1,2},{2,3}}, A5={{1},{3}}

39.令A={1,2,3,4}，A有多少个不同的划分？请分别写出这些划分。

40.给定集合A={1,2,3},定义A上的关系如下：

R={<1,1>,<1,2>,<1,3>,<3,3>}

S={<1,1>,<1,2>,<2,1>,<2,2>,<3,3>}

T={<1,1>,<2,1>,<2,2>,<2,3>,<3,3>}

M=Ф(空关系)

N=A×A(完全关系（全域关系）)

1. 分别画出上述各个关系的有向图。

2. 用“√”表示“是”，用“×”表示“否”，填下表：

	自反的	反自反	对称的	反对称	传递的
R
S
T
M
N

3. 上述五个关系中，哪些是等价关系？哪些是偏序关系？是等价关系，写出相应的商集。是偏序关系，画出相应的哈斯图，以及A的极小元、极大元、最小元、最大元、上界与下界。

4. 分别求复合关系 RoS 和闭包t(R)

41.令集合A={1,2,3,4},给定A上的关系R₁,R₂,R₃,R₄如下:

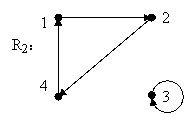
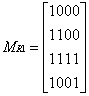
R₃={<1,1>,<2,2>,<2,3>,<2,4>,<3,2>,<3,3>,<3,4>,<4,2>,<4,3>,<4,4>}

R₄={<1,1>,<1,2>,<1,4>,<2,1>,<2,2>,<2,3>,<3,2>,<3,3>,<3,4>,<4,1>,<4,2>,<4,3>,<4,4>}

1. 分别画出复合关系~R₄oR₂^c 和闭包s(R₂)的有向图.

2. 用“∨”表示“是”,用“×”表示“否”填下表:

	自反的	反自反的	对称的	反对称的	传递的
R1
R2
R3
R4

3. R₁,R₂,R₃,R₄中哪些是等价关系? 哪些是偏序关系?

如果是等价关系,请写出该等价关系对A的商集.

如果是偏序关系,请画出它的哈斯图,并写出{2,4}的极小元、极大元、最小元、最大元、上界和下界。

42. R和S都是A上等价关系,下面哪个是A上等价关系?证明或举反例说明之.

a) R∪S b) R∩S c) ~R (即A×A-R)

d) R-S e) R² f) r(R-S)

43.R是A上是等价关系，设

S={<a,b>|$c∈A∧<a,c>∈R∧<c,b>∈R}

求证S也是等价关系。

44. R是A上对称和传递的关系，证明如果"a∈A，,$b∈A，使得<a,b>∈R，则R是一个等价关系。

45.令A是正整数集合,定义A×A中关系R如下:任何<a,b>,<c,d>ÎA×A

<a,b>R<c,d> 当且仅当 a+d=b+c

1. 证明R是A×A上等价关系。

2. 令A={1,2,3}，R是上述等价关系，求商集A×A/R。

46.令R是A上的有自反、传递性的二元关系，在A上又定义一个关系E，其定义如下：

xEy<=>xRy∧yRx 其中x,y∈A

1．证明E是A上的等价关系。

2．在A/E上又定义关系S,其定义如下：

[x]_ES[y]_E<=>xRy 其中[x]_E,[y]_E∈A/E

求证，S是A/E上的偏序关系。

47.令R是A上等价关系，[a]表示a相对等价关系R的等价类。证明下面命题彼此等价：

(1). aRb (2). [a]=[b] (3).[a]∩[b]≠Φ

48.令A={1,2,3,4}， R是A上等价关系。且商集|A/R|=3，则这样的R有多少个？请分别写出这样的等价关系所对应的商集。再任选其中一个商集画出所对应的等价关系的有向图。

49.设A={1,2,3,4}， R、S都是A上不同的等价关系。且已知RÇS的商集如下：

A/RÇS ={{1}，{2}，{3,4}}

画出相应的等价关系R和S的有向图 。（求一种答案即可）

50.已知R是A中等价关系，A={1,2,3,4} 且R＝{<1,1>,<1.2>,<2,4>}。

问tsr(R)是不是A中等价关系? 如果不是等价关系，说明理由。如果是等价关系，求商集A/tsr(R)。

51. 已知R是A中自反关系，求证,如果R=RοR^C ,证明R是A上等价关系。

52.判断下列各命题的真值，并说明理由。

1．R是A上的任何二元关系，则trs(R)都是A上的等价关系。

2．R是A上的对称和传递的二元关系，则由于下面命题公式

"x"y((xÎAÙyÎAÙ< x,y >ÎRÙ< y,x >ÎR) ®< x,x > ÎR)

真值为真，所以R是自反的。

3．R是A上的二元关系，仅当下面谓词公式

Ø$x$y(xÎAÙyÎAÙ< x,y >ÎRÙ< y,x >ÎR)

在论域A上为真，R才是反对称的。

MR=

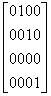
53.令A={1,2,3,4},给出A中关系R的矩阵M_R如下：

试问ts(R)是否为A上的等价关系？

如果是，请写出商集A/ts(R).

如果不是，请说明理由。

54.从给出的供选择的答案中选择出正确的答案。

已知R是X上的二元关系，任何a∈X，定义集合R(a)如下：

R(a)={x| x∈X,<a,x>∈R}

显然R(a)ÍX，令X＝{-1,-2,0,1,2,3,4}，令R₁,R₂,R₃是X上关系定义如下：

R₁={<x,y>| x,y∈X Ù x<y }

R₂ ={<x,y>| x,y∈X Ù y-1<x<y+2 }

R₃={<x,y>| x,y∈X Ù x²≤y }

则下列集合满足：

1． R₁ (0)=A

2． R₂ (0)=B

3． R₃ (3)=C

供选择的答案：

A，B，C，D：⑴ Φ；⑵ {-1,-2,0}； ⑶ {-2,-1}； ⑷ {-1, 0,1}； ⑸ {-1,0}；⑹{1,2,3}； ⑺{2,3,4}；⑻ {1,2,3,4}；⑼ 以上结果都不对。

55. 已知R是A上的二元关系，任何a∈A,定义集合R(a)如下：

R(a)={x| x∈A,<a,x>∈R}

1．分别说明如何用R(a)，来定义R有自反、反自反、对称、反对称以及传递性。

2．如果R是A上的等价关系，如何用R(a)表示商集A/R?

56. 令R是A中关系，任意a∈A，定义集合R(a)如下：

R(a)={x|<a,x>∈R}

试证明R是等价关系时，<a,b>∈R，当且仅当R(a)=R(b)。

57. 令Ａ＝{a,b,c,d,e,f,g}，R,S是集合Ａ上的等价关系，已经知道R∩S也是A上的等价关系。如果集合A对R、S 的商集分别是：

A/R={{a,b,c},{d,e,g,f}}

A/S={{a,c},{b,d},{e,f,g}

试求A/R∩S。

58. 已知R是A中二元关系，且对任何aÎA,存在bÎA,使得<a,b>ÎR,且R=RοR^C ,求证,R是A上等价关系。

59. 已知R是A中等价关系，

1．证明RοR也是A中等价关系。

2．令A＝{1,2,3}, R={<1,1>,<2,2>,<3.3>,<2,1>,<1,2>},求商集A/RοR.

60.设X={1,2,3} Y={1,2}, 在X的幂集P(X)上定义二元关系R如下：

对于任何A,B∈P(X), ARB 当且仅当 AÈY=BÈY

1.画出关系R的有向图.

2.R是等价关系吗?如果是,请写出商集P(X)/R. 如果不是请说明原因

61. R是A上等价关系，将表达式(R⁺∪I_A)^*∪tsr(R∩R^c)化简。(要有化简过程，且每一步在后面注明做此步的根据是什么。)

62. 给定集合A={a,b,c,d,e,f,g}，R₁、R₂是A上等价关系，且已知R₁和R₂确定的两个商集分别是:

A/R₁={{a,b,c},{d,e,f,g}}

A/R₂={{a,c},{b.d},{e,f,g}}

1.显然R₁ÇR₂也是A上等价关系，试求商集A/ R₁ÇR₂ 。

2.任取xÎA, 试指出等价类[x]_R1ÇR2与[x]_R1、[x]_R2之间的关系，并对你的回答给予证明。

63. 给定集合Ａ＝{a,b,c,d,e,f,g}，R₁、R₂是A上的等价关系，显然R₁∩R₂.也是A上的等价关系。又已知商集:

A/R₁={{a,b,c},{d,e,g,f}}

A/R₂={{a,c},{b,d},{e,f,g}}

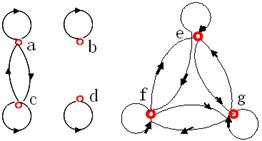
画出R₁∩R₂的有向图，再求商集A/R₁∩R₂ 。

64. 给定A上相容关系r的简化图如下，求完全覆盖Cr(A)。

65. X={x1,x2, x3, x4, x5, x6}, r是X上相容关系，其简化关系矩阵如下,求X的完全覆盖。

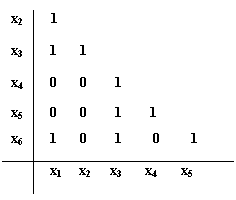
66.已知X={1,2,3,4,5,6,7}上的相容关系r的简化矩阵为:

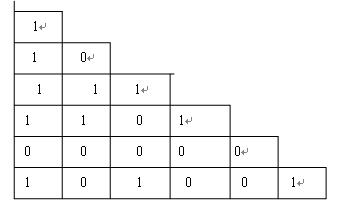
求完全覆盖Cr(X)

67.已知A是正整数集合，在A上定义关系Ｒ如下：

Ｒ＝{<x,y>ㄧx∈Ａ，y∈Ａ，x可以整除y}

求证Ｒ是A上的偏序关系。

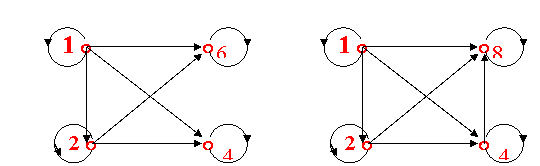
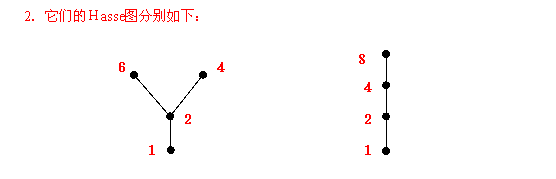
68.设集合A={1,2,4,6},B={1,2,4,8}, ≤是整除关系，

1．首先分别画出偏序集<A,≤>、<B,≤>的有向图。

2．再分别画出它们的哈斯图。

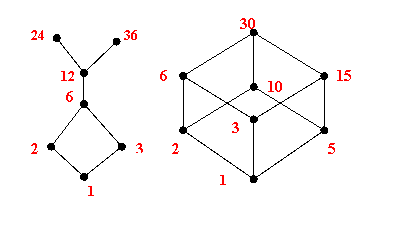
69. 设C={1,2,3,6,12,24,36}, D={1,2,3,5,6,10,15,30}，≤ 是C、D上整除关系。

1. 请画出<Ｃ,≤>, <Ｄ,≤>的Hasse图。

2．在<Ｃ,≤>中，分别求{2,3}和{6,12,24}的极小元、极大元、最小元、最大元、上界、下界、上确界和下确界。

70. 设S={0,1}，F是S中的符号构成的长度不超过3的符号串的集合，即

F={λ,0,1,00,01,10,11,000,001,010,011,100,101,110,111}

其中λ表示空符号串(即没有字符的符号串,λ的长度为0), 在F上定义关系R如下：

对于任何x,y∈F，

<x,y>∈R Û x是y的前缀.

例如0是00和01的前缀，但是01不是001的前缀。

1．求证R是F上的偏序关系.

2．画出R的哈斯图.

3．求F的极小元和最大元.

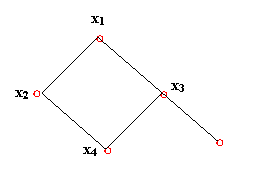
71. 令P={x1,x2, x3, x4, x5}, P上偏序关系的Hasse图如图所示，求子集 {x1,x2, x3}，

{x2, x3, x4}，{x3, x4, x5}和P的极小(大)元、最小(大)元、上界、下界、最小上界和最大下界(上确界和下确界)。

72. 给出偏序集<A,R>，其哈斯图如下图所示。 画出~R的有向图。

1

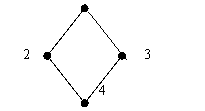
73. 给定集合A＝{a,b,c,d,e}，≤是A上的偏序关系。偏序集<A, ≤>的哈斯图如下：

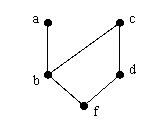
1．求集合A的极大元、极小元、最小元、最大元。

2．子集{b,f}的上界、下界。

3．画出偏序关系≤的关系图。

1.答案：a：( mn ) b； (Φ)

2.答案：解： A´B={<0,a>,<0,b>,<1,a>,<1,b>}

B´A={<a,0 >,<b,0>,<a,1>,<b,1>}

A´A={<0,0>,<0,1>,<1,0>,<1,1>}

3.答案：证明：任取<x,y>Î(A∪B)´C

Û x ÎA∪B Ù y ÎC Û (xÎA∨xÎB) Ù yÎC Û( xÎA ÙyÎc)∨(xÎbÙyÎC)

Û<x,y>ÎA´C∨<x,y>ÎB´C Û<x,y>Î(A´C)∪(B´C)

所以(A∪B)´C= (A´C)∪(B´C)

4.答案：

1．二元关系：:设A、Ｂ是集合，如果ＲÍA×B，则称R是一个从A到B的二元关系。如果 RÍA×A，则称R是A上的二元关系。

2．关系的定义域：设RÍA×B，由R中所有序偶<x,y>的第一个元素x 组成的集合，称为R的定义域，记作dom R。即

dom R={x|$y(<x,y>ÎR)}

3．关系的值域：设RÍA×B，由R中所有序偶<x,y>的第二个元素 y 组成的集合，称为R的值域，记作ran R。即

ran R={y|$x(<x,y>ÎR)}

5.答案： X×Y={<a,s>,<b,s>,<c,s>}

X×Y的任何一个子集都是一个 从X到Y的关系。如果|X|=m |Y|=n则有2^mn个从X到Y的关系, 故,有2³=8个关系:

R0=Φ R1={<a,s>} R2={<b,s>} R3={<c,s>}

R4={<a,s>,<b,s>} R5={<a,s>,<c,s>} R6={<b,s>,<c,s>}

R7={<a,s>,<b,s>,<c,s>}

6.答案：因为RÍA×A,所以A×A有多少个子集就有多少个A上关系,由集合的幂集就是该集合的子集构成的,所以A上关系个数就是A×A 的幂集P(A×A)的元素个数|P(A×A)|。即有2ⁿⁿ 个关系。

7.答案：(D)。

8.答案：A上的空关系Φ、完全关系A×A及I_A的关系图及矩阵如下：

9.答案：

R是A中自反的Û"x(xÎA®<x,x>ÎR)

R是A中反自反的Û"x(xÎA®<x,x>ÏR)

R是A上对称的Û"x"y((xÎAÙyÎAÙxRy) ®yRx)

R是A上反对称的Û"x"y((xÎAÙyÎAÙxRyÙyRx) ®x=y)

R是A上传递的关系Û"x"y"z((xÎAÙyÎAÙzÎAÙxRyÙyRz)®xRz)

10.答案：

从关系有向图看自反性：每个结点都有环。

从关系有向图看反自反性：每个结点都无环。

从关系有向图看对称性：在两个不同的结点之间，若有边的话，则有方向相反的两条边。

由R的关系图看反对称性：两个不同的结点之间最多有一条边。

11.答案：

从关系矩阵看自反性：主对角线都为1。

从关系矩阵看反自反性：主对角线都为0。

从关系矩阵看对称性：以主对角线为对称的矩阵。

从关系矩阵看反对称性：以主对角线为对称的两个元素中最多有一个1。

12.答案：

1．真值为假。

例如，下面关系既不是自反的，也不是反自反的。

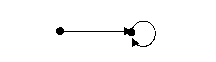
2．真值为假。如空关系和恒等关系。它们既是对称的，又是反对称性的。

13.

1．判断这四个关系是否有如下性质，用Y表示有，用N表示无，填下表。

	自反性	反自反性	对称性	反对称性	传递性
R1
R2
R3
R4

2．这四个关系中哪些是等价关系？是等价关系求对应的商集。哪些是偏序关系，对偏序关系画出哈斯图。

答案：1.

	自反性	反自反性	对称性	反对称性	传递性
R1	Y	N	N	Y	Y
R2	N	N	N	Y	N
R3	Y	N	Y	N	Y
R4	Y	N	Y	Y	Y

2．R₃和R₄是等价关系。A/R₃ ={{1},{2,3}}, A/R₄ ={{1},{2},{3}}

R₁是偏序关系。其哈斯图如下：

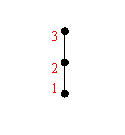
14.答案：证明：⑴ 证自反性：任取x∈I, (要证出<x,x>ÎR )

因 x-x=0, 0可被3整除,所以有<x,x>∈R, 故R自反。

⑵ 证对称性：任取x,y∈I,设<x,y>∈R, (要证出 <y,x>ÎR )

由R定义得 x-y可被3整除, 即x-y=3n(n∈I)，

y-x=-(x-y)=-3n=3(-n), 因-n∈I, ∴<y,x>∈R, 所以R对称。

⑶证传递性:任取x,y,z∈I,设xRy, yRz, (要证出xRz)

由R定义得 x-y=3m, y-z=3n (m.n∈I)，x-z= (x-y)+(y-z)=3m+3n=3(m+n),

因m+n∈I, 所以xRz, 所以R传递。 证毕

15答案：证明：必要性: 已知R是对称和传递的。 设<a,b>ÎR 又<a,c>ÎR，(要证出 <b,c>ÎR )。

因R对称的故<b,a>ÎR，又已知<a,c>ÎR， 由传递性得<b,c>ÎR。所以有如果<a,b>和<a,c>在R中, 则有<b,c>也在R中。

充分性: 已知任意 a,b,cÎA， 有 <a,b>ÎR Ù<a,c>ÎR Þ <b,c>ÎR

先证R对称：任取 a,bÎA 设<a,b>ÎR ，(要证出 <b,a>ÎR )

因R是自反的，所以<a,a>ÎR，由<a,b>ÎR且<a,a>ÎR，根据已知条件得<b,a>ÎR ，所以R是对称的。

再证R传递：任取 a,b,cÎA 设<a,b>ÎR, <b,c>ÎR。(要证出<a,c>ÎR )

由R是对称的,得<b,a>ÎR ,由<b,a>ÎR且<b,c>ÎR,根据已知条件得<a,c>ÎR ，所以R是传递的。

16.答案：证明：

1．证明R∩S的自反性。

任取 x∈A, (证出<x,x>∈R∩S)

因R和S都自反，所以有<x,x>∈R，<x,x>∈S，于是有<x,x>∈R∩S，所以R∩S也自反。

2．证明R∩S的对称性：

任取 x,y∈A,设<x,y>∈R∩S, (证出 <y,x>∈R∩S。)

则<x,y>∈R，<x,y>∈S，因为R和S对称，所以有<y,x>∈R，<y,x>∈S，于是<y,x>∈R∩S。∴R∩S对称。

3．证明R∩S的传递性：

任取 x,y,z∈A, 设<x,y>∈R∩S,<y,z>∈R∩S, (证出<x,z>∈R∩S)

<x,y>∈R∩S∧<y,z>∈R∩S

Û <x,y>∈R∧<x,y>∈S∧<y,z>∈R∧<y,z>∈S

Û (<x,y>∈R∧<y,z>∈R)∧(<x,y>∈S ∧<y,z>∈S)

Þ <x,z>∈R∧<x,z>∈S （因为R、S传递）

Û <x,z>∈R∩S 所以R∩S传递。

17.答案：解：R是A上的反自反的、传递的二元关系，则Ｒ一定是反对称的。因为

如果R是空关系时，结论显然是正确的。

如果R不是空关系时。假设R不是反对称的，必有<x,y>∈R，也有<y,x>∈R。再根据传递性得<x,x>∈R。这就与R反自反矛盾。所以R一定是反对称的。

18.答案：解 RoS={<1,1>,<1,2>,<1,3>,<3,3>}

SoR={<1,1>,<1,2>,<1,3>,<2,1>,<2,2>,<2,3>,<3,3>}

I_A＝{<1,1>,<2,2>,<3,3>}

I_AoR= RoI_A =R。

19.答案：解 FoF：a ® b ® c

父 ®子(父® 子)

FoF：表示祖孙关系。

FoS ： a ® b ® c

父® 子 ® 母

FoS：表示夫妻关系

Do(DoM): a ® b ® c ® d

女儿 ®母(女® 母 ® 子)

Do(DoM): 表示外甥女与舅舅关系

20.答案：RoS表示( 外祖父与外孙 )关系。SoR表示( 祖母与孙子 )关系。

RoS^C表示( 夫妻 )关系.

21.答案：<x,y>ÎRoS 表示x是y的( 外公 )。

<x,y>ÎSoR 表示x是y的( 祖母 )。

<x,y>ÎRoS^C表示x是y的( 丈夫 )。

22.答案：证明 任取<a,c>∈Ro(S∪T)

Û $b(b∈B∧<a,b>∈R∧<b,c>∈S∪T)

Û$b(b∈B∧<a,b>∈R∧(<b,c>∈S∨<b,c>∈T))

Û$b((b∈B∧<a,b>∈R∧<b,c>∈S)∨(b∈B∧<a,b>∈R∧<b,c>∈T))

Û$b(b∈B∧<a,b>∈R∧<b,c>∈S)∨$b(b∈B∧<a,b>∈R∧<b,c>∈T)

Û<a,c>∈RoS∨<a,c>∈RoT

Û<a,c>∈(RoS)∪(RoT)

所以Ro (S∪T)=(RoS)∪(RoT)

23.答案：证明 任取<a,c>∈Ro (S∩T)

Û $b(b∈B∧<a,b>∈R∧<b,c>∈S∩T)

Û$b(b∈B∧<a,b>∈R∧(<b,c>∈S∧<b,c>∈T))

Û$b((b∈B∧<a,b>∈R∧<b,c>∈S)∧(b∈B∧<a,b>∈R∧<b,c>∈T))

Þ$b(b∈B∧<a,b>∈R∧<b,c>∈S)∧$b(b∈B∧<a,b>∈R∧<b,c>∈T)

Û<a,c>∈RoS ∧<a,c>∈RoT

Û<a,c>∈(RoS)∩(RoT)

所以 Ro (S∩T)Í(RoS)∩(RoT)

24.答案：1．真值为真。即R和S都自反，RoS 一定自反。

因为任取a∈A, 由于R和S都自反， 所以<a,a>∈R 及<a,a>∈S 故<a,a>∈RoS ∴ RoS 自反。

2．真值为假。即R和S都反自反，RoS 不一定反自反。举反例见下图。

3．真值为假。即R和S都对称，RoS 不一定对称。举反例见下图。

4．真值为假。即R和S都传递，RoS 不一定传递。举反例见下图。

25.答案：证明：充分性，已知SoS ÍＳ

任取x,y,z∈X, 且有<x,y>∈S,<y,z>∈S, 根据关系的复合得<x,z>∈SoS ,由已知得<x,z>∈S ,所以Ｓ传递。

必要性，已知Ｓ传递，

任取<x,y>∈SoS ,根据关系的复合得，$z(z∈X∧<x,z>∈S∧<z,y>∈S),

由Ｓ传递得<x,y>∈S，所以SoSÍＳ

26.答案：证明：充分性，已知I_X ÍS，

任取x∈X, 有<x,x>∈IX , 由已知得<x,x>∈S, 所以Ｓ自反。

必要性，已知Ｓ自反，

任取<x,y>∈I_X , 得x=y, 而S自反，所以<x,y>∈S ∴I_X ÍS。

27.答案：首先证明SoSÍＳ：

任取<x,y>∈SoS，根据关系的复合得，$z(z∈X∧<x,z>∈S∧<z,y>∈S)，

由Ｓ传递得<x,y>∈S，所以SoSÍＳ

再证明SÍ SoS。　

任取<x,y>∈S, 又已知Ｓ自反，所以<x,x>∈S,于是有<x,x>∈S∧<x,y>∈S，由关系的复合得<x,y>∈SoS，所以有SÍSoS。

最后得SoS＝Ｓ。　

其逆不一定为真。例如S如图所示：满足SoS＝Ｓ，S虽然传递，但不自反。

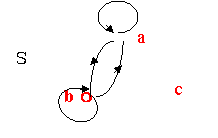
28.答案：充分性：已知RoS = SoR。

任取<x,y>∈RoS，根据关系的复合得，$z(z∈X∧<x,z>∈R∧<z,y>∈S)，

根据R和S都具有对称性，得 $z(z∈X∧< z , x>∈R∧<y,z>∈S)，根据关系的复合得，< y, x >∈S o R，又已知RoS = SoR。所以< y, x >∈R o S。因此R o S对称

必要性：已知RoS是对称的。

先证明RoS Í SoR。任取<x,y>∈RoS，因为RoS是对称的，所以< y, x >∈RoS，根据关系的复合得，$z(z∈X∧<y,z>∈R∧<z,x>∈S)，

根据R和S都具有对称性，得 $z(z∈X∧< z , y>∈R∧<x,z>∈S)，根据关系的复合得，< x, y>∈S o R，所以RoS Í SoR。

同理可证，SoR Í RoS。

最后得RoS = SoR。

29.答案：

1．真值为真，即R自反，R^c也自反。

因为任取x∈A,因R自反，所以<x,x>∈R，所以 <x,x>∈ R^c 。

2．真值为真，即R对称，R^c也对称。

因为R对称，所以R^c =R ∴ R^c也对称。

3．真值为真，即R传递，R^c也传递。

任取x,y,z∈A，且有<x,y>∈R^c ，<y,z>∈R^c，于是<y,x>∈R ,<z,y>∈R，因R传递，所以<z,x>∈R，于是有<x,z>∈R^c，∴ R^c传递。

30.答案：证明 任取<y,x>Î(R－S)^C，则

<y,x>Î(R－S) ^C Û <x,y>Î(R－S)

Û <x,y>ÎR∧<x, y>ÏS

Û <y,x>ÎR ^C∧<y,xÏS ^C

Û<y,x>Î R ^C－S ^C

所以 (R－S) ^C = R ^C－S ^C 。

31.答案：证明：任取<y,x>∈(~R) ^C Û<x,y>∈~RÛ<x,y>ÏR

Û<y,x>ÏR ^C Û<y,x>∈~R ^C ∴ (~R) ^C =~R ^C 。

32.答案：证明：任取<z,x>∈(RoS) ^C

Û<x,z>ÎRoS

$Ûy(y∈Y∧<x,y>∈R∧<y,z>∈S)

Û $y(y∈Y∧<z,y>∈S ^C∧<y,x>∈R ^C)

Û<z,x>ÎS ^C oR ^C 所以 (RoS) ^C = S ^CoR ^C 。

33.答案： 证明

充分性: 已知 R ^C =R (证出R对称)

任取x,yÎA 设<x,y>ÎR,则<y,x>ÎR ^C,而R ^C =R 。所以有<y,x>ÎR ，所以R对称。

必要性: 已知R 对称，(证出R ^C =R)

先证R ^C ÍR，任取<y,x>∈R ^C,则<x,y>ÎR,因R对称所以有<y,x>∈R，所以R ^C ÍR。

再证RÍ R ^C，任取<x,y>ÎR, 因R对称，所以有<y,x>∈R，则<x,y>∈R ^C, 所以RÍR ^C。

最后得R ^C =R 。

34.答案：证明

充分性，已知R∩R ^C ÍI_A，(证出R反对称)

任取x,yÎA 设<x,y>ÎR 且<y,x>∈R，<x,y>ÎR∧<y,x>∈RÛ<x,y>ÎR∧<x,y>∈R ^C，

Û <x,y>ÎR∩R ^C Þ <x,y>Î I_A (因R∩R ^C ÍI_A )

Þx=y 所以R反对称。

必要性，已知R反对称，(证出R∩R ^C Í I_A)

任取<x,y>ÎR∩R ^C

<x,y>ÎR∩R ^C Û<x,y>ÎR∧<x,y>ÎR ^CÛ<x,y>ÎR∧<y,x>ÎRÞx=y (因R反对称)

Þ<x,y>ÎI_A 所以R∩R ^C ÍI_A 。

35.答案：

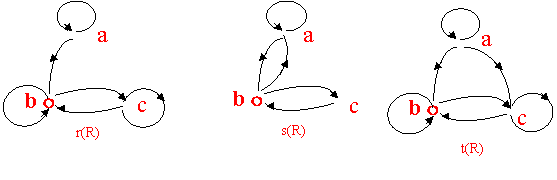
36.答案：

证明：a) r(R2)=R2∪I_AÍR1∪I_A=r(R1),

b) s(R2)= R2∪(R2)^cÍR1∪(R1) ^c =s(R1),

(因为R2 ÍR1 ，所以 (R2) ^c Í(R1) ^c )

c) 因为R2ÍR1，又 R1Ít(R1)， 所以R2Ít(R1) 。于是有t(R2)和 t(R1)都是包含R2的传递关系，而t(R2) 是包含R2的最小的传递关系，所以t(R2) Ít(R1)。

37.答案：

证明： a) r(R1∪R2)= (R1∪R2)∪I_A= (R1∪I_A) ∪(R2∪I_A) =r(R1)∪r(R2) ,

b) s(R1∪R2)= (R1∪R2)∪(R1∪R2) ^c

=(R1∪R2)∪(R1) ^c ∪(R2) ^c c =(R1∪(R1) ^c ) ∪(R2∪(R2) ^c) =s(R1)∪s(R2) ,

c) 因 R1Í (R1∪R2)且R2Í (R1∪R2)，由有关定理得

t(R1)Ít(R1∪R2), t(R2)Ít(R1∪R2)，所以有 t(R1)∪t(R2) Í t(R1∪R2)。

38.答案：A1, A2 ,A3 ,A4 是覆盖。

A1, A2 ,A3也是划分。

A1是最小划分, A2是最大划分。

39.答案：有15个划分。

A1={{1},{2},{3},{4}},

A2={{1},{2,3,4}}, A3={{2},{1,3,4}}, A4={{3},{1,2,3}},

A5={{4},{1,2,3}}, A6={{1,2},{3,4}}, A7={{1,3},{2,4}}, A8={{1,4},{2,3}},

A9={{1},{2},{3,4}}, A10={{1},{3},{2,4}}, A11={{1},{4},{2,3}},

A12={{2},{3},{1,4}} ,A13={{2},{4},{1,3}} , A14={{3},{4},{1,2}}

A15={{12,3,4}}

40.答案：

1．

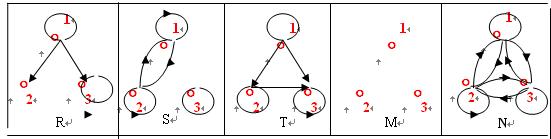
2．

	自反的	反自反	对称的	反对称	传递的
R	×	×	×	√	√
S	√	×	√	×	√
T	√	×	×	√	√
M	×	√	√	√	√
N	√	×	√	×	√

3．等价关系有S和N。

A/S={{1,2},{3}} A/N={{1,2,3}}

偏序有T。哈斯图如下：

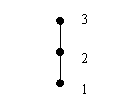
A的极小元、最小元、下界都是1。A的极大元、最大元、上界都是3。

4．RoS＝{<1,1>,<1,2>,<1,3>,<3,3>}

t(R)= {<1,1>,<1,2>,<1,3>,<2,2>,<3,3>}

41.答案：

1． ~R₄＝{<1,3>,<2,4>,<3,1>}

R₂^c＝{<2,1>,<4,2>,<1,4>,<3,3>}

~R₄oR₂^c＝{<1,3>,<2,2>,<3,4>}

s(R₂)＝{<1,2>,<2,4>,<4,1>,<3,3>,<2,1>,<4,2>,<1,4>}

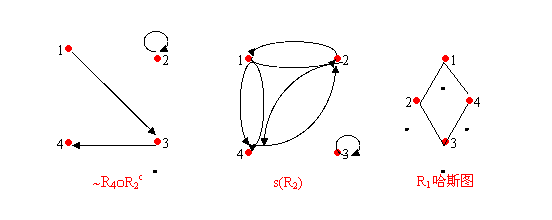
2．

	自反的	反自反的	对称的	反对称的	传递的
R1	∨	×	×	∨	∨
R2	×	×	×	∨	×
R3	∨	×	∨	×	∨
R4	∨	×	×	×	×

3． R₃是等价关系。R₁,是偏序关系。

A/ R₃ ={{1},{2,3,4}}

R₁的哈斯图如上面图所示。

{2,4}的极小元、最小元、和下界都是3，极大元、最大元、上界都是1。

42.答案：.a) c) d) f)不是等价关系。 请看下面反例：

a) R和S都是A上等价关系，R∪S不传递，因而不是等价关系。

c) R是A上等价关系，~R不自反、不传递，因而不是等价关系。

d) R’ 和S都是A上等价关系，R’－S不自反、不传递，因而不是等价关系。

f) R’ 和S都是A上等价关系，r(R’-S) 不传递，因而不是等价关系。

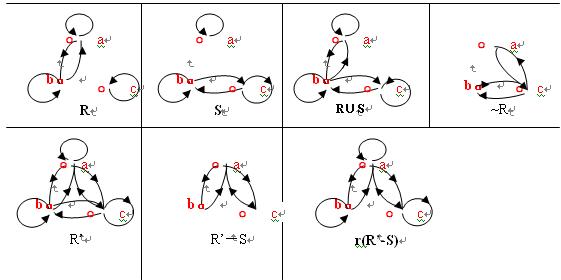
b) 证明R∩S是等价关系。

(1)．证明R∩S的自反性。

任取 x∈A, (证出<x,x>∈R∩S)

因R和S都自反，所以有<x,x>∈R，<x,x>∈S，于是有<x,x>∈R∩S，所以R∩S也自反。

(2)．证明R∩S的对称性：

任取 x,y∈A,设<x,y>∈R∩S, (证出 <y,x>∈R∩S)

则<x,y>∈R，<x,y>∈S，因为R和S对称，所以有<y,x>∈R，<y,x>∈S，于是

<y,x>∈R∩S。∴R∩S对称。

(3)．证明R∩S的传递性：

任取 x,y,z∈A, 设<x,y>∈R∩S,<y,z>∈R∩S, (证出<x,z>∈R∩S)

<x,y>∈R∩S∧<y,z>∈R∩S

Û <x,y>∈R∧<x,y>∈S∧<y,z>∈R∧<y,z>∈S

Û (<x,y>∈R∧<y,z>∈R)∧(<x,y>∈S ∧<y,z>∈S)

Þ <x,z>∈R∧<x,z>∈S （因为R、S传递）

Û <x,z>∈R∩S 所以R∩S传递。

由(1)(2)(3)得R∩S是等价关系。

e).证明R²是等价关系。

(1) 证R²自反，任取a∈A，因为R自反，所以<a,a>∈R，根据关系的复合得，

<a,a>∈RoR, 即<a,a>∈R²，所以R²自反。

(2) 证R²对称， (R²) ^c =( R^c) ²= R² (由R对称得R^c=R) 所以R²对称。

(3) 证R²传递，任取a,b,c∈A,设有<a,b>∈R²,<b,c>∈R²，根据关系的复合得，

($d∈A∧<a,d>∈R∧<d,b>∈R)∧($e∈A∧<b,e>∈R∧<e,c>∈R) ,由于R传递,所以有

<a,b>∈R,<b,c>∈R, ∴<a,c>∈R²。所以R²传递。

最后得R²是等价关系。

43.答案：证明：

a) 证S自反：任取a∈A，∵R是自反的，∴有<a,a>∈R,由S定义得<a,a>∈S, (S定义中c就是a)∴ S自反。

b) 证S对称： 任取a,b∈A，且有<a,b>∈S，由S定义得$c∈A∧<a,c>∈R∧<c,b>∈R，由R对称得 $c∈A∧<b,c>∈R∧<c,a>∈R，由S定义得<b,a>∈S，所以S对称。

c)证S传递：任取a,b,c∈A，有<a,b>∈S,<b,c>∈S，由S定义得

($d∈A∧<a,d>∈R∧<d,b>∈R)∧($e∈A∧<b,e>∈R∧<e,c>∈R) ,

由于R传递，所以有<a,b>∈R,<b,c>∈R，由S定义得<a,c>∈S, 所以S传递。

综上所述得S是A上等价关系。

44.答案：证明：:任取a∈A，有已知得$b∈A，,使得<a,b>∈R，由R对称得<b,a>∈R,又由R传递得， <a,a>∈R，所以,R自反。 因此R是等价关系。

45.答案：

1．证明R是A×A上等价关系。

.(1) 证R的自反性。

任取<a,b>∈A×A，因为a+b=b+a , 由R定义得<a,b>R<a,b>, 所以R自反。

(2)证明对称性

任取<a,b>,<c,d>∈A×A，设有<a,b>R<c,d> ，由R定义得a+d=b+c，显然有

c+b=d+a,根据R定义得<c,d> R <a,b>，所以R具有对称性。

(3) 证明传递性

任取<a,b>,<c,d>,<e,f>∈A×A，设有<a,b>R<c,d>和<c,d>R<e,f> ，由R定义得a+d=b+c，c+f=d+e，于是有 a+d+c+f=b+c+d+e 等号两侧分别消去d+c和c+d得, a+f=b+e 由R定义得<a,b>R<e,f>, 所以R具有传递性。

综上所述，R是A×A上等价关系。

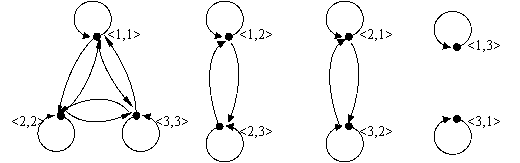
故A×A/R={{<1,1>,<2,2>,<3,3>},{<,1,2>,<2,3>},{<2,1>,<3,2>},{<1,3>},{<3,1>}}

46.答案：

1. 证明E是A上的等价关系。

1).证明E自反：任取xÎA，(推出xEx)

因为R上是A上自反的，所以有xRx, xRxÙxRx,由E定义得xEx,所以E是自反的。

2).证明E对称:任取x,yÎA,且有xEy(推出yEx)。

由E定义xRy∧yRx，当然有yRx∧xRy，由E定义得yEx， 所以E对称。

3).证明E传递:任取x,y,zÎA,且有xEyÙyEz (推出xEz)。

由E定义得 (xRy∧yRx)Ù(yRz∧zRy)

Û(xRy∧yRz)Ù(zRy∧yRx)ÞxRz∧zRx (因为R传递)

ÛxEz 所以E传递。最后得E是A上等价关系。

2．证S是A/E上的偏序关系：

1).证明S自反：任取[x]_E ÎA/E，(推出[x]_ES[x]_E)

于是得xÎA，因R上是A上自反的，所以有xRx，又由S定义得，[x]_ES[x]_E，

所以S自反。

2).证明S反对称：任取[x]_E, [y]_E∈A/E，设有[x]_E S[y]_E和[y]_E S[x]_E,，(推出[x]_E =[y]_E)

由S定义得xRy和yRx，再由E定义得:xEy,由等价类性质得[x]_E =[y]_E，所以S反对称。

3).证明S传递：任取[x]_E, [y]_E, [z]_E∈A/E, 设有[x]_E S [y]_E Ù[y]_E S [z]_E , (推出[x]_ES[z]_E ),

[x]_E S[y]_E Ù[y]_ES [z]_E ÛxRyÙyRzÞxRz (因R传递)

Û[x]_E S[z]_E ,所以S传递。

最后得S是A/E上偏序关系。

47.答案：证明：

先证明 [a]=[b] 当且仅当 <a,b>∈R。

充分性：若<a,b>∈R，则任何x∈[a]，有<a,x>∈R，由对称性得<b,a>∈R，再由传递性得<b,x>∈R,∴x∈[b]，所以[a]Í[b]。 类似可证[b]Í[a]。∴ [a]=[b]。

必要性：如果[a]=[b]，由于有aRa，所以a∈[a]，a∈[b]，所以有<b,a>∈R，由对称性得<a,b>∈R.

再证明 [a]∩[b]≠Φ， 当且仅当 <a,b>∈R。

充分性：如果<a,b>∈R, 假设[a]∩[b]=Φ。由等价类定义得b∈[a]。又由bRb，所以

b∈[b]。∴b∈[a]∧x∈[b], 与[a]∩[b]=Φ, 产生矛盾。所以必有[a]∩[b]≠Φ。

必要性：如果[a]∩[b]≠Φ，则存在x∈[a]∩[b], 所以x∈[a]∧x∈[b], 所以<a,x>∈R , <b,x>∈R,由R对称得<x,b>∈R, 由传递得<a,b>∈R。

综上所述，aRb 、[a]=[b] 与 [a]∩[b]≠Φ 彼此等价。

48.答案：这样的二元关系有6个。所对应的商集如下：

A1={{1},{2},{3,4}}, A2={{1},{3},{2,4}}, A3={{1},{4},{2,3}},

A4={{2},{3},{1,4}} ,A5={{2},{4},{1,3}} A6={{3},{4},{1,2}}

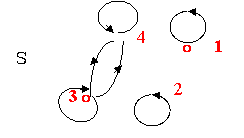
A1所对应的等价关系S如上图所示。

49.答案：

1。

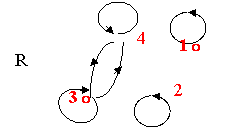
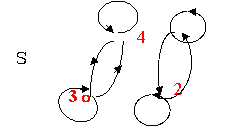
50.答案：tsr(R)＝{<1,1>,<1.2>,<2,4>.<2,2>,<3,3>,<4,4>,<2,1>,<42>,<1,4>,<4,1>}。

tsr(R)的有向图如下。从此图看出，tsr(R)有自反、对称和传递性质。所以它是等价关系。

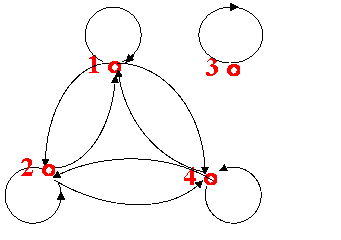
商集A/tsr(R)＝{{1,2,4},{3}}。

51.答案：首先证明R对称。

R^C=(RοR^C) ^C =RοR^C= R 所以R对称。

再证明R传递。

任取a,b,c∈A,设有<a,b>∈R,<b,c>∈R，根据关系的复合得，<a,c>∈RοR，因为

R对称，则R^C= R，于是<a,c>∈RοR^C, 而RοR^C= R 所以 <a,c>∈R，所以R传递。

由已知R自反，最后得R是等价关系。

52.答案：

1．真值为真。

因为s(R)是对称的，根据闭包的性质得，rs(R)是自反和对称的。再根据闭包的性质得，trs(R) 是传递、自反和对称的，所以trs(R)是A上的等价关系。

2．真值为假。因为R是A上的对称和传递的二元关系，则由于下面命题公式

"x"y((xÎAÙyÎAÙ< x,y >ÎRÙ< y,x >ÎR) ®< x,x > ÎR) 真值为真时，不一定得出R是自反的。因为这个x不一定是A中任何一个。请看下面反例，下面关系R就是对称、传递，但不是自反的。

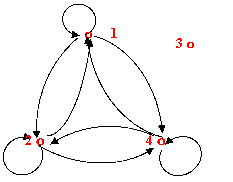
3．真值为假。因为谓词公式Ø$x$y(xÎAÙyÎAÙ< x,y >ÎRÙ< y,x >ÎR) 在论域A上为真，

不是R为反对称的必要条件。

举反例：A={1,2},恒等关系I_A={<1,1>,<2,2>} 不满足上面谓词公式，但它是反对称的。

MR=

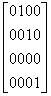
53.答案：根据矩阵得 R＝{<1,2>,<2,3>,<4,4>}

s(R)＝{<1,2>,<2.3>,<4,4>.<2,1>,<3,2>,<4,4>}。

ts(R)＝{<1,2>,<2.3>,<4,4>.<2,1>,<3,2>,<4,4>,<1,3>,<3,1>,<1,1>,<2,2>,<3,3>}

ts(R)的有向图如下：

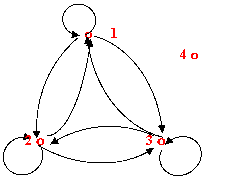
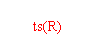
可见它是等价关系，且商集 A/ts(R)＝{{1,2,3},{4}}.

54.答案：A：⑻；B：⑸；C：Φ。

55.答案：

1．用R(a)来定义R有自反性：任取x∈A，都有x∈R(x)。

用R(a)来定义R反自反性：任取x∈A，都有xÏR(x)。

用R(a)来定义R、对称性：任取x∈A，y∈A，如果有y∈R(x)，则也有x∈R(y)。

用R(a)来定义R反对称性：任取x∈A，y∈A，且x¹y，则如果有y∈R(x)，则也有xÏR(y)。

用R(a)来定义R传递性：任取x∈A，y∈A，z∈A，如果有y∈R(x)。又有z∈R(y)，

则也有z∈R(x)。

2．如果R是A上的等价关系，则R(a)就是a相对R的等价类。于是

商集A/R＝{R(a)|a∈A}

56.答案：证明：

(1) 充分性：已知R(a)=R(b)，

假设<a,b>ÏR，由R(a)定义得，bÏR(a)，而由于R是等价关系，所以有<b,b>∈R，于是b∈R(b)，由已知得b∈R(a)，与bÏR(a)矛盾。所以必有<a,b>∈R。

(2) 必要性：已知<a,b>∈R，

先证明R(a) ÍR(b)。任取x∈R(a)，由R(a)定义得<a,x>∈R；又由R对称得<b,a>∈R；再根据R传递得<b,x>∈R，所以x∈R(b)，故R(a) ÍR(b)。

再证明R(b)Í R(a)。任取x∈R(b)，由R(b)定义得<b,x>∈R；再根据R传递得<a,x>∈R，所以x∈R(a)，故R(b) ÍR(a)。

最后得R(a)=R(b)

最后得：R是等价关系时，<a,b>∈R，当且仅当R(a)=R(b)。

57.答案： A/R∩S＝{{a,c},{b},{d},{e,f,g}}。

58.答案：首先证明R对称。

R^C=(RοR^C) ^C =RοR^C= R 所以R对称。

再证明R传递。

任取a,b,c∈A,设有<a,b>∈R,<b,c>∈R，根据关系的复合得，<a,c>∈RοR，因为

R对称，则R^C= R，于是<a,c>∈RοR^C, 而RοR^C= R 所以 <a,c>∈R，所以R传递。

最后证明R自反。

因为对任何aÎA，存在bÎA，使得<a,b>ÎR，由对称性得<b,a>ÎR，再由传递性得

<a,a>ÎR，所以R自反。

最后得R是等价关系。

59.答案：

1．证明RοR是等价关系。

(1) 证RοR自反，任取a∈A，因为R自反，所以<a,a>∈R，根据关系的复合得，

<a,a>∈RoR, 所以R²自反。

(2) 证RοR对称，(RοR) ^c= R ^cοR^c = RοR (由R对称得R^c=R) 所以RοR对称。

(3) 证RοR传递，任取a,b,c∈A,设有<a,b>∈RοR,<b,c>∈RοR，根据关系的复合得，

($d∈A∧<a,d>∈R∧<d,b>∈R)∧($e∈A∧<b,e>∈R∧<e,c>∈R) ,由于R传递,所以有

<a,b>∈R,<b,c>∈R, ∴<a,c>∈RοR。所以RοR传递。

最后得RοR是等价关系。

2． 计算RοR＝{<1,1>,<1.2>,<2,2>.<2,1>,<3,3>}

A/RοR.＝{{1,2},{3}}。

60.答案：解.1.关系R的有向图.

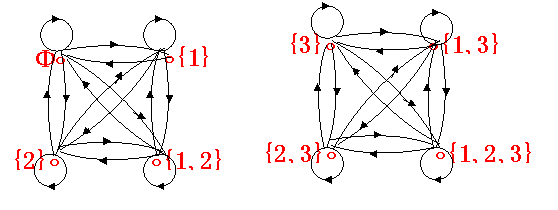
2. 从R有向图看出R有自反,对称和传递性,故是等价关系

P(X)/R={{F,{1},{2},{1,2}},{{3},{1,3},{2,3},{1,2,3}}}

61.答案：因为R是等价关系，具有自反、对称和传递性，所以根据闭包的性质，得

(R⁺∪I_A)^*∪tsr(R∩R^c)＝(R⁺∪I_A)^*∪tsrR (因为R对称，R＝R^c 所以R∩R^c＝R)

＝(R⁺∪I_A)^*∪ts(R) (因为R自反，所以r(R)＝R)

＝(R⁺∪I_A)^*∪t(R) (因为R对称，所以s(R)= R)

＝(R⁺∪I_A)^*∪R (因为R传递 ，所以 t(R)＝R)

＝(R∪I_A)^*∪R (因为R传递 ，所以 R⁺＝t(R)＝R )

＝R^*∪R (因为R自反，所以R∪I_A＝R)

＝R∪R (因为R自反，传递 所以R^*＝tr(R)＝R )

＝R

62.答案：解：

1. A/ R₁ÇR₂ ＝{{a,c},{b},{d},{e,f,g}}

2. [x]_R1ÇR2=[x]_R1Ç[x]_R2 。

证明：先证明 [x]_R1ÇR2Í [x]_R1Ç[x]_R2

任取y∈[x]_R1ÇR2，由等价类定义得<x,y>∈R₁ÇR₂ 所以<x,y>∈R₁ 且<x,y>∈R₂，于是y∈[x]_R1 y∈[x]_R2 所以y∈[x]_R1Ç[x]_R2 故 [x]_R1ÇR2Í [x]_R1Ç[x]_R2 。

再证明 [x]_R1Ç[x]_R2Í[x]_R1ÇR2

任取y∈x]_R1Ç[x]_R2，于是y∈[x]_R1 y∈[x]_R2 所以<x,y>∈R₁ 且<x,y>∈R₂，所以<x,y>∈R₁ÇR₂，由等价类定义得y∈x]_R1Ç[x]_R2，所以有 [x]_R1Ç[x]_R2Í[x]_R1ÇR2

最后得：[x]_R1ÇR2=[x]_R1Ç[x]_R2 。

63.答案：A/R₁∩R₂＝{{a,c},{b},{d},{e,f,g}} R₁∩R₂有向图如下：

64.答案：Cr(A)＝{{1,2,5},{1,4,5},{2,3},{3,4}}

65.答案：首先根据矩阵画出r的简化图如下：

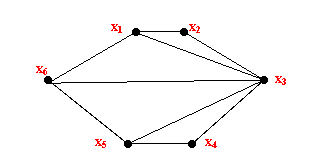
完全覆盖 Cr(X)={{x1,x2,x3,},{x1,x3,x6},{x3,x4,x5},{x3,x5,x6}}

66.答案：解.先画出r的简化图, 如下图所示：

3o

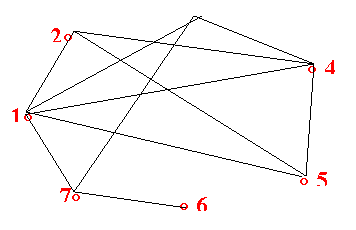
于是得完全覆盖为:

Cr(X)={{1,2,4,5},{1,3,7},{1,3,4},{7,6}}

67.答案：

1．证明R自反：任取x∈A，因为x可以被x整除，所以<x,x>∈R，故R自反。

2．证明R反对称：任取x,y∈A,设<x,y>∈R, < y, x >∈R，(要证出 x= y )

由R定义得 x可被y整除, 即x =ny (n∈A)；y可被x整除， 即y =mx (m∈A)，于是有x ＝ny＝nmx ，因为m和n都是整数，必有nm＝1，所以x=y，故R是反对称的。

3．证R传递性：任取x,y,z∈A，设xRy, yRz, (要证出xRz)

由R定义得 x可被y整除, 即x =ny (n∈A)；y可被z整除， 即y =mz (m∈A)，于是有x＝ny＝nmz ，因为m和n都是整数，nm也是整数，于是 x可被z整除， 所以有xRz, 所以R传递。

所以R是A上的偏序关系。 证毕

68.答案：1. <A,≤>，<B,≤>的有向图如下：

69.答案：1. <C,≤>，<D,≤>的有向图如下：

2．

	极小元	极大元	最小元	最大元	上界	下界	上确界	下确界
{2,3}	2,3	2,3	无	无	6,12,24,36	1	6	1
{6,12,24}	6	24	6	24	24	1,2,3,6	24	6

70.答案：

1．(1) 证明R自反：任取x∈F，因为x是x的前缀，所以有<x,x>∈R，故R自反。

(2) 证明R反对称：任取x,y∈F，设<x,y>∈R, < y, x >∈R，(要证出 x= y )

由R定义得 x是y的前缀, 不妨设y =xα (α∈F)，y是x的前缀, 不妨设x =yβ (β∈F)；

于是 x = yβ＝xαβ，可见α＝β＝λ，即x= y。

(3) 证R传递性：任取x,y,z∈F，设<x,y>∈R, <y,z>∈R, (要证出<x,z>∈R)

由R定义得 x是y的前缀, 不妨设y =xα (α∈F)，y是z的前缀，不妨设z =yβ (β∈F)；于是 z = yβ＝xαβ，可见x是z的前缀。所以有 <x,z>∈R，故R传递性。

最后得，R是F上的偏序关系。

2．R的哈斯图如下：

3．F的极小元是λ 。无最大元。

71.答案：

子 集	极小元	极大元	最小元	最大元	上界	下界	上确界	下确界
{x3, x4 ,x5}	x4, x5	x3	无	x3	x1, x3	无	x3	无
{x1,x2, x3}	x2, x3	x1	无	x1	x1	x4	x1	x4
{x2,x3, x4}	x4	x2, x3	x4	无	x1	x4	x1	x4
P	x4, x5	x1	无	x1	x1	无	x1	无

72.答案： ~R的有向图如下：

°4

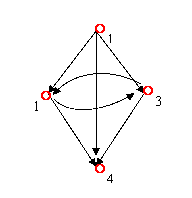
73.答案：1．集合A的极大元：a,c；极小元：f；最小元：f；最大元：没有。

2．子集{b,f}的上界：a，c；下界：f 。

3．偏序关系≤的关系图如下：

．
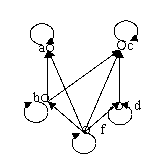