第五章
习题
第一节 概率的计算 (33)
单选题
1. 某人忘记了电话号码的最后一位数字，因而他随意拨号，第一次接通电话的概率是：
A、1/9 B、1/
2. 某福利中心为了筹集急救资金，发行了一次有奖彩票，共10万张，其中有奖的2万张，特别的，一等奖有2张奖金1万元，假设有奖与无奖彩票是均匀混合随机发放的，那么小张买一张彩票中一等奖的概率是多少？
A、1/100000 B、2/
3. 某人因听说飞机失事的报道而不敢乘坐飞机外出办事，其同事帮找来近三年的飞行记录，其中安全飞行记录共有15万次左右，而失事纪录只有2次，此人了解后便不再害怕乘坐飞机，因为他算出一次飞行中飞机失事的概率：
A、约为1/75000 B、精确等于1/
4. 一次事件(不可重复)的概率叫做：
A．客观概率 B. 条件概率 C. 相对频数 D. 主观概率
5. 火星上有生命的概率为0.0001，其中这里的“概率”指的是：
A．某系统的内部特性 B. 条件概率 C. 主观概率
D. 相对频数
6. 某一居民区有500户人家装有电话。某天晚上恰有100户家中无人，而在其余400户中，又有120户人家拒绝电话调查。如果随机地给这些家庭中的某一家打电话，试求电话打到有人的家庭，但这家人却拒绝调查的概率：
A．6/25
B．4/
7. 设某地有甲、乙两种杂志，该地成年人中有20％读甲杂志，16％读乙杂志，8％兼读甲和乙两种杂志。问成年人中百分之几至少读一种杂志？
A．20% B.36%
C.24% D. 28%
8. 袋中有5个白球 ，n个红球，从中任取一个恰为红球的概率为2/3，则n为：
A、16 B、
9. 连掷两次骰子，它们的点数和是4的概率是：
A．1/36 B. 1/
10.
连掷两次骰子，它们的点数都是4的概率是：
A．1/36 B. 1/
11.
独立地抛掷一枚质量均匀硬币，已知连续出现了 10 次反面，问下一次抛掷时出现的是正面的概率是：
A．1/11 B. 1/
12.
甲、乙两人各自投篮的命中率分别为0.8和0.7,假设两人互不影响,则甲、乙两人都投中的概率是：
A．0.56 B.
13.
一个袋中装有两个红球三个白球，第一次摸出一个红球又放回，再任意摸出一个，则第二次摸到白球的概率为：
A．3/4 B. 3/
14.
“有志者，事竟成”可以用概率论中的一个结论来近似解释，这个结论是：
A．概率是某系统内部的特性
B. 大量重复实验中频率接近与概率
C. 一次实验中小概率事件不可能发生
D. 小概率事件必然发生
15.
在风险和利益之间寻求平衡的过程叫做：
A．概率分析 B. 决策分析 C. 统计推断 D. 统计分析
16.
某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用。单独采用甲、乙预防措施所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少。
（总费用=采取预防措施的费用+发生突发事件损失的期望值.）
A．不采取预防措施
B. 单独采取措施甲
C. 单独采取预防措施乙
D. 联合采取甲、乙两种预防措施
多选题
1. 概率可通过下列那些办法计算得到：
A．利用等可能性 B. 相对频数 C.主观概率
D.几何概率中的面积比
2. 下列事件中指的是主观概率的有：
A． Jerry投掷一枚质量不均匀的硬币1000次得到200次正面向上，因此他认为在一次投掷中，这枚硬币正面向上的概率为1/5
B. Tom同学觉得这次统计课期末考试他及格的概率为1/2
C. 某游客认为这次旅行平安到达的概率为9999/10000
D. 某球迷认为这次世界杯中法国队胜出的概率为4/5
3. 对于事件A、B，它们至少有一个发生的概率是
P(A)+P(B) ，则A、B应满足：
A．A发生时B肯定不发生 B. B发生时A 肯定不发生
C. A、B相互不影响
D. A、B不同时发生
4. 甲、乙两人独立地解同一问题，甲解决这个问题的概率是p1，乙解决这个问题的概率是p2，那么恰好有1人解决这个问题的概率是：
A． p1 p2 B． p1(1－p2)+
p2 (1－p1)
C． 1－p1 p2 D． 1－(1－p1) (1－p2)－p1
p2
5. 为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率（记为P）和所需费用如下表5.1：
表5.1
|
预防措施 |
甲 |
乙 |
丙 |
丁 |
|
P |
0.9 |
0.8 |
0.7 |
0.6 |
|
费用（万元） |
90 |
60 |
30 |
10 |
预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超过120万元，且使得此突发事件不发生的概率大于等于0.9的前提下，下列那些预防方案是可行的：
A．方案1：单独采用甲措施
B．方案2：联合采用甲、乙两种预防措施
C．方案3：联合采用甲、丁两种预防措施
D．方案4：联合采用三种预防措施
判断题
1.
概率是－1～1之间的一个数，它告诉了我们一件事发生的经常度。
2.
在重复实验中，一个特殊结果出现的可能性为多少，可以用概率来回答。
3.
任何情况都可以利用等可能性来计算概率。
4.
利用等可能性计算概率需满足的条件是，实验的所有可能结果数是已知的，且每种实验结果出现的可能性一样。
5. 利用一个随机事件的频率(比例)能够求出概率的一个精确值。
6.
甲、乙二人做如下的游戏：从编号为1到20的卡片中任意抽出一张，若抽到的数字是奇数，则甲获胜，否则乙获胜，这个游戏对甲、乙双方是公平的。
7.
甲、乙二人做如下的游戏：从编号为1到20的卡片中任意抽出一张，若抽到的数字是3的倍数，则甲获胜；若抽到的数字是5的倍数，则乙获胜，此时这个游戏对甲、乙双方是公平的。
8. 主观概率指的是对于不能做重复试验的随机事件，人们各自给出的对这个事件发生的相信程度。
9. 小概率事件指的就是不可能发生的事件。
10.
小概率事件在一次实验中能够认为不会发生，飞机失事就是小概率事件，虽然乘坐飞机有危险，但是人们还是会乘坐飞机旅行。
11.
小概率事件必然发生，指的是在无穷次实验中，小概率事件肯定会发生。对
12.
设某件事件发生的概率为p，乘积p(1－p)能衡量此事件发生的不确定性，特别得，当p＝0.5时，不确定性最大。
第二节 离散变量的概率分布 (28)
单选题
1.
每张奖券中末等奖的概率为1/10,某人购买了20张号码杂乱的奖券,设中末等奖的张数为X，则X 服从：
A．二项分布 B.泊松分布 C.正态分布 D.超几何分布
2.
一年内飞机失事的次数可以看成服从：
A．二项分布
B. 泊松分布 C. 正态分布 D. 超几何分布
3. 假如盒子里有a个黑球与b个白球，任意有放回和不放回取出 m 个；那么这 m 个小球中含有黑球的数目分别服从：
A．超几何分布、二项分布 B.超几何分布、泊松分布
C. 二项分布、 超几何分布 D.二项分布、正态分布
4. 如果一个事件每次发生的概率是p，那么在 n 次观察中能够看到这个事件出现 k 次的概率是：
A．
B. 
C. 
D. 
5.
具有概率分布
的是下列那个分布：
A．超几何分布
B．正态分布 C．二项分布 D．泊松分布
6.
具有概率分布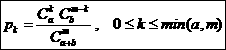
的是下列那个分布：
A．正态分布
B．超几何分布 C．二项分布 D．泊松分布
7.
设某课堂考卷上有20道选择题，每题答案是4选1，某学生只会做10题，另外10题完全不会，于是就瞎猜，求他能猜对5题的概率。
A．
B.
C.
D.
8.
设某课堂考卷上有20道选择题，每题答案是4选1，某学生只会做10题，另外10题完全不会，于是就瞎猜，求他至少能猜对5题的概率。
A．
B.
C. 
D. 
9.
在有5张记有1、2、3、4、5的卡片中，现无放回的抽取两次，一次一张，则第二次取到奇数卡的概率为：
A．4/25 B. 3/
10.
在有5张记有1、2、3、4、5的卡片中，现无放回的抽取两次，一次一张，则两次都取到奇数卡的概率分别为：
A．1/2 B. 3/
11.
从1，2，……，9这九个数中，随机抽取2个不同的数，则这2个数的和为奇数的概率是：
A．1/2 B. 15/
12.
每次试验的成功率为p(0<p<1)，则在3次重复试验中至少失败一次概率为：
A．
(1－p)2
B. 1－p2
C. 3 (1－p)
D. 1－p3
13.
事件A发生的概率p＝1/3，则在15次实验中，下列事件那个概率最大？
A．A发生15次 B. A发生5次 C. A发生10次 D. A发生7次
14.
某商场每月销售某商品的数量服从参数为3的泊松分布，则下月该商场买出5件该产品的概率为：
A．
B. 
C. 
D. 
多选题
1．下列那些分布是属于离散变量的概率分布：
A．二项分布 B. 泊松分布 C. 正态分布 D. 超几何分布
2. 关于二项分布下列说法正确的是：
A．如果一个事件每次发生的概率是1/2，那么在n次实验中这个事件至少出现 k 次的概率与n－k次的概率一样大
B. 如果一个事件每次发生的概率是p，那么在n次实验中这个事件至少出现 k 次的概率与n－k次的概率一样大
C. 如果一个事件每次发生的概率是p，那么在n次观察中能够看到这个事件至多出现 k 次的概率是：
D. 如果一个事件每次发生的概率是p，那么在n次观察中能够看到这个事件至少出现 k 次的概率是：
3. 某书第一节课后有习题10道，为判断题，某学生都不会做，于是就瞎猜，则他至少能猜对5题的概率为：
A．
B.
C. 
D. 
4. 有放回抽样的特点是：
A. 各次抽选互不影响
B. 各次抽选相互影响
C. 每次抽选时，总体的大小逐渐减少
D. 每次抽选时，总体的大小始终不变
E. 每个个体被抽中的机会在各次抽选中相等
5. 每年袭击某地的台风次数近似服从参数为4的泊松分布。则一年中该地区受台风袭击次数为3～5的概率为：
A．
B. 
C. 
D. 
判断题
1. 抛一个质量均匀的硬币10次，则出现8次正面的概率大于2次正面的概率。
2. 抛一个质量均匀的硬币10次，则出现7次正面的概率大于2次正面的概率。
3.
抛一个质量均匀的硬币n次，正面出现n/2次的概率最大。
4. 抛一个质量均匀的硬币n次，当n为偶数时，正面出现n/2次的概率最大。
5. 抛一个质量均匀的硬币n次，当n为奇数时，正面出现(n+1)/2和(n-1)/2次的概率最大。
6. 泊松分布的背景指的是稀有事件发生的次数，这个次数可以是无穷多次。
7. 当样本量很大时超几何分布可以用二项分布近似。
8. 样本量较小时，二项分布可以用正态分布近似。
9. 泊松分布可以看做是二项分布的特例。
第三节 连续变量的概率分布 (18)
单选题
1.
某大学为学生体检，测量了学生身高体重等基本信息，请问所有学生的身高可以看做服从：
A．二项分布 B. 卡方分布 C. 正态分布 D. t分布
2.
某大学为学生体检，测量了学生身高体重等基本信息，若任取一个寝室的8名同学，那么这8名同学的身高可以看做服从：
A．二项分布 B. 卡方分布 C. 正态分布 D. t分布
3.
服从标准正态分布的变量的均值与标准差分别是：
A．0，0 B. 0，
4.
X 服从正态分布N(4，25)，下面哪个随机变量服从标准正态分布N (0,1) ？
A．(X- 2 ) / 25 B. (X- 2) /
5.
由某机器生产的螺栓的长度(cm)服从参数m＝10.05, s=0.06的正态分布。
现取一螺栓其长度为10.17，将这个长度转换为标准z得分是：
A．2 B.
6. 已知标准z变量取值在-1.96～1.96之间的概率为0.95。在一次公务员资格考试中，甲同学考了80分，可以认为此次考试成绩服从正态分布，平均成绩是 60分，标准差是10分，则可以认为：
A．有等于5％的同学能比他考得更好
B. 有等于2.5％的同学能比他考得更好
C. 有少于2.5％的同学能比他考得更好
D. 有2.5％～5％的同学能比他考得更好
7.
服从自由度为n的t分布的变量的均值是：
A．0 B. n
多选题
1.
下列那些分布是属于连续变量的概率分布：
A．正态分布
B. 卡方分布 C. t分布 D. F分布
2.
下列那些分布是有一族的：
A．正态分布
B. 卡方分布 C. t分布 D. F分布
3. 关于标准正态分布曲线下列说法正确的是：
A．关于直线x=0对称
B. 关于直线x=1对称
C. 是一个钟型曲线
D. 曲线下面的面积等于1
4. 下列关于t分布说法正确的是：
A．t分布有一族
B. t分布的曲线关于y轴对称
C. 服从t分布的变量的标准差等于1
D. t分布适用于小样本的情况
5. 下列关于正态分布的曲线与t分布的曲线说法正确的是：
A．正态分布的曲线与t分布的曲线基本形状相同
B. 正态分布曲线的中部较高
C. 它们都关于直线x=0对称
D. t分布曲线在其均值周围的聚集程度比正态分布要差一些
6. 下列关于卡方分布说法正确的是：
A．卡方分布有一族
B. 卡方分布的曲线关于y轴对称
C. 卡方分布的曲线不是对称的
D. 卡方分布的取值都大于等于零
7. 下列关于F分布说法正确的是：
A．F分布有一族
B. F分布的曲线关于y轴对称
C. F分布有两个自由度
D. F分布的取值都大于等于零
判断题
1．服从正态分布的变量的均值为0，标准差为1。
2. 如果变量X服从均值是m，标准差是s的正态分布，则z=(X－m)/s 服从标准正态分布。
3. t分布的曲线与F分布的曲线都关于y轴对称。
4. 当t分布的自由度比较大(超过45)时，t分布就近似于标准正态分布。
参考答案
第一节 概率的计算 (33)
单选题
1.B
2.C 3.A 4.D
5.C 6.A 7.D
8.B 9.D 10.A 11. C 12.A 13.B 14.D 15.B 16.D
多选题
1.ABCD 2.BCD 3.ABD 4.BD 5.AC
判断题
13. 错
14. 对
15. 错
16. 对
17. 错
18. 对
19. 错
20.
对
21.
错
22.
对
23.
对
24.
对
第二节 离散变量的概率分布 (28)
单选题
1.A
2.B 3.C 4.A
5.D 6.B 7.A 8.C
9.B 10.D 11.C 12.D 13.B 14.A
多选题
1．ABD
2. AC
3.CD
4. ADE
5. BCD
判断题
10.
错
11.
对
12.
错
13.
对
14.
对
15.
对
16.
对
17.
错
18.
对
第三节 连续变量的概率分布 (18)
单选题
1.C 2.D 3.B
4.D 5.A 6.C 7.A
多选题
1.ABCD 2.BCD 3.ACD 4.ABD 5.ABCD 6.ACD 7.ACD
判断题
1． 错
2. 对
3.
错
4. 对